Dy dx -Fotos und -Bildmaterial in hoher Auflösung

Mechanik der engineeringComprising Statik und Dynamik von Festkörpern: und die Mechanik der Werkstoffe von Konstruktionen oder Festigkeit und Elastizität der Träger, Säulen, Bögen, Wellen, etc. Abb. 282. 330 MECHANIK VON ENGINEERING. Die Tangente an 0 als horizontale wir für x = 0, j = 0,.-. (7 = 0. Aber da die Tangente bei C ist auch hori-zontal, können wir für x-l, dy + dx = 0 und erhalten 0 = - % WP+m+j4 wP; woher M0=LJVl (3) Als Zeitpunkt des Stress-conple in der Nähe der Wand bei 0 und bei C, Abb. 283, die Gleichung der moment Kurve (in einer Dosis stetige Kurve in diesem Fall) wird von Putti gefunden Stockfoto

RM2ANF319–Mechanik der engineeringComprising Statik und Dynamik von Festkörpern: und die Mechanik der Werkstoffe von Konstruktionen oder Festigkeit und Elastizität der Träger, Säulen, Bögen, Wellen, etc. Abb. 282. 330 MECHANIK VON ENGINEERING. Die Tangente an 0 als horizontale wir für x = 0, j = 0,.-. (7 = 0. Aber da die Tangente bei C ist auch hori-zontal, können wir für x-l, dy + dx = 0 und erhalten 0 = - % WP+m+j4 wP; woher M0=LJVl (3) Als Zeitpunkt des Stress-conple in der Nähe der Wand bei 0 und bei C, Abb. 283, die Gleichung der moment Kurve (in einer Dosis stetige Kurve in diesem Fall) wird von Putti gefunden

Archiv Bild ab Seite 328 der Denkschriften der Kaiserlichen Akademie der. Denkschriften der Kaiserlichen Akademie, Christian/Mathematisch-Naturwissenschaftliche Classe denkschriftender 20 kais Jahr: 1862 Allgemeine Transformation der bestimmten Doppel-Integrale. 155 dann b als positiv, so wird man nach einigen sich leicht anbietenden Reductionen sterben folgende Gleichung erhalten: Ich dx ff (ax'' durch ') dy=/tÃ¤7 H) - ir-r (-+-) m n I ttpÂ " ", "âf" 4 // "âaf n âw 4-âL-j.zm+n f{z) dz I{âtf lt w> dtA-/zm +7'lÃr-z) dzJ (lât) m'Â"'-+'' j Macht man sterben noch speciellere Annahme, Stockfoto

RMW27Y48–Archiv Bild ab Seite 328 der Denkschriften der Kaiserlichen Akademie der. Denkschriften der Kaiserlichen Akademie, Christian/Mathematisch-Naturwissenschaftliche Classe denkschriftender 20 kais Jahr: 1862 Allgemeine Transformation der bestimmten Doppel-Integrale. 155 dann b als positiv, so wird man nach einigen sich leicht anbietenden Reductionen sterben folgende Gleichung erhalten: Ich dx ff (ax'' durch ') dy=/tÃ¤7 H) - ir-r (-+-) m n I ttpÂ " ", "âf" 4 // "âaf n âw 4-âL-j.zm+n f{z) dz I{âtf lt w> dtA-/zm +7'lÃr-z) dzJ (lât) m'Â"'-+'' j Macht man sterben noch speciellere Annahme,

. Frühe geophysikalische Papiere der Gesellschaft der Exploration Geophysicists. Abb. i, dass die Tangente in P in jeder Kurve auf S durch P in der (x, y)-Ebene liegt. Die Situation bisher beschrieben ist schematisch in Abbildung 1, wo, für die Bequemlichkeit, nur ein Teil der Oberfläche S in der Nähe von P angegeben wird angezeigt. Gleichung des S Nehmen wir an, dass die Gleichung von S, auf das gewählte Koordinatensystem genannt, (i) 2 = z(x,y), und dass dieser Ausdruck ist in Reihe über P erweitert; das ist, (2) z=a+ (px + Qy) - f-^ (Rx 2 + 2 sxy + ty2) + â¢â¢â, wo dz dz ox dz dy dx* d2z dxdy t dy* t Stockfoto

RMMAAW77–. Frühe geophysikalische Papiere der Gesellschaft der Exploration Geophysicists. Abb. i, dass die Tangente in P in jeder Kurve auf S durch P in der (x, y)-Ebene liegt. Die Situation bisher beschrieben ist schematisch in Abbildung 1, wo, für die Bequemlichkeit, nur ein Teil der Oberfläche S in der Nähe von P angegeben wird angezeigt. Gleichung des S Nehmen wir an, dass die Gleichung von S, auf das gewählte Koordinatensystem genannt, (i) 2 = z(x,y), und dass dieser Ausdruck ist in Reihe über P erweitert; das ist, (2) z=a+ (px + Qy) - f-^ (Rx 2 + 2 sxy + ty2) + â¢â¢â, wo dz dz ox dz dy dx* d2z dxdy t dy* t

. Denkschriften der Kaiserlichen Akademie, Christian/Mathematisch-Naturwissenschaftliche Classe. Mathematik, Wissenschaft. Allgemeine Transformation der bestimmten Doppel-Integrale. 155 dann b als positiv, so wird man nach einigen sich leicht anbietenden Reductionen sterben folgende Gleichung erhalten: Ich dx ff (ax'" von") dy=/tÃ¤7 H) - ir-r (-+-) m n i ttpÂ " ", "âf "4 // "âaf n â * w4 - âL-j.zm+n * f{z) dz I{âtf lt w*> dtA-/zm +7'lÃr-z) dzJ (lât) m'Â"' - + "'* j Macht man sterben noch speciellere Annahme, dass Â £ = oo, jy = oo sei, so wird der Mensch haben: O * CO fdx ff (a Stockfoto

RMPFGM67–. Denkschriften der Kaiserlichen Akademie, Christian/Mathematisch-Naturwissenschaftliche Classe. Mathematik, Wissenschaft. Allgemeine Transformation der bestimmten Doppel-Integrale. 155 dann b als positiv, so wird man nach einigen sich leicht anbietenden Reductionen sterben folgende Gleichung erhalten: Ich dx ff (ax'" von") dy=/tÃ¤7 H) - ir-r (-+-) m n i ttpÂ " ", "âf "4 // "âaf n â * w4 - âL-j.zm+n * f{z) dz I{âtf lt w*> dtA-/zm +7'lÃr-z) dzJ (lât) m'Â"' - + "'* j Macht man sterben noch speciellere Annahme, dass Â £ = oo, jy = oo sei, so wird der Mensch haben: O * CO fdx ff (a

RFR78GHX–Satz von Buchstaben logo Vorlage. Minimale schreiben Logo template Design

RF2N7P3PB–Modernes Design mit sechseckigem D-Logo. Logo-Vektor des DD D-Buchstabens für Technologie.

RF2CAJFTN–Alphabet Logo für Visitenkarte, Präsentation, Flyer, Dokument, Broschüre, Website, mobile. Kann für Marketing, Werbung, Promotion für onlin verwendet werden

RF2PPJ5WP–Einfaches Design mit quadratischem D-Logo. Abstrakter Logovektor für DD D-Buchstaben.

Eine elementare Abhandlung über Differentialgleichungen und deren Anwendungen. 2. die Tangente nicht zu Ox parallel könnte sein, so kann er sie nicht schneiden, butbecomes asymptotische. Die anderen Eigenschaften sind ähnlicher Natur. Beispiele für die Lösung. Skizze der Merkmale ofdy^ Dx (1) (2) y(l-x). = x2y. (3) dy dx-f = y + x2 dx 10. Singulären punkten. In allen Beispielen, wie die in der lastarticle, erhalten wir ein Merkmal, und nur eine, durch jeden Punkt Saj Ausschneiden/der Ebene. Durch die Verfolgung der beiden Kurven t | = 0 und ^- | = 0 Wir caneasily Skizze des Systems. Wenn jedoch f (x, y) wird unbestimmt fo Stockfoto

RM2ANA5KR–Eine elementare Abhandlung über Differentialgleichungen und deren Anwendungen. 2. die Tangente nicht zu Ox parallel könnte sein, so kann er sie nicht schneiden, butbecomes asymptotische. Die anderen Eigenschaften sind ähnlicher Natur. Beispiele für die Lösung. Skizze der Merkmale ofdy^ Dx (1) (2) y(l-x). = x2y. (3) dy dx-f = y + x2 dx 10. Singulären punkten. In allen Beispielen, wie die in der lastarticle, erhalten wir ein Merkmal, und nur eine, durch jeden Punkt Saj Ausschneiden/der Ebene. Durch die Verfolgung der beiden Kurven t | = 0 und ^- | = 0 Wir caneasily Skizze des Systems. Wenn jedoch f (x, y) wird unbestimmt fo

Frühe geophysikalische Papiere der Frühen geophysikalische Papiere der Gesellschaft der Exploration Geophysicists earlygeophysical 00 soci Jahr: 1947 i 58 Maurice Ewing und A. S. CRARY, wo v ist die Geschwindigkeit, mit der Tiefe y, erreicht ist. Eq. (2) Erträge dy/dx = ± (b2 Esc 2 0 O-v2) ll 2/v, (6), die mit (5) kombiniert werden, um die Relation zu geben: * = + (i/27 Ra) f v [(v2-b2)/(b 2 Esc 2 60-v2)] l'2 dv J b = (b2 Babybett 2 / 4 Ta) [a-sin a cos a], (7), wo die Sünde ein = ± tan 6 o (v2/b2-Iy 2. Das positive Vorzeichen sollte berücksichtigt werden, wenn die Welle seine maximale Tiefe nicht erreicht hat. 0,012 0,006 5 0.0O WÜRDE 4. 10 ft Vertikaler Abstand £ 0 40 Stockfoto

RMT0TXRN–Frühe geophysikalische Papiere der Frühen geophysikalische Papiere der Gesellschaft der Exploration Geophysicists earlygeophysical 00 soci Jahr: 1947 i 58 Maurice Ewing und A. S. CRARY, wo v ist die Geschwindigkeit, mit der Tiefe y, erreicht ist. Eq. (2) Erträge dy/dx = ± (b2 Esc 2 0 O-v2) ll 2/v, (6), die mit (5) kombiniert werden, um die Relation zu geben: * = + (i/27 Ra) f v [(v2-b2)/(b 2 Esc 2 60-v2)] l'2 dv J b = (b2 Babybett 2 / 4 Ta) [a-sin a cos a], (7), wo die Sünde ein = ± tan 6 o (v2/b2-Iy 2. Das positive Vorzeichen sollte berücksichtigt werden, wenn die Welle seine maximale Tiefe nicht erreicht hat. 0,012 0,006 5 0.0O WÜRDE 4. 10 ft Vertikaler Abstand £ 0 40

. Wörterbuch des sciences mathÃ©matiques pures et appliquÃ©es. fa' x 'x fx 'dx x x x x x x - 7 T^'fa^x dx Fx^ dx jX' = 'x = | LR quand x = LR. 9.. Trouver le centre de gravitÃ© De La Courbe para-bolique ALV. Ici, Puisqu'il s'agit d'une simple Ligne, l'Ã©lÃ©ment ds devient' ds=/dx - Dy ^^; â â â'Mais l'Ã©quation j>'' = ax nous Donne en diffÃ©rentiant dy = i^ai. xâidx ou Dj' =:^ ax 'x'. Nous avons donc. V 'D^+ dP=dxy/[i+^], et par consÃ©quent D:/aVv/[r + fJ/^ â/AV [+^> X Stockfoto

RMMEM460–. Wörterbuch des sciences mathÃ©matiques pures et appliquÃ©es. fa' x 'x fx 'dx x x x x x x - 7 T^'fa^x dx Fx^ dx jX' = 'x = | LR quand x = LR. 9.. Trouver le centre de gravitÃ© De La Courbe para-bolique ALV. Ici, Puisqu'il s'agit d'une simple Ligne, l'Ã©lÃ©ment ds devient' ds=/dx - Dy ^^; â â â'Mais l'Ã©quation j>'' = ax nous Donne en diffÃ©rentiant dy = i^ai. xâidx ou Dj' =:^ ax 'x'. Nous avons donc. V 'D^+ dP=dxy/[i+^], et par consÃ©quent D:/aVv/[r + fJ/^ â/AV [+^> X

RFR78G6X–Satz von Buchstaben logo Vorlage. Minimale schreiben Logo template Design

RF2N7HRCN–Einfaches Design mit quadratischem D-Logo. Abstrakter Logovektor für DD D-Buchstaben.

RF2PPJ0PJ–Minimalistisches Design-Set mit Buchstabe D Logo für Zuhause. Logo-Vektor mit DD D-Buchstaben des Hauses

Analyselemente, die auf die Mechanik von Maschinen und Maschinen angewendet werden. ^^^ Mx C hat nun die Fläche eines solchen Oberflächenelements ^ -J. J/Y=(y-f i dy) dx = ydx, g^=(5^ + ^^"^ der Bereich der gesamten Fläche F kann durch Integration des differentiellen ydx gefunden werden, wodurch F =f ydx gesetzt wird.Beispiel: Für eine Parabel mit dem Parameter p haben wir y^ =px, und damit die Oberfläche derselben: / 3 Vp^dx = Vpj xdx = --3--- = I ^ V px^ F xy. Die parabolische Oberfläche ab G ist also zwei Drittel der rec-tano-le AGB1), die sie umschließt. ARTIKEL 29.] ELEMENTE DER ANALYSE. 43 Diese Formel ist auch anwendbar Stockfoto

RM2AWF4XA–Analyselemente, die auf die Mechanik von Maschinen und Maschinen angewendet werden. ^^^ Mx C hat nun die Fläche eines solchen Oberflächenelements ^ -J. J/Y=(y-f i dy) dx = ydx, g^=(5^ + ^^"^ der Bereich der gesamten Fläche F kann durch Integration des differentiellen ydx gefunden werden, wodurch F =f ydx gesetzt wird.Beispiel: Für eine Parabel mit dem Parameter p haben wir y^ =px, und damit die Oberfläche derselben: / 3 Vp^dx = Vpj xdx = --3--- = I ^ V px^ F xy. Die parabolische Oberfläche ab G ist also zwei Drittel der rec-tano-le AGB1), die sie umschließt. ARTIKEL 29.] ELEMENTE DER ANALYSE. 43 Diese Formel ist auch anwendbar

. Economie forestiÃ¨re. Abb. 124. dx PT - PT. Â°^ PT^^ Ã ¯ ich Si nous prenons dx = 1, c'est-À-dire À © gal à l'Unità © de temps, Dy1 Nous avons donc â = 1^7; ? C'est-À-dire que le taux de formation y Pi^de la valeur à l'Ã¢ge OP, qui est, est prÃ©cisÃ © ment Ã © gal à l'in-Vers de la sous-Tangente au point M dont l'abscisse est OP. ConsidÃ©Rons d'autre Part une Somme d'Argent, de valeur Ã © Gale à Celle du Fonds, s'accroissant À un taux quelconque<, suivant la loi des intÃ©rÃªts composÃ©s. Sa valeur, au bout d'un temps x Stockfoto

RMMAA8CG–. Economie forestiÃ¨re. Abb. 124. dx PT - PT. Â°^ PT^^ Ã ¯ ich Si nous prenons dx = 1, c'est-À-dire À © gal à l'Unità © de temps, Dy1 Nous avons donc â = 1^7; ? C'est-À-dire que le taux de formation y Pi^de la valeur à l'Ã¢ge OP, qui est, est prÃ©cisÃ © ment Ã © gal à l'in-Vers de la sous-Tangente au point M dont l'abscisse est OP. ConsidÃ©Rons d'autre Part une Somme d'Argent, de valeur Ã © Gale à Celle du Fonds, s'accroissant À un taux quelconque<, suivant la loi des intÃ©rÃªts composÃ©s. Sa valeur, au bout d'un temps x

RF2N79BTN–Minimalistisches Design-Set mit Buchstabe D Logo für Zuhause. Logo-Vektor mit DD D-Buchstaben des Hauses

RF2PPJ09J–Modernes Design mit sechseckigem D-Logo. Logo-Vektor des DD D-Buchstabens für Technologie.

RM2ANF34C–Mechanik der engineeringComprising Statik und Dynamik von Festkörpern: und die Mechanik der Werkstoffe von Konstruktionen oder Festigkeit und Elastizität der Träger, Säulen, Bögen, Wellen, etc. 4 Wx+] U0+l %*. . (1) dx 2 2 v und.-. EI^=-y 2 W^+ Mox+^+[C=0]. (2) w = wl. Abb. 282. 330 MECHANIK VON ENGINEERING. Die Tangente an 0 als horizontale wir für x = 0, j = 0,.-. (7 = 0. Aber da die Tangente bei C ist auch hori-zontal, können wir für x-l, dy + dx = 0 und erhalten 0 = - % WP+m+j4 wP; woher M0=LJVl (3) Als Zeitpunkt des Stress-conple in der Nähe der Wand bei 0 und bei C, Abb. 283 Die Gleichsetzung von

$Die amerikanische Fachzeitschrift für Wissenschaft und Kunst. - F) usw. = F{xy), (A);^i4 i. t-^%^^ Amerikanische Zikade oder Heuschrecken. 49 Abschied t/^+ Aa: y-i-Bx^{-Cij--DX-{-E=0 in seiner einfachen factorsand haben wir {y + Ax + b){y-{- & x + d) = y+Axy+Bx ^----- Cy + Dx+E, (B) Vergleich der Faktoren von (B) und zwei von (A), zum Beispiel den Ersten und Zweiten, und wir haben eine - a, b = b, &=^c und d=d, und (B), wird ein Faktor von (A) Unabhängig von x und y, denn es sind butfour unabhängigen Koeffizienten in (B); die Koeffizienten in (B) beingknown in Funktionen der F{xy), wir haben sie fv-dx dy ^-^". Art.-V.-JVoiices und Beobachtungen Stockfoto$

RM2AKFR9C–Die amerikanische Fachzeitschrift für Wissenschaft und Kunst. - F) usw. = F{xy), (A);^i4 i. t-^%^^ Amerikanische Zikade oder Heuschrecken. 49 Abschied t/^+ Aa: y-i-Bx^{-Cij--DX-{-E=0 in seiner einfachen factorsand haben wir {y + Ax + b){y-{- & x + d) = y+Axy+Bx ^----- Cy + Dx+E, (B) Vergleich der Faktoren von (B) und zwei von (A), zum Beispiel den Ersten und Zweiten, und wir haben eine - a, b = b, &=^c und d=d, und (B), wird ein Faktor von (A) Unabhängig von x und y, denn es sind butfour unabhängigen Koeffizienten in (B); die Koeffizienten in (B) beingknown in Funktionen der F{xy), wir haben sie fv-dx dy ^-^". Art.-V.-JVoiices und Beobachtungen

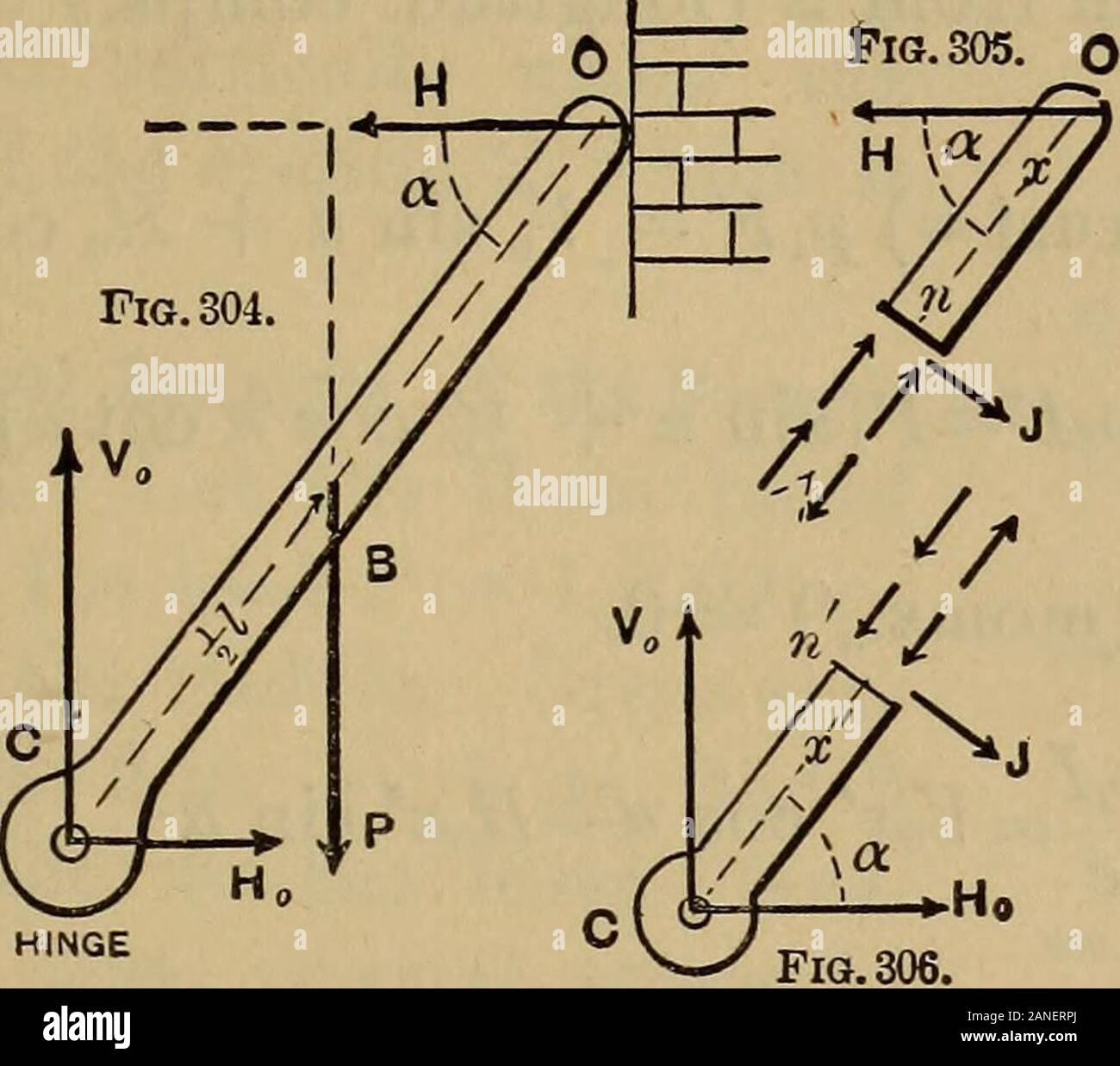$Mechanik der engineeringComprising Statik und Dynamik von Festkörpern: und die Mechanik der Werkstoffe von Konstruktionen oder Festigkeit und Elastizität der Träger, Säulen, Bögen, Wellen, etc. zu P Sünde", und P für Pcos ein. p-i Qx Qx konstante Faktoren, die wir jetzt y=- ^ schreiben, x-me n" • • die Gleichung erforderlich. (10) Zur Bestimmung der Konstanten m und (m-C+2q2; n=C-*-2 CQ4) wir erste dy + dx finden, d. h. dv v 2 $ x-Qx durch Differenzierung (10), ^r 2 + ymen + fl^n.... (11) z = 0fory = 0 0 0.. (10) gibt. . 0 - 0 - {- Männer - Dke = 0 d. h. m-n=0..m=n. (12) Auch für x=l dv p2 & - von -^- = 0.-. (11) liefert 0 = f q^n + nen • (1. Stockfoto$

RM2ANERPJ–Mechanik der engineeringComprising Statik und Dynamik von Festkörpern: und die Mechanik der Werkstoffe von Konstruktionen oder Festigkeit und Elastizität der Träger, Säulen, Bögen, Wellen, etc. zu P Sünde", und P für Pcos ein. p-i Qx Qx konstante Faktoren, die wir jetzt y=- ^ schreiben, x-me n" • • die Gleichung erforderlich. (10) Zur Bestimmung der Konstanten m und (m-C+2q2; n=C-*-2 CQ4) wir erste dy + dx finden, d. h. dv v 2 $ x-Qx durch Differenzierung (10), ^r 2 + ymen + fl^n.... (11) z = 0fory = 0 0 0.. (10) gibt. . 0 - 0 - {- Männer - Dke = 0 d. h. m-n=0..m=n. (12) Auch für x=l dv p2 & - von -^- = 0.-. (11) liefert 0 = f q^n + nen • (1.

Forhandlinger i Videnskabs-selskabet i Christiania . U{xyy)en tilvaext d TJ bestemmt ved ligningen: DTJ DTJ du = -- d x + x dy 4--- , dy "dx dy J n dy J der stiller sig nu det spørgsmaal, om det er mulig at finden saadan med L fast forbunden pilgroup, at summens afpilenes arbeider ved enhver uendelig liden bevagelse af L altid 1vil blive tilvaexten af det til L hørende utryk - TJ. Taenker VI os en pil med begyndelsespunkt i punktet xyog hvis Projektioner paa Xaxen og Faxen henholdsvis er lig 1 SZ7 1 du - os - -n dx n dy saa vil denne pil, som man strax ser, sammen med et medL fast forb Stockfoto

RM2AX93XP–Forhandlinger i Videnskabs-selskabet i Christiania . U{xyy)en tilvaext d TJ bestemmt ved ligningen: DTJ DTJ du = -- d x + x dy 4--- , dy "dx dy J n dy J der stiller sig nu det spørgsmaal, om det er mulig at finden saadan med L fast forbunden pilgroup, at summens afpilenes arbeider ved enhver uendelig liden bevagelse af L altid 1vil blive tilvaexten af det til L hørende utryk - TJ. Taenker VI os en pil med begyndelsespunkt i punktet xyog hvis Projektioner paa Xaxen og Faxen henholdsvis er lig 1 SZ7 1 du - os - -n dx n dy saa vil denne pil, som man strax ser, sammen med et medL fast forb

Forhandlinger i Videnskabs-selskabet i Christiania . V = + dy dx (21) ni = 3. MED andre betegnelser har VI da en flade i rammet: X = F (u, V)y = F2 (u, V)z = F% (u, V) 16 CARL STØRMER. [Nein 2. OG vor formel V= + Hf W OE, y, dx du dy dzdu dx DV dy ^ DV dzdv du dv (22) 1. UO -f u V0 4- V ±T 9J MO ^0 giver volumenet afen kegle med spidsi origo og til grund-flade et afgraensettykke S af fladensvarende til omraadeta i u, V Planet. Hvisspecifelt 8 er be-graenset af et par^-kurver og et parf-kurver, svarende re-spektive til u = u0, u u u u0 --u og V = V0, V = V0--vfaaes: A du dv (23) hvor A nar samme b Stockfoto

RM2AX9X4M–Forhandlinger i Videnskabs-selskabet i Christiania . V = + dy dx (21) ni = 3. MED andre betegnelser har VI da en flade i rammet: X = F (u, V)y = F2 (u, V)z = F% (u, V) 16 CARL STØRMER. [Nein 2. OG vor formel V= + Hf W OE, y, dx du dy dzdu dx DV dy ^ DV dzdv du dv (22) 1. UO -f u V0 4- V ±T 9J MO ^0 giver volumenet afen kegle med spidsi origo og til grund-flade et afgraensettykke S af fladensvarende til omraadeta i u, V Planet. Hvisspecifelt 8 er be-graenset af et par^-kurver og et parf-kurver, svarende re-spektive til u = u0, u u u u0 --u og V = V0, V = V0--vfaaes: A du dv (23) hvor A nar samme b

. Ein elementarer Kurs der Infinitesimalrechnung. G differenzierbarsind jedoch sehr selten vorkommen in der Mathematik, und wird nicht mit in diesem Buch. Es gibt verschiedene andere Notationen für die abgeleitete Funktion, anstelle von dy/dx. Die abgeleitete Funktion wird oft durch Anbringen eines Akzentzeichens an das Symbol, das die ursprüngliche Funktion bezeichnet, angezeigt. Wenn also y = t>i^) (3), kann die abgeleitete Funktion durch y oder durch ^ (*•) bezeichnet werden. Seit Sy^^(x+S^-^XJ OX bx haben wir, schreiben h für 8x, J./ T 6 (x + h) - (b (a) (/) («) = hmft^o ^^^^^ ^-^^^ (4). Die Operation der Ermittlung des Differentialkoeffizienten von agi Stockfoto

RM2CDC1B4–. Ein elementarer Kurs der Infinitesimalrechnung. G differenzierbarsind jedoch sehr selten vorkommen in der Mathematik, und wird nicht mit in diesem Buch. Es gibt verschiedene andere Notationen für die abgeleitete Funktion, anstelle von dy/dx. Die abgeleitete Funktion wird oft durch Anbringen eines Akzentzeichens an das Symbol, das die ursprüngliche Funktion bezeichnet, angezeigt. Wenn also y = t>i^) (3), kann die abgeleitete Funktion durch y oder durch ^ (*•) bezeichnet werden. Seit Sy^^(x+S^-^XJ OX bx haben wir, schreiben h für 8x, J./ T 6 (x + h) - (b (a) (/) («) = hmft^o ^^^^^ ^-^^^ (4). Die Operation der Ermittlung des Differentialkoeffizienten von agi

. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung. Wird positiv oder negativ aeeerding a^^ theangle pox = 0 ist größer oder kleiner als die aiuie JLo.v. Diese 432 INTEGRALRECHNUNG. Ergebnisse können für mehrere Zwecke verwendet werden^ die wichtigsten davon sind, - Erstens, um die Länge eines Teils einer Kurve zu finden, die Gleichung der Kurve gegeben wird. In diesem Fall können aus der Gleichung der Kurve und der Gleichung dy dx – COT.^, X und ?/ und damit ^:) = ic cos. d -- y sin. d, die Zwischenstufen von d bestimmt werden; und durch Integration kann s aus der Gleichung s = - gefunden werden Stockfoto

RM2CHB9Y4–. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung. Wird positiv oder negativ aeeerding a^^ theangle pox = 0 ist größer oder kleiner als die aiuie JLo.v. Diese 432 INTEGRALRECHNUNG. Ergebnisse können für mehrere Zwecke verwendet werden^ die wichtigsten davon sind, - Erstens, um die Länge eines Teils einer Kurve zu finden, die Gleichung der Kurve gegeben wird. In diesem Fall können aus der Gleichung der Kurve und der Gleichung dy dx – COT.^, X und ?/ und damit ^:) = ic cos. d -- y sin. d, die Zwischenstufen von d bestimmt werden; und durch Integration kann s aus der Gleichung s = - gefunden werden

. Eine Abhandlung über die mathematische Theorie der Elastizität. ds dxdy. Daraus folgt, dass die potentielle Energie pro Längeneinheit ^CV^ ist.217. Methode der Lösung des Torsionsproblems. Da <^ eine Ebene harmonische Funktion ist, gibt es eine konjugierte Funktion i/Rwas so ist, dass (^ + ti/r ist eine Funktion der komplexen Variablen x + L-y; Und wenn i/r gefunden werden kann, kann <^ mit Hilfe der Gleichungen 90 d^ dcf) dlrdy dy DX dx niedergeschrieben werden. Abb. 21. 9^it- 9^-vlrDie Funktion r erfüllt die Gleichung -^ + -^ = 0, an allen Punkten innerhalb der Begrenzungskurve des Querschnitts, und eine bestimmte Bedingung a Stockfoto

RM2CDFCFW–. Eine Abhandlung über die mathematische Theorie der Elastizität. ds dxdy. Daraus folgt, dass die potentielle Energie pro Längeneinheit ^CV^ ist.217. Methode der Lösung des Torsionsproblems. Da <^ eine Ebene harmonische Funktion ist, gibt es eine konjugierte Funktion i/Rwas so ist, dass (^ + ti/r ist eine Funktion der komplexen Variablen x + L-y; Und wenn i/r gefunden werden kann, kann <^ mit Hilfe der Gleichungen 90 d^ dcf) dlrdy dy DX dx niedergeschrieben werden. Abb. 21. 9^it- 9^-vlrDie Funktion r erfüllt die Gleichung -^ + -^ = 0, an allen Punkten innerhalb der Begrenzungskurve des Querschnitts, und eine bestimmte Bedingung a

. Angewandte Kalkül; Prinzipien und Anwendungen . s Pfad ist resultierende Geschwindigkeit, =S=V(f+(S)=^s >y a:-Komponente i^Vx = -7: = Geschwindigkeit parallel zur x-Achse, i/-Komponente mvy = -£ = Geschwindigkeit parallel zur ?/-Achse;, , dy dy / dx dy dx ^ , ^ , dy dy / ds dy ds . dx dx /ds dx ds dves scheint, dass -p, die Rate von y in Bezug auf x, ist das Verhältnis der Zeitrate von y zu der Zeitrate von x. Diese Ausdrücke für Geschwindigkeit und ihre Beziehungen umfassen den Fall, in dem die Bewegung gleichmäßig oder variabel entlang einer geraden Linie ist. 12. Rate, Geschwindigkeit und Beschleunigung. - Beschleunigung israte der Änderung der Geschwindigkeit oder vel Stockfoto

RM2CGH9Y6–. Angewandte Kalkül; Prinzipien und Anwendungen . s Pfad ist resultierende Geschwindigkeit, =S=V(f+(S)=^s >y a:-Komponente i^Vx = -7: = Geschwindigkeit parallel zur x-Achse, i/-Komponente mvy = -£ = Geschwindigkeit parallel zur ?/-Achse;, , dy dy / dx dy dx ^ , ^ , dy dy / ds dy ds . dx dx /ds dx ds dves scheint, dass -p, die Rate von y in Bezug auf x, ist das Verhältnis der Zeitrate von y zu der Zeitrate von x. Diese Ausdrücke für Geschwindigkeit und ihre Beziehungen umfassen den Fall, in dem die Bewegung gleichmäßig oder variabel entlang einer geraden Linie ist. 12. Rate, Geschwindigkeit und Beschleunigung. - Beschleunigung israte der Änderung der Geschwindigkeit oder vel

. Angewandte Kalkül; Grundsätze und Anwendungen . ADEN wird ermittelt, wie in (2) angegeben.Daher ist A= f fdx dy (4) im Allgemeinen die Formel für Fläche durch Doppelintegration, die Grenzwerte werden so festgelegt, dass der erforderliche Bereich einbezogen wird. Die Ordnung der Integration ist indifferent, sofern die Grenzen der Reihenfolge angepasst werden. Folge. – dxy^A = dx dy und Dyx^A = dy dx. Beispiel 1. - Finden Sie den Bereich durch die Parabolasy begrenzt^ = 2px und x^ = 2 py. Die Parabeln schneiden sich an den Punkten (0, 0) und (2 p, 2 p). I dxdy = ^ p^, nach Formel (2). 0 J x2 Jo J «2 2p2/ dydx = ^ p^, nach Formel (3). 2p Beispiel 2. - Finden Sie die ar Stockfoto

RM2CGGHEG–. Angewandte Kalkül; Grundsätze und Anwendungen . ADEN wird ermittelt, wie in (2) angegeben.Daher ist A= f fdx dy (4) im Allgemeinen die Formel für Fläche durch Doppelintegration, die Grenzwerte werden so festgelegt, dass der erforderliche Bereich einbezogen wird. Die Ordnung der Integration ist indifferent, sofern die Grenzen der Reihenfolge angepasst werden. Folge. – dxy^A = dx dy und Dyx^A = dy dx. Beispiel 1. - Finden Sie den Bereich durch die Parabolasy begrenzt^ = 2px und x^ = 2 py. Die Parabeln schneiden sich an den Punkten (0, 0) und (2 p, 2 p). I dxdy = ^ p^, nach Formel (2). 0 J x2 Jo J «2 2p2/ dydx = ^ p^, nach Formel (3). 2p Beispiel 2. - Finden Sie die ar

. Differential-und Integralrechnung. Erential Calculus 125. Um die sukzessiven Gesamtdifferentiale einer Funktion von zwei unabhängigen Variablen zu finden. Let U = f(x,y); then, (§121), du du du = – doc -+- – dy.dx dy ^•rr • • . . 8U - Sit differenzierend, daran erinnern, dass - und - sind im Allgemeinen, Funktionen von x und y, und dass x und y, unabhängig, kann als gleichbedeutend angesehen werden, haben wir, V2 &U J 2 J. &U D2U .^ ., dx2 dxdy dydx df d2u d2u d2u ähnlich finden wir, d^U dsu d^U d^U d*U = &3 + 3 dx,dy + 3 ^dxdf + da usw. Durch die Beobachtung der Analogie zwischen den Exponenten von du, d2u, d*U, . Stockfoto

RM2CEPFDX–. Differential-und Integralrechnung. Erential Calculus 125. Um die sukzessiven Gesamtdifferentiale einer Funktion von zwei unabhängigen Variablen zu finden. Let U = f(x,y); then, (§121), du du du = – doc -+- – dy.dx dy ^•rr • • . . 8U - Sit differenzierend, daran erinnern, dass - und - sind im Allgemeinen, Funktionen von x und y, und dass x und y, unabhängig, kann als gleichbedeutend angesehen werden, haben wir, V2 &U J 2 J. &U D2U .^ ., dx2 dxdy dydx df d2u d2u d2u ähnlich finden wir, d^U dsu d^U d^U d*U = &3 + 3 dx,dy + 3 ^dxdf + da usw. Durch die Beobachtung der Analogie zwischen den Exponenten von du, d2u, d*U, .

$. Angewandte Kalkül; Prinzipien und Anwendungen . zum Zentrum der Krümmung. Dann ist PC R und ist rechtwinklig die Tangente PT. Daher Z BCP = Z XTP = 0, OA = OM - BP, AC = MP-- BC; A = x – RSM(i), ^ = y -- RCOS(f); (1) T^dy ^ , -^dx das ist, oder (2) EIGENSCHAFTEN DER EVOLVENTE UND EVOLUTE 143 Substitution in (2). Die Werte von R und ds, ergibt A = X dx 1 + ^ = y + 1^1 dx/ d^dx (3) 95. Evoluten und Evoluten. - jeder Punkt einer Kurve, wie in, hat ein entsprechendes Zentrum der Krümmung. Wenn sich der Punkt (x, y) entlang der Kurve bewegt, wird der Punkt {a, ^) durch die obige Gleichung (3) eine weitere Kurve als EV nachzeichnen. T Stockfoto$

RM2CGH3J9–. Angewandte Kalkül; Prinzipien und Anwendungen . zum Zentrum der Krümmung. Dann ist PC R und ist rechtwinklig die Tangente PT. Daher Z BCP = Z XTP = 0, OA = OM - BP, AC = MP-- BC; A = x – RSM(i), ^ = y -- RCOS(f); (1) T^dy ^ , -^dx das ist, oder (2) EIGENSCHAFTEN DER EVOLVENTE UND EVOLUTE 143 Substitution in (2). Die Werte von R und ds, ergibt A = X dx 1 + ^ = y + 1^1 dx/ d^dx (3) 95. Evoluten und Evoluten. - jeder Punkt einer Kurve, wie in, hat ein entsprechendes Zentrum der Krümmung. Wenn sich der Punkt (x, y) entlang der Kurve bewegt, wird der Punkt {a, ^) durch die obige Gleichung (3) eine weitere Kurve als EV nachzeichnen. T

. Differential-und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. Chorder drei aufeinanderfolgenden Integrationen durchgeführt werden, Sorgfalt beigtaken in jedem Fall zu angemessenen Grenzen zu beschäftigen. Beispiel. Finden wir den Wert des Dreifachintegrals J J j xdzdy dx, V, wobei V der Raum ist, der in einem Oktant der Kugel enthalten ist x2 + y1 + z1 = r2.erste Lösung. Wir schneiden V in Schichten von Ebenen parallel zu der yz-psme.Aufruf des Dreifach-Integral I, haben wir x=r y= V r2 – x2 z= V?i – xi – y2 I = j J j x dz dy dx, x=0 y=0 z=0 die Grenzen der Integration wird wie folgt bestimmt:im ersten int Stockfoto

RM2CEJ72N–. Differential-und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. Chorder drei aufeinanderfolgenden Integrationen durchgeführt werden, Sorgfalt beigtaken in jedem Fall zu angemessenen Grenzen zu beschäftigen. Beispiel. Finden wir den Wert des Dreifachintegrals J J j xdzdy dx, V, wobei V der Raum ist, der in einem Oktant der Kugel enthalten ist x2 + y1 + z1 = r2.erste Lösung. Wir schneiden V in Schichten von Ebenen parallel zu der yz-psme.Aufruf des Dreifach-Integral I, haben wir x=r y= V r2 – x2 z= V?i – xi – y2 I = j J j x dz dy dx, x=0 y=0 z=0 die Grenzen der Integration wird wie folgt bestimmt:im ersten int

. Differential-und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. i{x, y) und z = f2(x, y)Be die Gleichungen von 1 Dollar bzw. 2 Dollar, können wir schreiben V = i ffi(x, y) dydx - J i f2(x, y) dy dx = J i (ft -/2) dy dx, R R R R, die nachgewiesen werden sollte. Beispiel. Finden wir durch Doppelintegration das Volumen der Kugel (x - a)2 +(y- b)2 + (z - c)2 = r2.in diesem Fall ist R der Kreis (x - a)2 + (y - b)2 = r2, und die Grenzen der Integration für y sind y = b - Vr2 - {x – a)2 = y{x) und y = b + Vr2 – (x – a)2 = d(x). §215 MULTIPLE INTEGRALE 327 Darüber hinaus die Gleichungen von Si und S2 Stockfoto

RM2CEJ8BR–. Differential-und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. i{x, y) und z = f2(x, y)Be die Gleichungen von 1 Dollar bzw. 2 Dollar, können wir schreiben V = i ffi(x, y) dydx - J i f2(x, y) dy dx = J i (ft -/2) dy dx, R R R R, die nachgewiesen werden sollte. Beispiel. Finden wir durch Doppelintegration das Volumen der Kugel (x - a)2 +(y- b)2 + (z - c)2 = r2.in diesem Fall ist R der Kreis (x - a)2 + (y - b)2 = r2, und die Grenzen der Integration für y sind y = b - Vr2 - {x – a)2 = y{x) und y = b + Vr2 – (x – a)2 = d(x). §215 MULTIPLE INTEGRALE 327 Darüber hinaus die Gleichungen von Si und S2

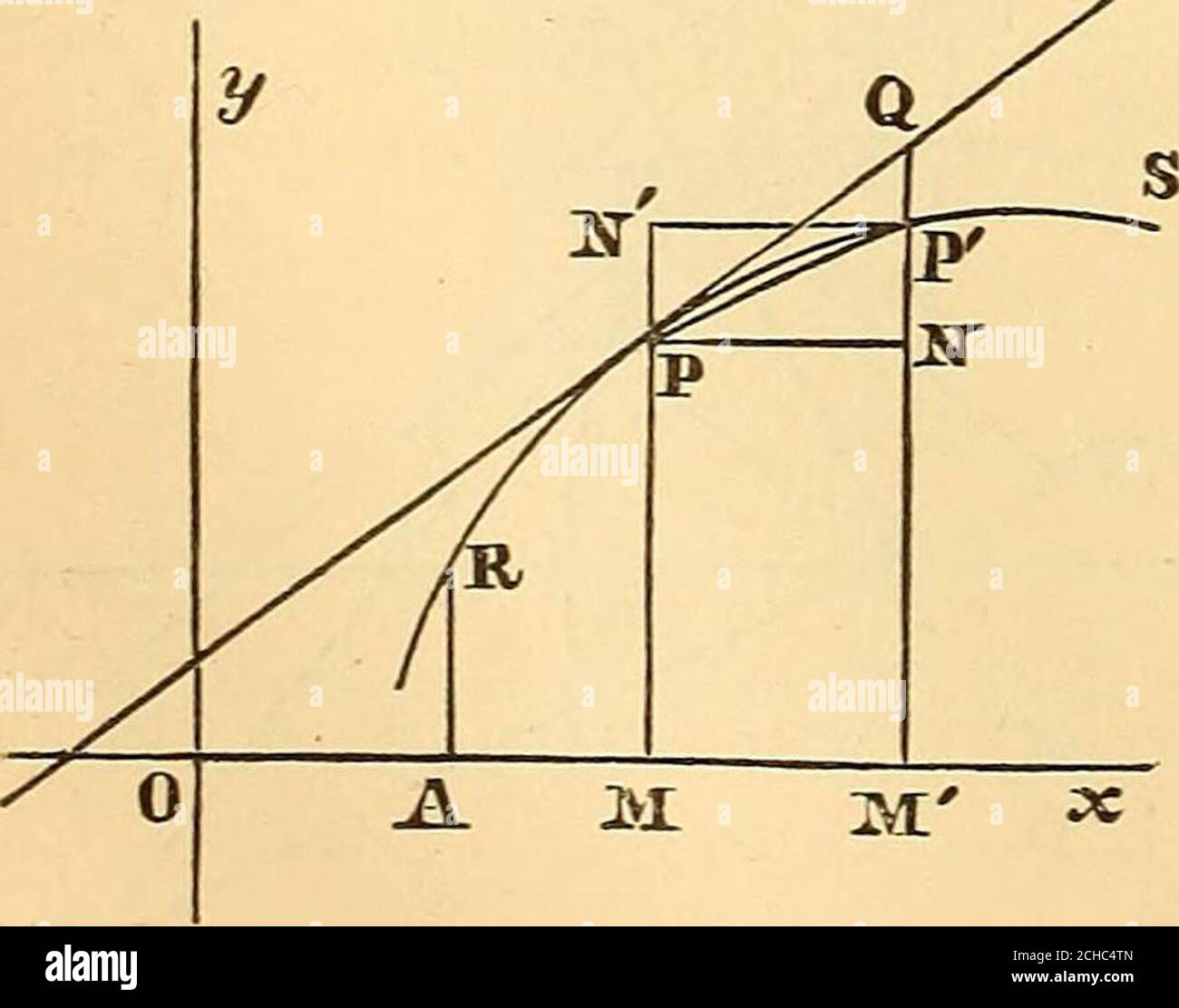. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung . re, und die Radien vectoresF3I^= r, FS^=^ r^ als Radien, beschreiben die Arcs MIY SK, begrenzt durch diese Radien vectores. Wir haben Sektor PJ/7 < A?^ SX; oder, da Sektor PJ/J =7^ r-A^ und Sektor P/S^ r^^^, --r-A^< ^U <-r^2^6; 1 < - < T ^ A^ ^ 2, aber an der Grenze wird r gleich r: Daher du 1 , du 1= -r^dd. Y die Gleichungen ic=rrcos./9, ?/ = rsin. (9, Geben - = Bräune. (9; woher,durch Unterscheiden in Bezug auf 6^ dy dx ^ddydo cos.-^(? r^ COS.!cos.-(? = 7-, ^(^xdy – ijdx) zzz-r^dd; ein Ausdruck im Sinne von rec Stockfoto

RM2CHC4TN–. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung . re, und die Radien vectoresF3I^= r, FS^=^ r^ als Radien, beschreiben die Arcs MIY SK, begrenzt durch diese Radien vectores. Wir haben Sektor PJ/7 < A?^ SX; oder, da Sektor PJ/J =7^ r-A^ und Sektor P/S^ r^^^, --r-A^< ^U <-r^2^6; 1 < - < T ^ A^ ^ 2, aber an der Grenze wird r gleich r: Daher du 1 , du 1= -r^dd. Y die Gleichungen ic=rrcos./9, ?/ = rsin. (9, Geben - = Bräune. (9; woher,durch Unterscheiden in Bezug auf 6^ dy dx ^ddydo cos.-^(? r^ COS.!cos.-(? = 7-, ^(^xdy – ijdx) zzz-r^dd; ein Ausdruck im Sinne von rec

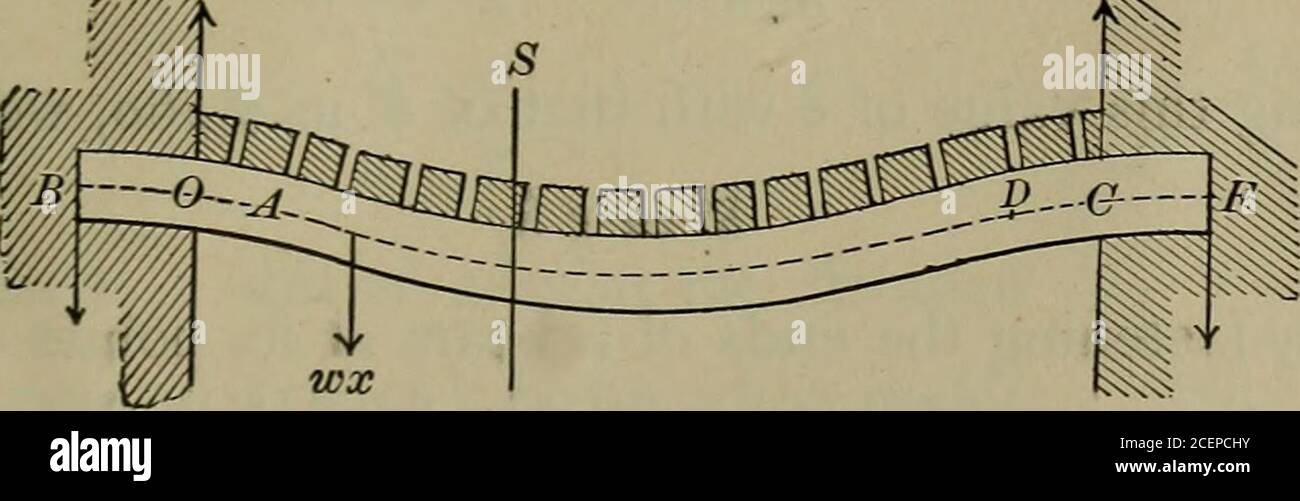$. Differential- und Integralrechnung. Abb. 72. In diesem Fall haben wir ? X wl w, . N J/ = #/# • ,3; = – (jt – /.*:). 22 2 V 7 Daher ^^ 7£/ = tML* -- U) Mechanische Anwendungen 391 daher dy dx 2 Ei (Ft)- / dyWhen x = - i -j- = o 2 tf# C = .1 7£/324^7 Daher 7i, wenn IX2 P 2 12 dx 2 Ei k w { x4 lxs px ?• y = – wy r1 2 -ZSY / 12 6 12 seit # = o, y = o; .-. C = o. / ., 5 wl< = 5 ET/3 384^/ 384^/ Wenn # = - , dann 2 Kor. Wenn wir den Wert von S von § 259 mit S dieses Artikels vergleichen, finden wir 8 = f8, d.h. die Durchbiegung, die durch eine am Zentner eines Strahls konzentrierte Last erzeugt wird, ist f von der, die vom erzeugt wird Stockfoto$

RM2CEPCHY–. Differential- und Integralrechnung. Abb. 72. In diesem Fall haben wir ? X wl w, . N J/ = #/# • ,3; = – (jt – /.*:). 22 2 V 7 Daher ^^ 7£/ = tML* -- U) Mechanische Anwendungen 391 daher dy dx 2 Ei (Ft)- / dyWhen x = - i -j- = o 2 tf# C = .1 7£/324^7 Daher 7i, wenn IX2 P 2 12 dx 2 Ei k w { x4 lxs px ?• y = – wy r1 2 -ZSY / 12 6 12 seit # = o, y = o; .-. C = o. / ., 5 wl< = 5 ET/3 384^/ 384^/ Wenn # = - , dann 2 Kor. Wenn wir den Wert von S von § 259 mit S dieses Artikels vergleichen, finden wir 8 = f8, d.h. die Durchbiegung, die durch eine am Zentner eines Strahls konzentrierte Last erzeugt wird, ist f von der, die vom erzeugt wird

$. Differential- und Integralrechnung. Daher DX Ei 4/ . V W /xz px Integration von agam, y = –^ ( - – )• seit # = o, y == o.; ,*, C = o. Wenn x = - haben wir 8 = 0 .2 4.8 £f 260. Form und Abbiegung eines an beiden Enden abgestützten Strahls undgleichmäßig belastet. Abb. 72. In diesem Fall haben wir ? X wl w, . N J/ = #/# • ,3; = – (jt – /.*:). 22 2 V 7 Daher ^^ 7£/ = tML* -- U) Mechanische Anwendungen 391 daher dy dx 2 Ei (Ft)- / dyWhen x = - i -j- = o 2 tf# C = .1 7£/324^7 Daher 7i, wenn IX2 P 2 12 dx 2 Ei k w { x4 lxs px ?• y = – wy r1 2 -ZSY / 12 6 12 seit # = o, y = o; .-. C = o. / ., 5 wl< = 5 Stockfoto$

RM2CEPCK1–. Differential- und Integralrechnung. Daher DX Ei 4/ . V W /xz px Integration von agam, y = –^ ( - – )• seit # = o, y == o.; ,*, C = o. Wenn x = - haben wir 8 = 0 .2 4.8 £f 260. Form und Abbiegung eines an beiden Enden abgestützten Strahls undgleichmäßig belastet. Abb. 72. In diesem Fall haben wir ? X wl w, . N J/ = #/# • ,3; = – (jt – /.*:). 22 2 V 7 Daher ^^ 7£/ = tML* -- U) Mechanische Anwendungen 391 daher dy dx 2 Ei (Ft)- / dyWhen x = - i -j- = o 2 tf# C = .1 7£/324^7 Daher 7i, wenn IX2 P 2 12 dx 2 Ei k w { x4 lxs px ?• y = – wy r1 2 -ZSY / 12 6 12 seit # = o, y = o; .-. C = o. / ., 5 wl< = 5

$. Differential-und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. §215 MULTIPLE INTEGRALE 327 Darüber hinaus sind die Gleichungen von Si und S2 z = c + Vr2 - (x - af - (y - 6)2 = fx{x, y), Und z = c - Vr2 - (x - a)2 - (y - b)2 = f2 (x, y).Daher x = a+r y=S(x) Vx=j f[c + ^r*-(x-ay-(y-by]dydx, a a+r x – a – r y=y(x) x=a+r y d(x- v2 und x{=a- x. r y=S(x) V=V1-V2 = ff(fl-f2)dydx = 2J f Vr2 - (x - A)2 -(y- 6)2 dy dx. R x = a – r y=y{x) Integrieren durch die Integraltabelle, haben wir y=8(x) f Vr2-(x-ay-(y-b)2dy ={(y -b)Vr2-(x-a y-{y-by y=y x) 2/=6+V/r Stockfoto$

RM2CEJ83N–. Differential-und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. §215 MULTIPLE INTEGRALE 327 Darüber hinaus sind die Gleichungen von Si und S2 z = c + Vr2 - (x - af - (y - 6)2 = fx{x, y), Und z = c - Vr2 - (x - a)2 - (y - b)2 = f2 (x, y).Daher x = a+r y=S(x) Vx=j f[c + ^r*-(x-ay-(y-by]dydx, a a+r x – a – r y=y(x) x=a+r y d(x- v2 und x{=a- x. r y=S(x) V=V1-V2 = ff(fl-f2)dydx = 2J f Vr2 - (x - A)2 -(y- 6)2 dy dx. R x = a – r y=y{x) Integrieren durch die Integraltabelle, haben wir y=8(x) f Vr2-(x-ay-(y-b)2dy ={(y -b)Vr2-(x-a y-{y-by y=y x) 2/=6+V/r

. Ein Kommentar auf die wissenschaftlichen Schriften von J. Willard Gibbs. Gibbs, Joniah Willard, 1839-1908; Wissenschaft; Thermodynamik. Angespannte elastischen Feststoffen 467 Raum durch die Oberfläche s' begrenzt, dann die drei folgenden Beziehungen sind wahre^, dx ' dy ' dz '=a' 4> Ds', ox I30 dy-, dx ' dy ' dz'=/l3' (I> Ds',^ dx ' dy ' dz'=/y' (}> Ds', dz I, wo die Lautstärke Integrationen werden in der gesamten re getroffen werden - (i'K'). Bitte beachten Sie, dass diese Bilder extrahiert werden aus der gescannten Seite Bilder, die digital haben für die Lesbarkeit verbessert - Färbung und Aussehen dieser Abbildungen können nicht Pro Stockfoto

RMREGNKA–. Ein Kommentar auf die wissenschaftlichen Schriften von J. Willard Gibbs. Gibbs, Joniah Willard, 1839-1908; Wissenschaft; Thermodynamik. Angespannte elastischen Feststoffen 467 Raum durch die Oberfläche s' begrenzt, dann die drei folgenden Beziehungen sind wahre^, dx ' dy ' dz '=a' 4> Ds', ox I30 dy-, dx ' dy ' dz'=/l3' (I> Ds',^ dx ' dy ' dz'=/y' (}> Ds', dz I, wo die Lautstärke Integrationen werden in der gesamten re getroffen werden - (i'K'). Bitte beachten Sie, dass diese Bilder extrahiert werden aus der gescannten Seite Bilder, die digital haben für die Lesbarkeit verbessert - Färbung und Aussehen dieser Abbildungen können nicht Pro

. Biophysik: Konzepte und Mechanismen. Biophysik. Die zehn Säulen 23 der Serie von ekx gekennzeichnet ist die einzige funktionale Beziehung in allen Medienseminar-matics, für die Ihre momentane Änderungsrate bei einem Wert von x genau proportional zu sich. Das heißt, es ist die einzige Funktion, für die beiden y eine ekx (1-4) und dy/d.v "ekx (oder "y) (1-5) wahr sind. Für Vollständigkeit, wenn die proportionalitätskonstante in Eq. (1-4) Intro ist - eingeführt, y=y^--- (1-4") und dy/dx = ky 0 ekx, (l-5') oder dy/dx = ky, erklärt die Bedeutung der ex in der Mathematik. Die Bedeutung In der Biophysik ist, dass eine tolle Stockfoto

RMRHK2WP–. Biophysik: Konzepte und Mechanismen. Biophysik. Die zehn Säulen 23 der Serie von ekx gekennzeichnet ist die einzige funktionale Beziehung in allen Medienseminar-matics, für die Ihre momentane Änderungsrate bei einem Wert von x genau proportional zu sich. Das heißt, es ist die einzige Funktion, für die beiden y eine ekx (1-4) und dy/d.v "ekx (oder "y) (1-5) wahr sind. Für Vollständigkeit, wenn die proportionalitätskonstante in Eq. (1-4) Intro ist - eingeführt, y=y^--- (1-4") und dy/dx = ky 0 ekx, (l-5') oder dy/dx = ky, erklärt die Bedeutung der ex in der Mathematik. Die Bedeutung In der Biophysik ist, dass eine tolle

. Abhandlungen der Königlich Bayerischen Akademie, Christian, mathematisch-physikalische Klasse. Wissenschaft. 24 51) Das Figuren 11 und 12 endlich beziehen sich auf die Optimierung dx = y* und dy dx y als einfachste Fälle unserer Optimierung sterben, für welche sterben Integrale algebraische Kurven sind. Abb. 11.. Ficr. 12.. Bitte beachten Sie, dass diese Bilder sind von der gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Aussehen dieser Abbildungen können nicht perfekt dem Original ähneln. extrahiert. Königlich Bayerische Akademie der Wi Stockfoto

RMRR7K7N–. Abhandlungen der Königlich Bayerischen Akademie, Christian, mathematisch-physikalische Klasse. Wissenschaft. 24 51) Das Figuren 11 und 12 endlich beziehen sich auf die Optimierung dx = y* und dy dx y als einfachste Fälle unserer Optimierung sterben, für welche sterben Integrale algebraische Kurven sind. Abb. 11.. Ficr. 12.. Bitte beachten Sie, dass diese Bilder sind von der gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Aussehen dieser Abbildungen können nicht perfekt dem Original ähneln. extrahiert. Königlich Bayerische Akademie der Wi

. Frühe geophysikalische Papiere der Gesellschaft der Exploration Geophysicists. Petroleum; Kundenakquise. Ich 58 Maurice Ewing und A. S. CRARY, wo v ist die Geschwindigkeit, mit der Tiefe y, erreicht ist. Eq. (2) Erträge dy/dx = ± (b2 Esc 2 0 O-v2) ll 2/v, (6), die mit (5) kombiniert werden, um die Relation zu geben: * = + (i/27 Ra) f v [(v2-b2)/(b 2 Esc 2 60-v2)] l'2 dv J b = (b2 Babybett 2 / 4 Ta) [a-sin a cos a], (7), wo die Sünde ein = ± tan 6 o (v2/b2-Iy 2. Das positive Vorzeichen sollte berücksichtigt werden, wenn die Welle seine maximale Tiefe nicht erreicht hat. 0,012" D 0,006 5 0.0O4.. 10 ft Vertikaler Abstand £ 0 40 60 ft. Horiiontal Entfernung Abb. 6.-Tr Stockfoto

RMRE9E6R–. Frühe geophysikalische Papiere der Gesellschaft der Exploration Geophysicists. Petroleum; Kundenakquise. Ich 58 Maurice Ewing und A. S. CRARY, wo v ist die Geschwindigkeit, mit der Tiefe y, erreicht ist. Eq. (2) Erträge dy/dx = ± (b2 Esc 2 0 O-v2) ll 2/v, (6), die mit (5) kombiniert werden, um die Relation zu geben: * = + (i/27 Ra) f v [(v2-b2)/(b 2 Esc 2 60-v2)] l'2 dv J b = (b2 Babybett 2 / 4 Ta) [a-sin a cos a], (7), wo die Sünde ein = ± tan 6 o (v2/b2-Iy 2. Das positive Vorzeichen sollte berücksichtigt werden, wenn die Welle seine maximale Tiefe nicht erreicht hat. 0,012" D 0,006 5 0.0O4.. 10 ft Vertikaler Abstand £ 0 40 60 ft. Horiiontal Entfernung Abb. 6.-Tr

$. Annalen der Philosophie. Ist^ G."] "Parameter für die Bestimmung bestimmter Kurven. 323I 6 a^x-Sax'' f6a", "X-S a x (X + x)-2a {X + x)" - + x (X + x) - j - + (x + a;) '-x.: (X + xf = 4 Xx.: (X-XF = 0.*. X=X8 X = 4 X * + (J/J) -^... (3^ Y) = 2 (2a X-X" -) h (2a X-X')^ IX (2 O-X) X dX dY dX2, a-X) (2) aX-X^^ die Gleichung einer zykloide, gleich und ähnlich der Ehemaligen, der seinen Ursprung in der Extremität der Base statt der Vertex, - eine bekannte Eigenschaft der Kurve. Auf die oben genannte Methode der Evolvente, können wir die folgenden Bemerkungen machen. 1. Die involut Stockfoto$

RMRMNDPB–. Annalen der Philosophie. Ist^ G."] "Parameter für die Bestimmung bestimmter Kurven. 323I 6 a^x-Sax'' f6a", "X-S a x (X + x)-2a {X + x)" - + x (X + x) - j - + (x + a;) '-x.: (X + xf = 4 Xx.: (X-XF = 0.*. X=X8 X = 4 X * + (J/J) -^... (3^ Y) = 2 (2a X-X" -) h (2a X-X')^ IX (2 O-X) X dX dY dX2, a-X) (2) aX-X^^ die Gleichung einer zykloide, gleich und ähnlich der Ehemaligen, der seinen Ursprung in der Extremität der Base statt der Vertex, - eine bekannte Eigenschaft der Kurve. Auf die oben genannte Methode der Evolvente, können wir die folgenden Bemerkungen machen. 1. Die involut

$. Acta Societatis Scientiarum Fennicae. Wissenschaft. Abb. 3.. (12) J< -^- dx + Ydy) = U - M CO dY dX ^ , dxay, dx dy) wird das Integral links Ringe herum ausgestreckt werden muss. Weil ferner die Bedingung dy dY dx überall innerhalb O erfüllt ist, so folgt aus (12) (13) ({Xdx - irYdy) = ^0. Diejenigen Teile dieses Integrale, welche von den (Zusammenfallenden) Rändern AB und CD herrühren, heben sich gegenseitig auf, weil X und Y in Nummern-oper Rändern gleich, Dx und Dy entgegengesetzt sind. Mann findet auch mit leicht verständlichen Bezeichnungen J (l) + J (2) = 0 Ja) = J (2). &Amp; oder (14) G^G^ Das in einer b Stockfoto$

RMRR3RDK–. Acta Societatis Scientiarum Fennicae. Wissenschaft. Abb. 3.. (12) J< -^- dx + Ydy) = U - M CO dY dX ^ , dxay, dx dy) wird das Integral links Ringe herum ausgestreckt werden muss. Weil ferner die Bedingung dy dY dx überall innerhalb O erfüllt ist, so folgt aus (12) (13) ({Xdx - irYdy) = ^0. Diejenigen Teile dieses Integrale, welche von den (Zusammenfallenden) Rändern AB und CD herrühren, heben sich gegenseitig auf, weil X und Y in Nummern-oper Rändern gleich, Dx und Dy entgegengesetzt sind. Mann findet auch mit leicht verständlichen Bezeichnungen J (l) + J (2) = 0 Ja) = J (2). &Amp; oder (14) G^G^ Das in einer b

. Acta Societatis Scientiarum Fennicae. Wissenschaft. Mechanische Arbeit in der Ebene. 1. Auf einen Punkt C mit den Coordinaten x, y m Bezug auf y^wetten dass X, Y und ihre ersten Ableitungen in der I I I I I I Ö'. reclitwinklige Axn wirke eine Kraft P mit den Componenten X und Y parallele denselben Axn. Es wird angenommen, dass X und Y nur von den Coordinaten x und?/, nicht aber von Human Ableitungen in Bezug auf die Zeit abhängen. Ferner werde zunächst vorausgesetzt, dX^d^^ öY dY dx ' dy^^ dx dy ganzen endhchen Ebene stetig seien. Die elementare Arbeit der Kraft P bei der Helvetica ihres Angriffspu Stockfoto

RMRR3RE2–. Acta Societatis Scientiarum Fennicae. Wissenschaft. Mechanische Arbeit in der Ebene. 1. Auf einen Punkt C mit den Coordinaten x, y m Bezug auf y^wetten dass X, Y und ihre ersten Ableitungen in der I I I I I I Ö'. reclitwinklige Axn wirke eine Kraft P mit den Componenten X und Y parallele denselben Axn. Es wird angenommen, dass X und Y nur von den Coordinaten x und?/, nicht aber von Human Ableitungen in Bezug auf die Zeit abhängen. Ferner werde zunächst vorausgesetzt, dX^d^^ öY dY dx ' dy^^ dx dy ganzen endhchen Ebene stetig seien. Die elementare Arbeit der Kraft P bei der Helvetica ihres Angriffspu

. Bulletin de la SociÃ©tÃ© impÃ©riale des naturalistes de Moscou. Wissenschaft; Biologie; Geologie; Natural History. J.^/^ Hebeln depuis la Oberfläche libre du liquide, jusqu'à Son in-tÃ©rieur, est une quantitÃ© constante, auf pourra Poser 2^b-i-n-i-(Ã d^= Ã, oÃ¹ Ð Einrichtung signe une quantitÃ© constante; l'Ã©quation prÃ© Cà©-dente prendra donc cette forme. C'est l'Ã©quation de la Oberfläche libre du Fluide. Soient Pj et p les deux Rayone principaux de quelnonque courbure dans un point de la Oberfläche libre, auf einem pj Pj dx dy dx Ð ¯. dy. Bitte beachten Sie, dass diese Bilder aus gescannten Seite Bilder extrahiert werden tha Stockfoto

RMRGPJH3–. Bulletin de la SociÃ©tÃ© impÃ©riale des naturalistes de Moscou. Wissenschaft; Biologie; Geologie; Natural History. J.^/^ Hebeln depuis la Oberfläche libre du liquide, jusqu'à Son in-tÃ©rieur, est une quantitÃ© constante, auf pourra Poser 2^b-i-n-i-(Ã d^= Ã, oÃ¹ Ð Einrichtung signe une quantitÃ© constante; l'Ã©quation prÃ© Cà©-dente prendra donc cette forme. C'est l'Ã©quation de la Oberfläche libre du Fluide. Soient Pj et p les deux Rayone principaux de quelnonque courbure dans un point de la Oberfläche libre, auf einem pj Pj dx dy dx Ð ¯. dy. Bitte beachten Sie, dass diese Bilder aus gescannten Seite Bilder extrahiert werden tha

. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. 28, Astronomie, GEODESIE MATHEMATIQUES ET MÃCANIQUE 1° Une übersetzung parallÃ¨le Ã OCHSEN; 2 "Une rotation Autour du Punkt R; 3 "Une Verstärkung proportionnelle des Abmessungen linÃ © Aires du Triangle, qui l'amÃ¨ne Ã sa nouvelle Pracht. 1° La übersetzung parallÃ¨le Ã OX est mesurÃ©e par la diffÃ©rentielle d x âyi.de l'abscisse du Punkt R, c'est-À-dire Auto dy dx â d (y Kinderbett y.) = Dx - dr Kinderbett a A-y. .' Dx = d) Babybett vgl.. --J-sm y. 52° La rotation Autour du Punkt R est donnÃ©e par la diffÃ©rentielle dx de l'Angle ein. Ces deux mouv Stockfoto

RMREDBMN–. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. 28, Astronomie, GEODESIE MATHEMATIQUES ET MÃCANIQUE 1° Une übersetzung parallÃ¨le Ã OCHSEN; 2 "Une rotation Autour du Punkt R; 3 "Une Verstärkung proportionnelle des Abmessungen linÃ © Aires du Triangle, qui l'amÃ¨ne Ã sa nouvelle Pracht. 1° La übersetzung parallÃ¨le Ã OX est mesurÃ©e par la diffÃ©rentielle d x âyi.de l'abscisse du Punkt R, c'est-À-dire Auto dy dx â d (y Kinderbett y.) = Dx - dr Kinderbett a A-y. .' Dx = d) Babybett vgl.. --J-sm y. 52° La rotation Autour du Punkt R est donnÃ©e par la diffÃ©rentielle dx de l'Angle ein. Ces deux mouv

. Comptes Rendus hebdomadaires des sÃ© ances de l'AcadÃ©mie des Sciences. Wissenschaft - Gesellschaften, etc.; Wissenschaft; Wissenschaft. SÃANCE DU 0,4 FÃVRIER 1902. 461 comme inconnues. Pour qu'il en soit Ainsi, il faut et Il suffit que les coeffi-Kunden R. r,, B-pg, R;/,. RxyÂ "S vÃ©rifient Les cinq Beziehungen suivantes: (>) dy dp-O DJ'S, - Dy d dpd &Lt;i-d-S dy dp-Ã'-S DX d'i4-dy dx^- dqdy dq-djc DP "Ces Bedingungen Ã©tant supposÃ © es vÃ©rifiÃ © es, les Ã © quations (4) admettent une infinitÃ © mes de Lösungen que l'auf obtiendra Gleichheit des Quadra-Taufers de systÃ¨. Si/,, f ^.^ fiyf forment un premier systÃ¨me de s Stockfoto

RMRECYJK–. Comptes Rendus hebdomadaires des sÃ© ances de l'AcadÃ©mie des Sciences. Wissenschaft - Gesellschaften, etc.; Wissenschaft; Wissenschaft. SÃANCE DU 0,4 FÃVRIER 1902. 461 comme inconnues. Pour qu'il en soit Ainsi, il faut et Il suffit que les coeffi-Kunden R. r,, B-pg, R;/,. RxyÂ "S vÃ©rifient Les cinq Beziehungen suivantes: (>) dy dp-O DJ'S, - Dy d dpd &Lt;i-d-S dy dp-Ã'-S DX d'i4-dy dx^- dqdy dq-djc DP "Ces Bedingungen Ã©tant supposÃ © es vÃ©rifiÃ © es, les Ã © quations (4) admettent une infinitÃ © mes de Lösungen que l'auf obtiendra Gleichheit des Quadra-Taufers de systÃ¨. Si/,, f ^.^ fiyf forment un premier systÃ¨me de s

$. Acta Societatis Scientiarum Fennicae. Wissenschaft. Ueber Arheitsgrossen in der mathematischen Physik. 15 (53) = - dC Z = - yd^l J , (a), - § 2 + y2 fii2ly T^'?^^^^^^^ x + y '-P'. (j4r'(x-i)^g fij. {X+ly + tf Mann hat dabei^X dl {x - 1) 2 - I - J/2 21^(a; - 0^ + 2/*' dy dx; (a;+^) 2+y2;. | (^. ?) 2+y2j-Sterben Grössen EIN' und Y sind die partiellen Ableitungen der Funktion (54) f (x,,,) =?L* £ ", tgJ-j. rf |+ C=- ^' £ arctg^^ j2x2/(II T J) 2+y 2^(a;-|)+C=C== (ii Arc tg ein: "2/^P fltX arctg 2" 2/Mann sieht aus dem Integralausdrucke von F{x, y) sowie aus dem ausgeführten Werte, dass F{x, y) um i^r/ii Zuni Stockfoto$

RMRR3RCR–. Acta Societatis Scientiarum Fennicae. Wissenschaft. Ueber Arheitsgrossen in der mathematischen Physik. 15 (53) = - dC Z = - yd^l J , (a), - § 2 + y2 fii2ly T^'?^^^^^^^ x + y '-P'. (j4r'(x-i)^g fij. {X+ly + tf Mann hat dabei^X dl {x - 1) 2 - I - J/2 21^(a; - 0^ + 2/*' dy dx; (a;+^) 2+y2;. | (^. ?) 2+y2j-Sterben Grössen EIN' und Y sind die partiellen Ableitungen der Funktion (54) f (x,,,) =?L* £ ", tgJ-j. rf |+ C=- ^' £ arctg^^ j2x2/(II T J) 2+y 2^(a;-|)+C=C== (ii Arc tg ein: "2/^P fltX arctg 2" 2/Mann sieht aus dem Integralausdrucke von F{x, y) sowie aus dem ausgeführten Werte, dass F{x, y) um i^r/ii Zuni

Analyselemente, die auf die Mechanik von Technik und Maschinen angewendet werden. Eine Funktion oder abscissaAM=x^ Abb. 9 und 10 der entsprechenden Kurve müssen um eine infinitesimale Magnitude MN^ erhöht werden, die wir durch 9^ infundieren, die entsprechende abhängige Variable, orordinate MP = y, geht in NQ^y^^ über und erhöht sich um den infini-tesimalen Wert B Q = NQ - MP, der mit dy gekennzeichnet werden soll. Beide Inkremente dx und dy von x und y werden als Differentiale, Orelemente der Variablen oder Koordinate x und y bezeichnet, und es ist jetzt unsere oberste Aufgabe zu finden, um am häufigsten wiederkehrende zu finden Stockfoto

RM2AWFAEX–Analyselemente, die auf die Mechanik von Technik und Maschinen angewendet werden. Eine Funktion oder abscissaAM=x^ Abb. 9 und 10 der entsprechenden Kurve müssen um eine infinitesimale Magnitude MN^ erhöht werden, die wir durch 9^ infundieren, die entsprechende abhängige Variable, orordinate MP = y, geht in NQ^y^^ über und erhöht sich um den infini-tesimalen Wert B Q = NQ - MP, der mit dy gekennzeichnet werden soll. Beide Inkremente dx und dy von x und y werden als Differentiale, Orelemente der Variablen oder Koordinate x und y bezeichnet, und es ist jetzt unsere oberste Aufgabe zu finden, um am häufigsten wiederkehrende zu finden

Es wird auf das Textbuch der Mechanik verwiesen. Jetzt ein differentielles Element, dx dy dz, im verastelten Körper, wie in Abb. dargestellt, vorstellen. 67. Lassen Sie die Schrägseile über die verschiedenen Flächen parallel zu den Bezugsachsen in Konponenten auflösen, dann müssen die sechssmöglichen Schrägsichtespannungen durch die in Abb. gezeigten achtzehn normalen und schierenden Spannungen dargestellt werden. 67. Die bei der Kennzeichnung dieser numerischen Spannungen verwendete Notation lautet wie folgt: Zuerst ist zu beachten, dass ein doppeltes Tiefgestellt verwendet wird. Der erste dieser Tiefpunkte stimmt immer mit dem Namen der Achse überein, zu der die Ebene, über die der Stressauftritt i, steht Stockfoto

RM2AX0DC1–Es wird auf das Textbuch der Mechanik verwiesen. Jetzt ein differentielles Element, dx dy dz, im verastelten Körper, wie in Abb. dargestellt, vorstellen. 67. Lassen Sie die Schrägseile über die verschiedenen Flächen parallel zu den Bezugsachsen in Konponenten auflösen, dann müssen die sechssmöglichen Schrägsichtespannungen durch die in Abb. gezeigten achtzehn normalen und schierenden Spannungen dargestellt werden. 67. Die bei der Kennzeichnung dieser numerischen Spannungen verwendete Notation lautet wie folgt: Zuerst ist zu beachten, dass ein doppeltes Tiefgestellt verwendet wird. Der erste dieser Tiefpunkte stimmt immer mit dem Namen der Achse überein, zu der die Ebene, über die der Stressauftritt i, steht

RM2ANF41P–Mechanik der engineeringComprising Statik und Dynamik von Festkörpern: und die Mechanik der Werkstoffe von Konstruktionen oder Festigkeit und Elastizität der Träger, Säulen, Bögen, Wellen, etc. o ein Paar, und somit die Summe ihres Momente ist die gleiche genommen um jede Achse unabhängig | auf der Ebene des Paares (§ 32).] Die a> Anti-Derivat der Mitgliedstaaten (1), Eip=P (y 2 ix-y2x>) +3 fcX-y2p (ix-y2x>). (2) Ein x (die Konstante nicht ausgedrückt, als er null ist). Jetzt fromsymmetry wissen wir, dass die Tangente an die Kurve 0 Bat B horizontal ist, d. h., für x = Yi, dy-7-dx = 0, und Thesevalues in eq. (

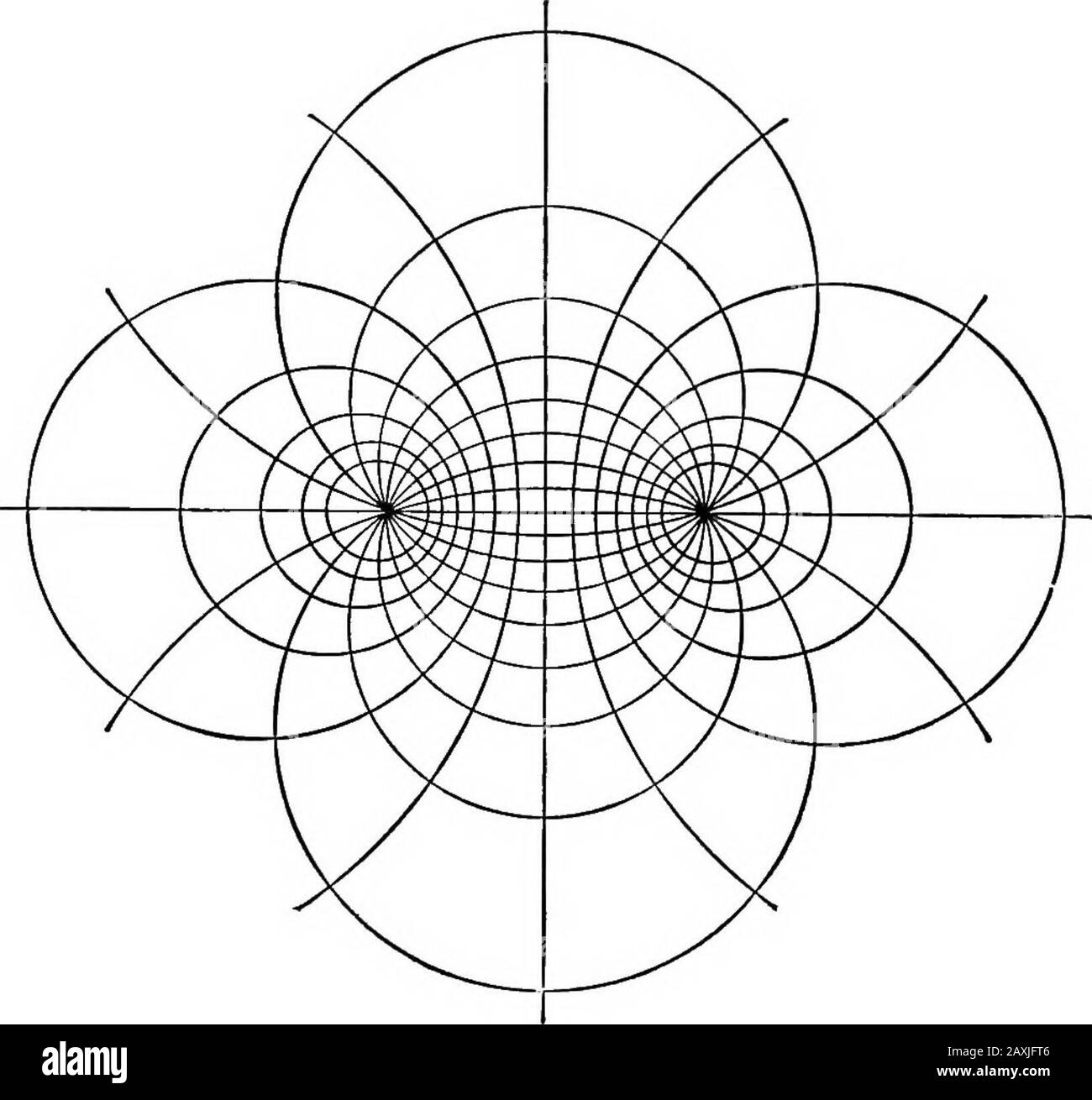$Ein elementarer Ablauf von Infinitesimalberechnungen . Dies stellt ein System von rechteckigen Hyperbolas dar, deren Axesübereinkommen in Richtung der Asymptome des früheren Systems. Z. B. 2. So finden Sie die Kurven orthogonal zu den Kreisen a? + f + 2i.y-¥ = Q (8), wobei /a der variable Parameter ist.Difierentiating, wir haben xdx + {y + ij) dy = 0, und deshalb, für die Bahn, xdy - {y + It) dx = Q.EUminating /x, zwischen diesem und (8), finden wir 2xy^ + {a? (^ 9-l) Oder x^^-y^-o^ + k (10). Dies ist linear, mit y^ als unabhängiger Variable. Der integrierte Faktor, wie in der Regel des Art. 177, OR Stockfoto$

RM2AXJFT6–Ein elementarer Ablauf von Infinitesimalberechnungen . Dies stellt ein System von rechteckigen Hyperbolas dar, deren Axesübereinkommen in Richtung der Asymptome des früheren Systems. Z. B. 2. So finden Sie die Kurven orthogonal zu den Kreisen a? + f + 2i.y-¥ = Q (8), wobei /a der variable Parameter ist.Difierentiating, wir haben xdx + {y + ij) dy = 0, und deshalb, für die Bahn, xdy - {y + It) dx = Q.EUminating /x, zwischen diesem und (8), finden wir 2xy^ + {a? (^ 9-l) Oder x^^-y^-o^ + k (10). Dies ist linear, mit y^ als unabhängiger Variable. Der integrierte Faktor, wie in der Regel des Art. 177, OR

Eine elementare Abhandlung über Differentialgleichungen und deren Anwendungen. esented durch die komplette Primitiv. Durch einen Graphen veranschaulichen. 9. Grafische Darstellung. Wir werden nun einige examplesof eine Methode * schnell skizzieren die allgemeine Form der Familie von Kurven, die die komplette Primitive? Ich - • * Aufgrund von Dr. S. und Prof. Brodetsky Takeo Wada. Differentialgleichungen, wobei f (x, y) ist eine Funktion von x und y in einem perfekt definitefinite Wert * für jedes Paar von endlichen Werte von x und y. Die Kurven der Familie sind die Merkmale von theequation genannt. dy Ex. (I) Hier dx= Stockfoto

RM2ANA6KW–Eine elementare Abhandlung über Differentialgleichungen und deren Anwendungen. esented durch die komplette Primitiv. Durch einen Graphen veranschaulichen. 9. Grafische Darstellung. Wir werden nun einige examplesof eine Methode * schnell skizzieren die allgemeine Form der Familie von Kurven, die die komplette Primitive? Ich - • * Aufgrund von Dr. S. und Prof. Brodetsky Takeo Wada. Differentialgleichungen, wobei f (x, y) ist eine Funktion von x und y in einem perfekt definitefinite Wert * für jedes Paar von endlichen Werte von x und y. Die Kurven der Familie sind die Merkmale von theequation genannt. dy Ex. (I) Hier dx=

$Analyselemente, die auf die Mechanik von Maschinen und Maschinen angewendet werden. M N X A. M N Dies ist die allgemeinste Regel für die Bestimmung der unterschiedlichen Funktion, von der durch Anwendung auf verschiedene Funktionen andere Regeln mehr oder weniger allgemein abgeleitet werden können. Wenn wir beispielsweise y = ^^ haben, dann dy = (x-{-dxy - ^^, oder, da wir (x -^- dxy = x ^^^- 2xdx -J-^ müssen, ergibt sich dy = 2xdx + dx = (2x + 8 ) dx; c 6 ANALYSELEMENTE. [Art. 6. Oder mehr einfach, da dx als infinitesimal verschwindet, wenn mit 2 a verglichen wird;: Dy = d{xy = 2xdoc, y=:x^ entspricht dem a Stockfoto$

RM2AWFA8W–Analyselemente, die auf die Mechanik von Maschinen und Maschinen angewendet werden. M N X A. M N Dies ist die allgemeinste Regel für die Bestimmung der unterschiedlichen Funktion, von der durch Anwendung auf verschiedene Funktionen andere Regeln mehr oder weniger allgemein abgeleitet werden können. Wenn wir beispielsweise y = ^^ haben, dann dy = (x-{-dxy - ^^, oder, da wir (x -^- dxy = x ^^^- 2xdx -J-^ müssen, ergibt sich dy = 2xdx + dx = (2x + 8 ) dx; c 6 ANALYSELEMENTE. [Art. 6. Oder mehr einfach, da dx als infinitesimal verschwindet, wenn mit 2 a verglichen wird;: Dy = d{xy = 2xdoc, y=:x^ entspricht dem a

Eine elementare Abhandlung über Differentialgleichungen und deren Anwendungen. Fia. 4. dessen Produkt-1, d. h., dass Sie senkrecht stehen. Die char-acteristics sind daher Kreise der Radius mit dem Ursprung als Zentrum. * Siehe Papier, grafische Lösung von Prof. Takeo Wada, Memoiren des theCollege von Wissenschaft, Kyoto Imperial University, Vol. II. Nr. 3, Juli 1917. Grafische Darstellung In diesem Fall den singulären Punkt kann als ein Kreis mit Radius Null betrachtet werden, denn die Begrenzung der Form der Merkmale in der Nähe von Es, aber keine charakteristischen offinite Größe durchläuft. dy y-kx dx x+ky Schreiben dy Stockfoto

RM2ANA4J8–Eine elementare Abhandlung über Differentialgleichungen und deren Anwendungen. Fia. 4. dessen Produkt-1, d. h., dass Sie senkrecht stehen. Die char-acteristics sind daher Kreise der Radius mit dem Ursprung als Zentrum. * Siehe Papier, grafische Lösung von Prof. Takeo Wada, Memoiren des theCollege von Wissenschaft, Kyoto Imperial University, Vol. II. Nr. 3, Juli 1917. Grafische Darstellung In diesem Fall den singulären Punkt kann als ein Kreis mit Radius Null betrachtet werden, denn die Begrenzung der Form der Merkmale in der Nähe von Es, aber keine charakteristischen offinite Größe durchläuft. dy y-kx dx x+ky Schreiben dy

$Analyselemente, die auf die Mechanik von Technik und Maschinen angewendet werden. Ation y = x^^ nur in ihren entgegengesetzten Positionen in Bezug auf die Achse der Abscissas XX^ und bilden die symme-trischen Hälften eines ganzen. Art. 10. Aus der wichtigen Formel d {oo^) = nx^^dx folgt daraus auch die Formel für den tangentialen Winkel der entsprechenden Kurven, wie in Abb. dargestellt. 18; wir haben, nämlich: Dy - tana, a = ^-- = nx^ - ^ dx und damit die Subtangente dieser Kurven: DX x^ X dy n x^ nThere ist dementsprechend für NeiVs parabola, deren Gleichung Vx^a • ist. 1 ^(^) " 1^ .a 3J^a tang, A = ^ &g Stockfoto$

RM2AWF9GP–Analyselemente, die auf die Mechanik von Technik und Maschinen angewendet werden. Ation y = x^^ nur in ihren entgegengesetzten Positionen in Bezug auf die Achse der Abscissas XX^ und bilden die symme-trischen Hälften eines ganzen. Art. 10. Aus der wichtigen Formel d {oo^) = nx^^dx folgt daraus auch die Formel für den tangentialen Winkel der entsprechenden Kurven, wie in Abb. dargestellt. 18; wir haben, nämlich: Dy - tana, a = ^-- = nx^ - ^ dx und damit die Subtangente dieser Kurven: DX x^ X dy n x^ nThere ist dementsprechend für NeiVs parabola, deren Gleichung Vx^a • ist. 1 ^(^) " 1^ .a 3J^a tang, A = ^ &g

Eine Untersuchung der Ausbreitung, Brechung, Reflexion, Interferenz und Beugung von Wellen Wellen. Die zwei Röhren. Eine modifizierte Form der Waetzmans Apparate Verwendung vom Autor in der vorliegenden Untersuchung verwendet werden. II DIGCUSSIO ^ ich OP DIE THEORIE DER RIPPLESThe Gleichung der Kontinuität. - In der studyingthe Eulerian Methode der Bewegung von Fluiden, Aufmerksamkeit ist fest auf einen bestimmten pointP = (x, y, z, t). Angenommen, P (Abb. 1) Zu einem solchen Punkt surrounde 1 durch eine kleine rechteckige Element dx dy Dz. Die Bewegung statt, die in der folgenden Weise ausgedrückt werden können. Lassen Sie u, v und w repräsentieren die Velocity componen Stockfoto

RM2AKG531–Eine Untersuchung der Ausbreitung, Brechung, Reflexion, Interferenz und Beugung von Wellen Wellen. Die zwei Röhren. Eine modifizierte Form der Waetzmans Apparate Verwendung vom Autor in der vorliegenden Untersuchung verwendet werden. II DIGCUSSIO ^ ich OP DIE THEORIE DER RIPPLESThe Gleichung der Kontinuität. - In der studyingthe Eulerian Methode der Bewegung von Fluiden, Aufmerksamkeit ist fest auf einen bestimmten pointP = (x, y, z, t). Angenommen, P (Abb. 1) Zu einem solchen Punkt surrounde 1 durch eine kleine rechteckige Element dx dy Dz. Die Bewegung statt, die in der folgenden Weise ausgedrückt werden können. Lassen Sie u, v und w repräsentieren die Velocity componen

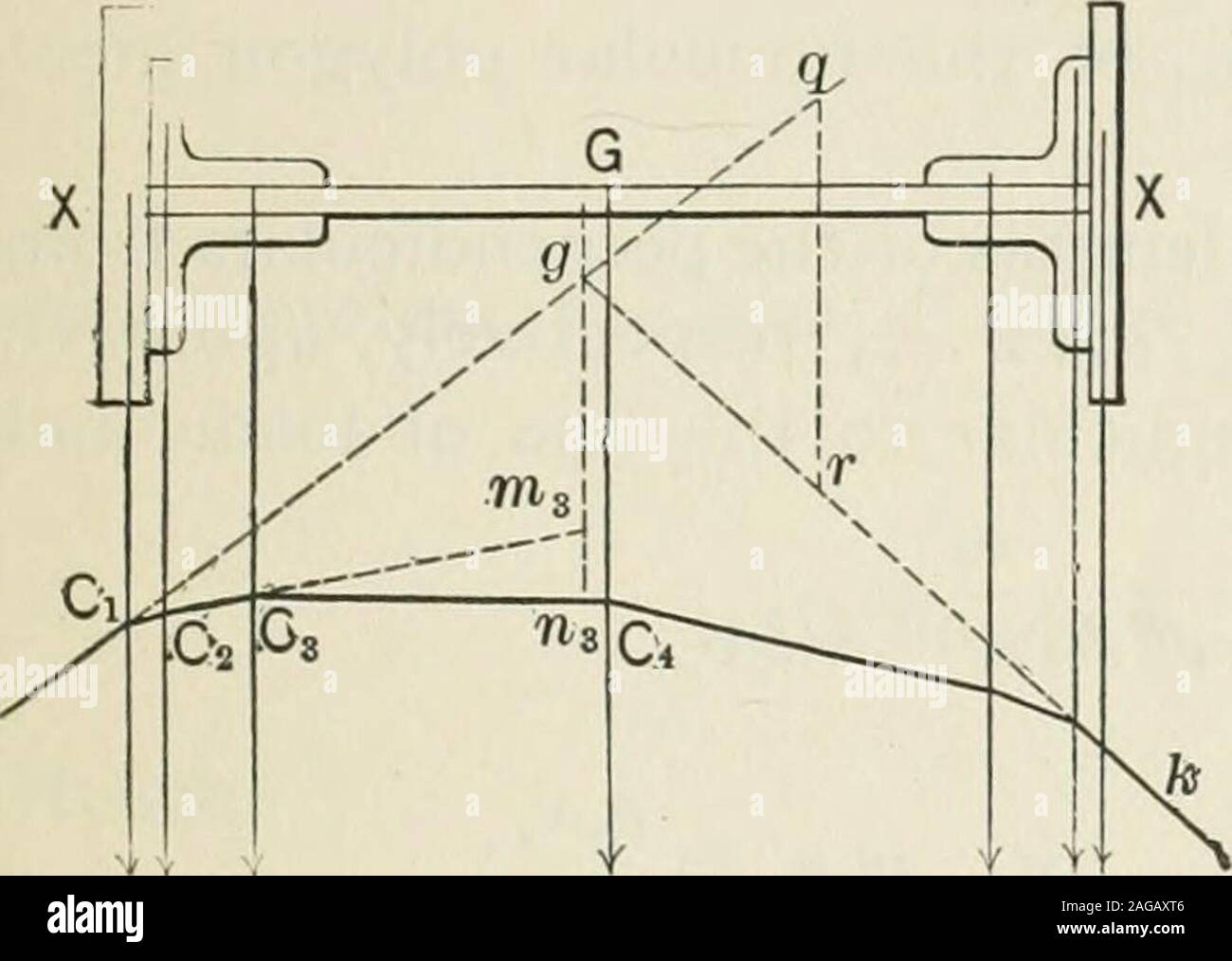$. Theorie der Strukturen und Festigkeit der Materialien. Abb. 14. Abb. ist. Lassen Sie 7 ich die Linie von Lasten und OS, OT er die radiallines von O, der Pole, parallel zu den Tangenten an P und Q EINE als Ursprung. Lassen Sie 0 die Neigung der Tangente an P sein, um den Strahl und die Polar Abstand OV: =/>. Wdx = die Last auf den Teil iMN. Dann Wdx = ST = SF-TV=6-p p Tan Tan{6-|-dO) = - Pdd, etwa. dy dx zweimal smce dxIntegrating, Py =-Z/^ ^-^+c, x+c^, t und c^ werden Konstanten von Integration. 6 =^ dx-ZENTREN DER SCHWERKRAFT. II Wenn die Intensität, w, der Last konstant ist, wxpy Stockfoto$

RM2AGAXT6–. Theorie der Strukturen und Festigkeit der Materialien. Abb. 14. Abb. ist. Lassen Sie 7 ich die Linie von Lasten und OS, OT er die radiallines von O, der Pole, parallel zu den Tangenten an P und Q EINE als Ursprung. Lassen Sie 0 die Neigung der Tangente an P sein, um den Strahl und die Polar Abstand OV: =/>. Wdx = die Last auf den Teil iMN. Dann Wdx = ST = SF-TV=6-p p Tan Tan{6-|-dO) = - Pdd, etwa. dy dx zweimal smce dxIntegrating, Py =-Z/^ ^-^+c, x+c^, t und c^ werden Konstanten von Integration. 6 =^ dx-ZENTREN DER SCHWERKRAFT. II Wenn die Intensität, w, der Last konstant ist, wxpy

Analyselemente, die auf die Mechanik von Technik und Maschinen angewendet werden. Kranker Anstieg um i? ^ = 8?/, und s, durch das Element P Q::= 8s; und wir haben gemäß dem pythagoreischen Theorem PQ = PP + Q R i. e.: 8s^ = dx + 8?/;daher 86 = ydx- - dy und consequentlj^, den Bogen selbst; S Vdx 4- dy Art. 32.] ELEMENTE DER ANALYSE. 49 Zum Beispiel Für Neivs Parabel^ (yici. Art. 9, Abb. 1 * 1,) deren Äqua-tion ay- = x^ ist, haben wir 2aydy = Sxdx; daher: Nach welcher SX^dx , ^ , 9 x dxand. CY^ = 2 ay 4: A^ y^ 4:a (^ + ia) ^^ ^ -/^+^>-?/o+^D(^ -1) zu finden ^ Stockfoto

RM2AWEYFH–Analyselemente, die auf die Mechanik von Technik und Maschinen angewendet werden. Kranker Anstieg um i? ^ = 8?/, und s, durch das Element P Q::= 8s; und wir haben gemäß dem pythagoreischen Theorem PQ = PP + Q R i. e.: 8s^ = dx + 8?/;daher 86 = ydx- - dy und consequentlj^, den Bogen selbst; S Vdx 4- dy Art. 32.] ELEMENTE DER ANALYSE. 49 Zum Beispiel Für Neivs Parabel^ (yici. Art. 9, Abb. 1 * 1,) deren Äqua-tion ay- = x^ ist, haben wir 2aydy = Sxdx; daher: Nach welcher SX^dx , ^ , 9 x dxand. CY^ = 2 ay 4: A^ y^ 4:a (^ + ia) ^^ ^ -/^+^>-?/o+^D(^ -1) zu finden ^

$Die Encyclopedia Britannica; ein Wörterbuch der Künste, Wissenschaften und allgemeine literatureWith neue Karten und original amerikanischen Artikel von bedeutenden writersWith amerikanischen Korrekturen und Ergänzungen, die jedem Volume auf dem neuesten Stand. Abgelehnt. Dann haben wir, nach dem Ablauf der Zeit<, x = k ^^GT) y=/2 gkt S Elimiiiating t, haben wir die Gleichung der Parabel Pfad-zu den orthogonalen Flugbahn (Meridian Abschnitt der Oberfläche von Equ. U Aktion), differenzieren finden, gesetzt - somit haben dy y y ^ x+y-JX-y dx 2 k X + V * -- y^s/x+y+Va;-y oder -/l^j{Dx - dy) + s/7^j{Dx - dy) 0, 80, dass {x + yf ± {x - y) i=const. Stockfoto$

RM2ANAMT3–Die Encyclopedia Britannica; ein Wörterbuch der Künste, Wissenschaften und allgemeine literatureWith neue Karten und original amerikanischen Artikel von bedeutenden writersWith amerikanischen Korrekturen und Ergänzungen, die jedem Volume auf dem neuesten Stand. Abgelehnt. Dann haben wir, nach dem Ablauf der Zeit<, x = k ^^GT) y=/2 gkt S Elimiiiating t, haben wir die Gleichung der Parabel Pfad-zu den orthogonalen Flugbahn (Meridian Abschnitt der Oberfläche von Equ. U Aktion), differenzieren finden, gesetzt - somit haben dy y y ^ x+y-JX-y dx 2 k X + V * -- y^s/x+y+Va;-y oder -/l^j{Dx - dy) + s/7^j{Dx - dy) 0, 80, dass {x + yf ± {x - y) i=const.

Analyselemente, die auf die Mechanik von Maschinen und Maschinen angewendet werden. M Ndy dx sin. A = -- und cos. A = -; und weiter OS CS dy ^ = j t/ 1 + tang. -^-d x =j^^^^ =j ^^^. Wenn nun die Gleichung zwischen zwei der Größen x, y, s und abe gegeben ist, können wir dann auch Gleichungen zwischen zwei anderen dieser Größen finden. Wenn wir zum Beispiel cos. A =- haben. , VC--s gibt es auch; ex = OS COS. A = du und J l/c -4- s -^ Vc 4- s -^ Vu ^ Vc + 50 ANALYSEELEMENTE. [Art. 33. = ^/c^ -f s^ -f- con.; und wenn x und s gleichzeitig null sind: X == Vc^ H- s - c Art. 33. Eine gerade Linie an Stockfoto

RM2AWEY1H–Analyselemente, die auf die Mechanik von Maschinen und Maschinen angewendet werden. M Ndy dx sin. A = -- und cos. A = -; und weiter OS CS dy ^ = j t/ 1 + tang. -^-d x =j^^^^ =j ^^^. Wenn nun die Gleichung zwischen zwei der Größen x, y, s und abe gegeben ist, können wir dann auch Gleichungen zwischen zwei anderen dieser Größen finden. Wenn wir zum Beispiel cos. A =- haben. , VC--s gibt es auch; ex = OS COS. A = du und J l/c -4- s -^ Vc 4- s -^ Vu ^ Vc + 50 ANALYSEELEMENTE. [Art. 33. = ^/c^ -f s^ -f- con.; und wenn x und s gleichzeitig null sind: X == Vc^ H- s - c Art. 33. Eine gerade Linie an

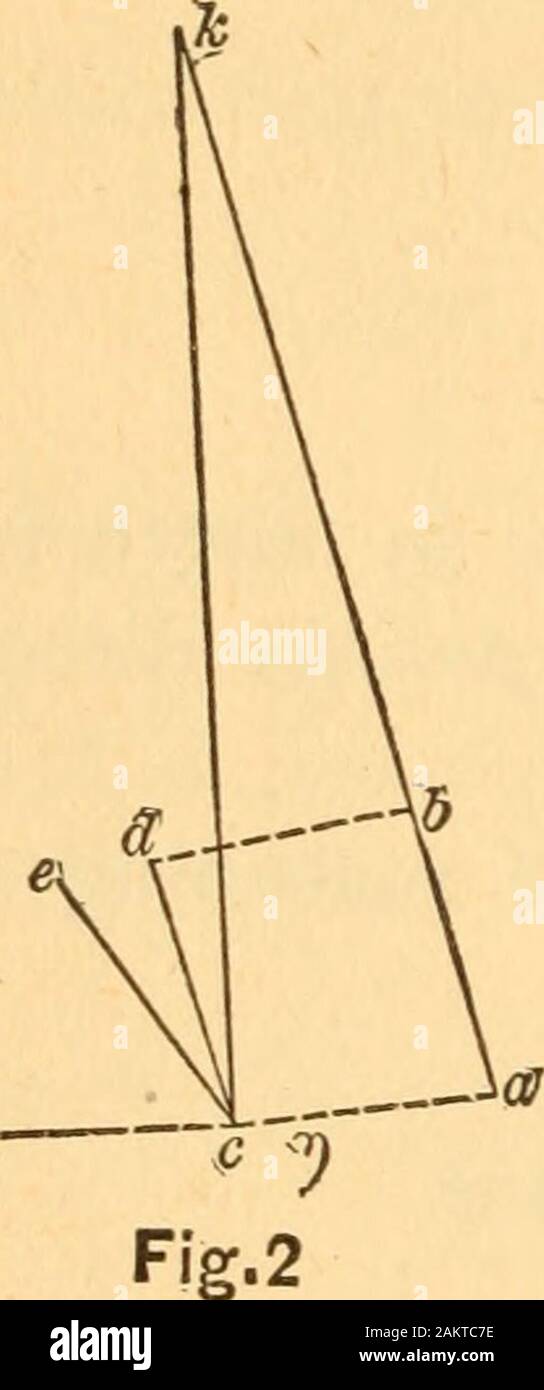Die Elastizität und Beständigkeit der Materialien von Engineering. nd die Begründung verbunden mit der obigen Gleichung, geben wird: dw drf p00 tan ^ dz r cos tp dcp r r Ohne Erklärung kann es auf einmal geschrieben werden: dv dpdy dr Abb. Ich Dieses, und Abb. 2 der vorstehenden Art geben: dti dco, dv-dp1=- TT- und - dy Dr r dx r dip Diese sind in den Ausdruck für T^r^ Preciselythe gleichen Feigen und Methode verwendet werden: dv dp dw drf tj ^ dz r cos ip-Dcp-dj/dr r, die bei der Suche nach T^r* 3 34 Elastizität in amorpher Festkörper verwendet werden sollen. [Art. 8. Der Ausdruck für -^- 7. Stockfoto

RM2AKTC7E–Die Elastizität und Beständigkeit der Materialien von Engineering. nd die Begründung verbunden mit der obigen Gleichung, geben wird: dw drf p00 tan ^ dz r cos tp dcp r r Ohne Erklärung kann es auf einmal geschrieben werden: dv dpdy dr Abb. Ich Dieses, und Abb. 2 der vorstehenden Art geben: dti dco, dv-dp1=- TT- und - dy Dr r dx r dip Diese sind in den Ausdruck für T^r^ Preciselythe gleichen Feigen und Methode verwendet werden: dv dp dw drf tj ^ dz r cos ip-Dcp-dj/dr r, die bei der Suche nach T^r* 3 34 Elastizität in amorpher Festkörper verwendet werden sollen. [Art. 8. Der Ausdruck für -^- 7.

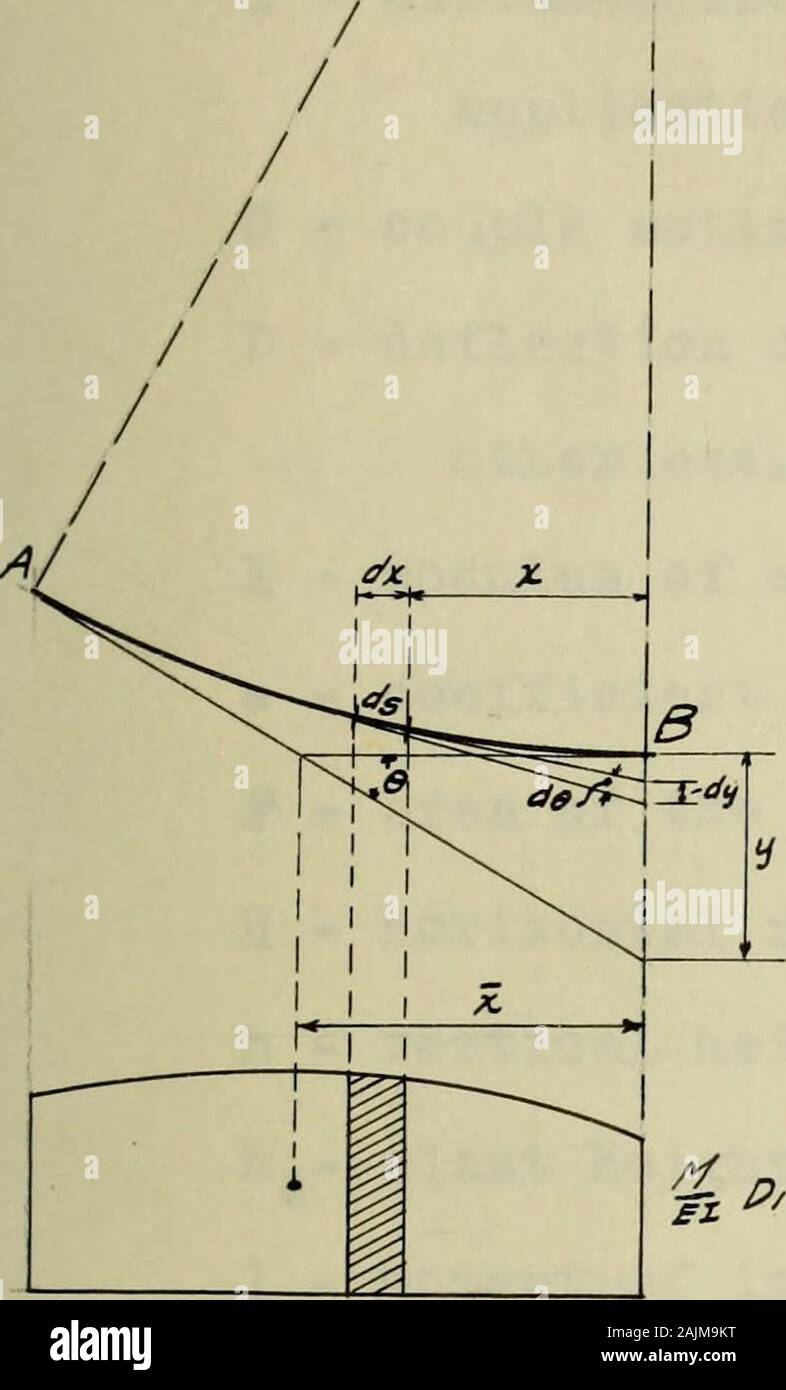Statisch unbestimmt betont in steifen gerahmte Strukturen. gerader Balken groß ist, kann es FiS-II - 10. Angenommen, dass dx ist gleich ds. Dann 0 ICH dx.. In Abb. 12 Die Kurve AB rep-nimmt die elastischen Kurve einer por- tion des Strahls. Durch die geometryof der Abbildung, dy-x d 9 oder, dy-Mx ds EI vorausgesetzt, dass dx= ds, gibt dy s Mx dxEI oder, y = (Mx dx EI? g-z P/o#rarn. ft?. 2 - Jetzt der schattigen elementaren Bereich der m/EI Schaltplan auf Mdx/EI gleich; und die gesamte EREA angestrebt des Diagramms ist gleich/M dxJA EI Das statische Moment der schattierte Bereich um den Punkt B ist equalto x" Mdx/EI; und die statica Stockfoto

RM2AJM9KT–Statisch unbestimmt betont in steifen gerahmte Strukturen. gerader Balken groß ist, kann es FiS-II - 10. Angenommen, dass dx ist gleich ds. Dann 0 ICH dx.. In Abb. 12 Die Kurve AB rep-nimmt die elastischen Kurve einer por- tion des Strahls. Durch die geometryof der Abbildung, dy-x d 9 oder, dy-Mx ds EI vorausgesetzt, dass dx= ds, gibt dy s Mx dxEI oder, y = (Mx dx EI? g-z P/o#rarn. ft?. 2 - Jetzt der schattigen elementaren Bereich der m/EI Schaltplan auf Mdx/EI gleich; und die gesamte EREA angestrebt des Diagramms ist gleich/M dxJA EI Das statische Moment der schattierte Bereich um den Punkt B ist equalto x" Mdx/EI; und die statica

. "Traité de Mécanique céleste. orps solides, et sert à définir les. Il en résulte que pourléquilibre dune Masse fluide, chaque molécule doit être en équi-libre En vertu de la Kräfte qui sollicitent, et des Druck quelleéprouve de la Part des Molécules environnantes. Développons leséquations qui résultent de cette Propriété. Pour Cela, considérons Un système de molécules Fluides für-mant un petit infiniment parallélipipède Rechteck. Soient x, y, z, les Trois coordonnées Rechtecke de langle de ce parallélipipède, le plus Voisin de lorigine des coordonnées. Soient dx, dy, dz, les trois Dim Stockfoto

RM2AG2D9M–. "Traité de Mécanique céleste. orps solides, et sert à définir les. Il en résulte que pourléquilibre dune Masse fluide, chaque molécule doit être en équi-libre En vertu de la Kräfte qui sollicitent, et des Druck quelleéprouve de la Part des Molécules environnantes. Développons leséquations qui résultent de cette Propriété. Pour Cela, considérons Un système de molécules Fluides für-mant un petit infiniment parallélipipède Rechteck. Soient x, y, z, les Trois coordonnées Rechtecke de langle de ce parallélipipède, le plus Voisin de lorigine des coordonnées. Soient dx, dy, dz, les trois Dim

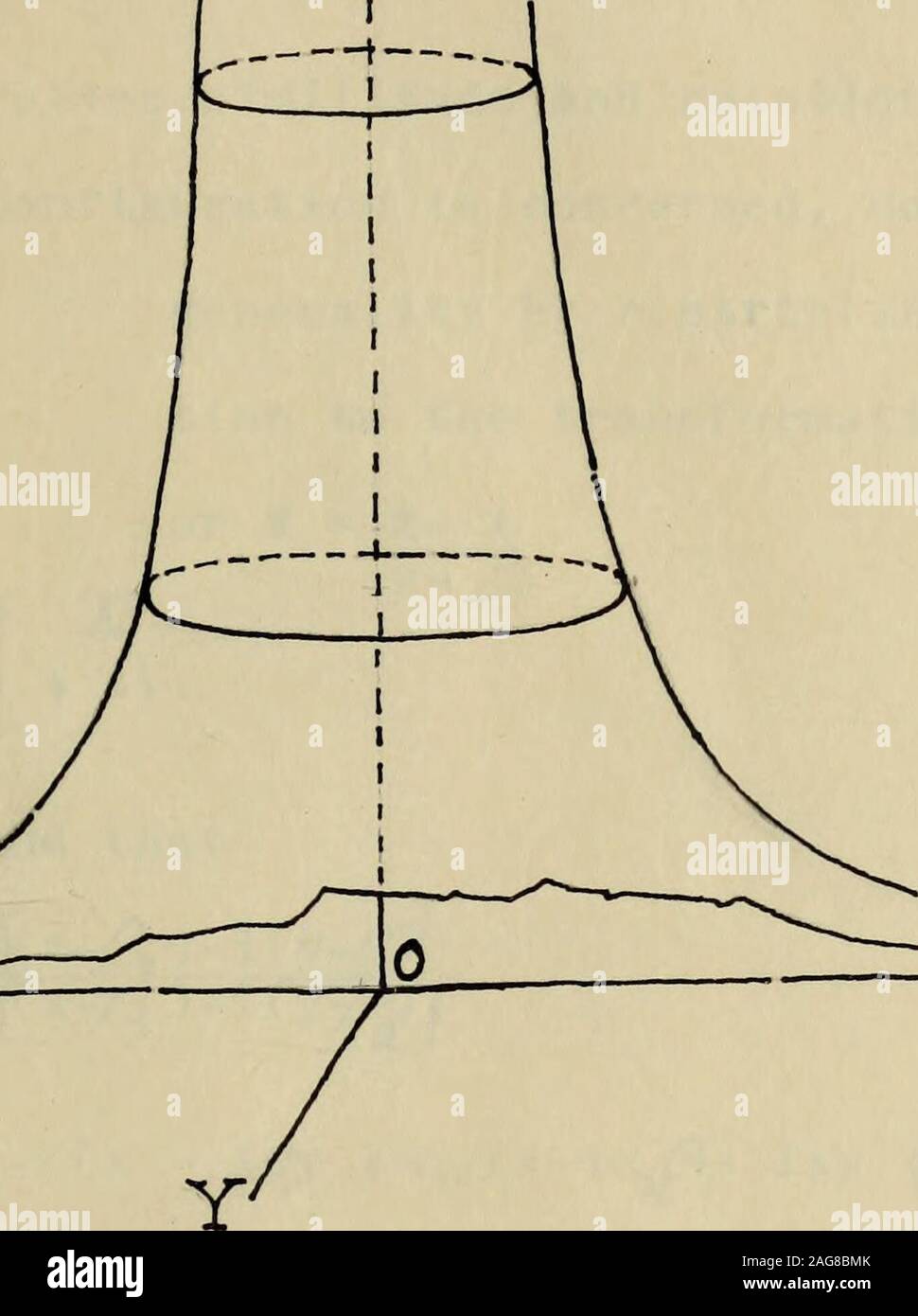. Auf absorbierenden Oberflächen Cauchy's. Er Locus. Von der Steigung der Tangente zu finden (1) im Punkt (x, o). dx ox ein y dx 13^y. d^f f dy ^-^ f-f^ dy Abl - " dy^-d r-V dx y-Substitution der Koordinaten der Doppel Punkt in diesem Equa-tion, nachdem man für x^x^jB = 12 x-Hx^6 X c) f = 4 xy-^? x y d = 4 x - 6 x. Oxoy erhalten wir dx = -4 v j^^ TlBy - (12 x-6x,) (4 x-fix.) 4x - 6x,-X. - X-X, 1, da dieser Wert ist die irr^abhängige des Iscation von Ti e Drucken o tanp: En-cy in Fsme-xz-Ebene, der tv: o Zweige der Kurve durch thedouhle Punkt in der xy-Projektion schneiden sich in einem konstanten Winkel. Zu fi Stockfoto

RM2AG8BMK–. Auf absorbierenden Oberflächen Cauchy's. Er Locus. Von der Steigung der Tangente zu finden (1) im Punkt (x, o). dx ox ein y dx 13^y. d^f f dy ^-^ f-f^ dy Abl - " dy^-d r-V dx y-Substitution der Koordinaten der Doppel Punkt in diesem Equa-tion, nachdem man für x^x^jB = 12 x-Hx^6 X c) f = 4 xy-^? x y d = 4 x - 6 x. Oxoy erhalten wir dx = -4 v j^^ TlBy - (12 x-6x,) (4 x-fix.) 4x - 6x,-X. - X-X, 1, da dieser Wert ist die irr^abhängige des Iscation von Ti e Drucken o tanp: En-cy in Fsme-xz-Ebene, der tv: o Zweige der Kurve durch thedouhle Punkt in der xy-Projektion schneiden sich in einem konstanten Winkel. Zu fi

. Die London, Edinburgh und Dublin philosophische Zeitschrift und Zeitschrift für Wissenschaft. Mit diesen durch die direkte Aktion der geladene Kugel), haben wir " e d 1* 47 r dx p = - i - 1 J 4 = IR-dy pj e d 147 r dz p daher d £ ep d 2 1 dt kirdxd^ pdg ep d 2 1 dt A.7 T D% dy p dh e d 2 1 % dt Airdtjdzp Auswirkungen, die durch die Bewegung der elektrifizierte Körper produziert. 231 Somit 4 f=* £ -# !, dt 4z7r dx2 pdg ep d 2 1 dt (1) 47 r dx dy pdh ep d 2 1 dt4 tt dx dz p J mit Maxwells Notation, F, G, H der componentsof der Vektor-Potential an irgendeinem Punkt werden; dann, byi Strom andMagnetism / § 616, F=fi Stockfoto

RM2AFT405–. Die London, Edinburgh und Dublin philosophische Zeitschrift und Zeitschrift für Wissenschaft. Mit diesen durch die direkte Aktion der geladene Kugel), haben wir " e d 1* 47 r dx p = - i - 1 J 4 = IR-dy pj e d 147 r dz p daher d £ ep d 2 1 dt kirdxd^ pdg ep d 2 1 dt A.7 T D% dy p dh e d 2 1 % dt Airdtjdzp Auswirkungen, die durch die Bewegung der elektrifizierte Körper produziert. 231 Somit 4 f=* £ -# !, dt 4z7r dx2 pdg ep d 2 1 dt (1) 47 r dx dy pdh ep d 2 1 dt4 tt dx dz p J mit Maxwells Notation, F, G, H der componentsof der Vektor-Potential an irgendeinem Punkt werden; dann, byi Strom andMagnetism / § 616, F=fi

Forhandlinger i Videnskabs-selskabet i Christiania . LAD (x,y,z) og {x,y,z) viere to tilsvarende punkter.Beskriver linjeelementet cfø, <%, (fø en kegleflade, vil den med CARL STØRMER. NOGLE GEOMETRISKE SATSER. [Nein 2. 1902.] so paralele vektor gjennem origo af enhedsfladen snitteud et fladestykke 8 og derved bestemme en rumsektor V. ligesaa kan V vaere den rumsektor som bestemmes afvektoren paralleles med linjeelementet (dx dy dz). Vor sats er da, bei F og V har samme volum. "VI kan ande satsen paa transformationes af et kurve-komplex bestaaende af oo3 kurver i rummet, f. ex. Integral-kurv. Stockfoto

RM2AX9P38–Forhandlinger i Videnskabs-selskabet i Christiania . LAD (x,y,z) og {x,y,z) viere to tilsvarende punkter.Beskriver linjeelementet cfø, <%, (fø en kegleflade, vil den med CARL STØRMER. NOGLE GEOMETRISKE SATSER. [Nein 2. 1902.] so paralele vektor gjennem origo af enhedsfladen snitteud et fladestykke 8 og derved bestemme en rumsektor V. ligesaa kan V vaere den rumsektor som bestemmes afvektoren paralleles med linjeelementet (dx dy dz). Vor sats er da, bei F og V har samme volum. "VI kan ande satsen paa transformationes af et kurve-komplex bestaaende af oo3 kurver i rummet, f. ex. Integral-kurv.

Verschiedene Kollektionen von Smithsonian. dx dt dx 1 dp DFX HDF d?F du2 - = 2 CO sin 6 -- - k - - ^ . p dy dy dy dy dt dy folglich haben wir P - = 2 CO sn p dt P = 2 CO sin 6FX - KF - - - * W + C . . (6) Schreiben von x - £ = r sin <py - rj =? R cos <p 236 SMITHSONIAN MISCELLANEOUS COLLECTIONS und die Werte von F und Fv ersetzen wir P = [2 wsin 6 . N - km - M]lognat RP - [2 A) sin 0 . M + kN + N] <p MR - Nrj. MW + N?^ sin <p + - cos <p VOL. 51 (7) - U2 + C Die Bedingung, dass die Isobaren feste Kurven sind, erfordert, dass die Gleichung (7) von2wsmdM+kN+N = 0 (8) zeigt, dass die Stockfoto

RM2AWF87G–Verschiedene Kollektionen von Smithsonian. dx dt dx 1 dp DFX HDF d?F du2 - = 2 CO sin 6 -- - k - - ^ . p dy dy dy dy dt dy folglich haben wir P - = 2 CO sn p dt P = 2 CO sin 6FX - KF - - - * W + C . . (6) Schreiben von x - £ = r sin <py - rj =? R cos <p 236 SMITHSONIAN MISCELLANEOUS COLLECTIONS und die Werte von F und Fv ersetzen wir P = [2 wsin 6 . N - km - M]lognat RP - [2 A) sin 0 . M + kN + N] <p MR - Nrj. MW + N?^ sin <p + - cos <p VOL. 51 (7) - U2 + C Die Bedingung, dass die Isobaren feste Kurven sind, erfordert, dass die Gleichung (7) von2wsmdM+kN+N = 0 (8) zeigt, dass die

MÃ©moires couronnÃ©s et autres mÃ©moires publiÃ© s par l'AcadÃ©mie royale des Sciences, des Lettres et des beaux-arts de. puis jusquà x=0 x=r0 et négatives (Kräfte Attratives) depuis x = r 0 jusquà x = 00. Léquation ci-dessus (a), mise sous la forme entière yx * = r0-x, Montre que immédiatement les Achsen des coordonnées sind desasymptotes à la courbe. Différentions Deux Fois léquation (a); nous aurons Dy1 Dy6/2 r0 dx x * dxl x * x 1 (*) Extraits de partie des Comptes Rendus de deParis lAcadémie des sciences et des Mémoires de la Societe des Ingénieurs civils De Frankreich, déposés à la Biblio Stockfoto

RM2AKAB40–MÃ©moires couronnÃ©s et autres mÃ©moires publiÃ© s par l'AcadÃ©mie royale des Sciences, des Lettres et des beaux-arts de. puis jusquà x=0 x=r0 et négatives (Kräfte Attratives) depuis x = r 0 jusquà x = 00. Léquation ci-dessus (a), mise sous la forme entière yx * = r0-x, Montre que immédiatement les Achsen des coordonnées sind desasymptotes à la courbe. Différentions Deux Fois léquation (a); nous aurons Dy1 Dy6/2 r0 dx x * dxl x * x 1 (*) Extraits de partie des Comptes Rendus de deParis lAcadémie des sciences et des Mémoires de la Societe des Ingénieurs civils De Frankreich, déposés à la Biblio

Smithsonian Miseral Collections. G die Achsen 0 X, O Y und 0 Z nehmen die Form u = M y, V = M x und w = 0 ?] an), Die Diese Werte in Gleichungen (i) und (2) von §35 ersetzen, wir haben 1 dp - ? -,- = - 2 CO sin 6 M x - k M y - M2 x (2) p dx 1 dp - • -3- = 2 CO sin 6 • M y - k M x - M2 y (3) p dy By Integration wir finden P Po -- = -i x2 (2 CO sin 6 M +M2) - - - k M xy + hf (2 w sin 0 . M - M2) und durch die Einführung von 2 CO sin 6 tang A = K werden wir km, / M n.,/ M ??-j- y i tang o; - - I - 2 xy - X- tang A + 12 k I k 1 (4) M Wenn Tan A > -, dann die Isobaren, die durch Gleichung dargestellt werden (4 Stockfoto

RM2AWF6H6–Smithsonian Miseral Collections. G die Achsen 0 X, O Y und 0 Z nehmen die Form u = M y, V = M x und w = 0 ?] an), Die Diese Werte in Gleichungen (i) und (2) von §35 ersetzen, wir haben 1 dp - ? -,- = - 2 CO sin 6 M x - k M y - M2 x (2) p dx 1 dp - • -3- = 2 CO sin 6 • M y - k M x - M2 y (3) p dy By Integration wir finden P Po -- = -i x2 (2 CO sin 6 M +M2) - - - k M xy + hf (2 w sin 0 . M - M2) und durch die Einführung von 2 CO sin 6 tang A = K werden wir km, / M n.,/ M ??-j- y i tang o; - - I - 2 xy - X- tang A + 12 k I k 1 (4) M Wenn Tan A > -, dann die Isobaren, die durch Gleichung dargestellt werden (4

$. Angewandte Kalkül; Grundsätze und Anwendungen . , , )dy -r {uy , , , )dz+ * ABLEITUNG VON [i] 39 das Differential des Produkts einer beliebigen Anzahl von Variablen ist die Summe der Produkte der Differential von jedem durch alle die Weste .^^, ,(N DDN-NDD[VI] dl^^j = ^ der Unterschied eines Bruchs ist der Nenner durch den Unterschied des Zählers minus dem Zähler durch den Unterschied des Nenners, geteilt durch das Quadrat des Nenners. nx dx. [VII] d(x^) das Differenzial einer Variablen mit einem konstanten Exponenten ist das Produkt des Exponenten und der Variablen mit dem Exponenten lessone durch t Stockfoto$

RM2CGH9D1–. Angewandte Kalkül; Grundsätze und Anwendungen . , , )dy -r {uy , , , )dz+ * ABLEITUNG VON [i] 39 das Differential des Produkts einer beliebigen Anzahl von Variablen ist die Summe der Produkte der Differential von jedem durch alle die Weste .^^, ,(N DDN-NDD[VI] dl^^j = ^ der Unterschied eines Bruchs ist der Nenner durch den Unterschied des Zählers minus dem Zähler durch den Unterschied des Nenners, geteilt durch das Quadrat des Nenners. nx dx. [VII] d(x^) das Differenzial einer Variablen mit einem konstanten Exponenten ist das Produkt des Exponenten und der Variablen mit dem Exponenten lessone durch t

. Eine elementare Abhandlung über die Differential-und Integralrechnung. M M M NT ABB. 6 die wir dy erhalten = in Bezug auf dx als Konstante, wir * wenn die Variable um gleiche Schritte zunimmt, d.h. wenn das Differential konstant ist, wird die Variable eine gleichwertige Variable genannt. n BEISPIELE. Haben mm, MM, MM als die aufeinanderfolgenden gleichen Inkremengevon x9 oder dxs; Während wir von Abb. 7 dass RP, RP, RP oder die dy% nicht mehr gleich sind, aber verringern, wie wir uns in Richtung theright bewegen, und daher ist die Differenz zwischen zwei aufeinanderfolgenden dys anegative Menge (daran erinnernd, dass die Differenz immer byta gefunden wird Stockfoto

RM2CEDM6W–. Eine elementare Abhandlung über die Differential-und Integralrechnung. M M M NT ABB. 6 die wir dy erhalten = in Bezug auf dx als Konstante, wir * wenn die Variable um gleiche Schritte zunimmt, d.h. wenn das Differential konstant ist, wird die Variable eine gleichwertige Variable genannt. n BEISPIELE. Haben mm, MM, MM als die aufeinanderfolgenden gleichen Inkremengevon x9 oder dxs; Während wir von Abb. 7 dass RP, RP, RP oder die dy% nicht mehr gleich sind, aber verringern, wie wir uns in Richtung theright bewegen, und daher ist die Differenz zwischen zwei aufeinanderfolgenden dys anegative Menge (daran erinnernd, dass die Differenz immer byta gefunden wird

. Eine elementare Abhandlung über die Differential-und Integralrechnung. (Siehe Mathematical Visitor, 1878, S. 26.) 208. Gemischtes Koordinatensystem. – anstatt einen Körper in Spalten zu teilen, die auf rechteckigen Basen stehen, so dass z dx dy das Volumen der Infinitesimalsäule ist, Es ist manchmal bequemer, es in infinitesimale Spalten zu teilen, die auf dem polaren Element von Area abed = r dr dd stehen, in diesem Fall wird das entsprechende Parallelopipedon durch zr dr dd dargestellt, und der Ausdruck für V wird. Abb. 59. V = J Jzr dr do, aufgenommen zwischen den richtigen Grenzen. Aus der Gleichung der Oberfläche, Stockfoto

RM2CEDGKH–. Eine elementare Abhandlung über die Differential-und Integralrechnung. (Siehe Mathematical Visitor, 1878, S. 26.) 208. Gemischtes Koordinatensystem. – anstatt einen Körper in Spalten zu teilen, die auf rechteckigen Basen stehen, so dass z dx dy das Volumen der Infinitesimalsäule ist, Es ist manchmal bequemer, es in infinitesimale Spalten zu teilen, die auf dem polaren Element von Area abed = r dr dd stehen, in diesem Fall wird das entsprechende Parallelopipedon durch zr dr dd dargestellt, und der Ausdruck für V wird. Abb. 59. V = J Jzr dr do, aufgenommen zwischen den richtigen Grenzen. Aus der Gleichung der Oberfläche,

. Differential- und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. Iry2Ax = 7r lim V 2/2Az. n=oo a 7l = oo ■ Unser fundamentaler Satz ist hier anwendbar, und wir haben (A) V=7r£y2dx, das ist die Formel für das Volumen eines Festkörpers der Revolution. In §176 FLÄCHEN UND FESTKÖRPER DER UMDREHUNG 255 kann man ähnlich zeigen, dass das Volumen des Festkörpers, der durch Drehen um OY erzeugt wird, das kurvenviereckige aAEb (A) ■r x2dy ist. Die Elemente des Volumens in (A) und (A) sind jeweils iry2Ax und irx2Ay oder iry2 dx und irx2 dy.176. Bereiche der Oberflächen der Revolution. Let Stockfoto

RM2CEJD6T–. Differential- und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. Iry2Ax = 7r lim V 2/2Az. n=oo a 7l = oo ■ Unser fundamentaler Satz ist hier anwendbar, und wir haben (A) V=7r£y2dx, das ist die Formel für das Volumen eines Festkörpers der Revolution. In §176 FLÄCHEN UND FESTKÖRPER DER UMDREHUNG 255 kann man ähnlich zeigen, dass das Volumen des Festkörpers, der durch Drehen um OY erzeugt wird, das kurvenviereckige aAEb (A) ■r x2dy ist. Die Elemente des Volumens in (A) und (A) sind jeweils iry2Ax und irx2Ay oder iry2 dx und irx2 dy.176. Bereiche der Oberflächen der Revolution. Let

. Eine elementare Abhandlung über die Differential-und Integralrechnung. Erential der ersten Differential ist die zweite differenzial, vertreten durch d2y, dhi, etc., und lesen, secondary Differential von y etc. Das Differential der zweiten dif-ferential ist die dritte Differential, vertreten durch d3y, d?U, etc., Und lesen, dritte Differential von y, etc. In wie man-ner, haben wir die vierte, fünfte, etc., Differentiale. So gewonnene Differentiale werden sukzessive Differentiale genannt. So soll ab eine rechte Linie sein, deren Gleichung y = ax + B.- ist. dy = adx. Betrachten Sie DX nun als konstant, d. h., lassen Sie x equicres-cen sein Stockfoto

RM2CEDM8J–. Eine elementare Abhandlung über die Differential-und Integralrechnung. Erential der ersten Differential ist die zweite differenzial, vertreten durch d2y, dhi, etc., und lesen, secondary Differential von y etc. Das Differential der zweiten dif-ferential ist die dritte Differential, vertreten durch d3y, d?U, etc., Und lesen, dritte Differential von y, etc. In wie man-ner, haben wir die vierte, fünfte, etc., Differentiale. So gewonnene Differentiale werden sukzessive Differentiale genannt. So soll ab eine rechte Linie sein, deren Gleichung y = ax + B.- ist. dy = adx. Betrachten Sie DX nun als konstant, d. h., lassen Sie x equicres-cen sein

. Die Straßenbahn Zeitschrift . 26 und enthielten Abb. 1 bis 10- der dritte Teil, 9. August, und enthielt Fig. 11 bis 13, und der vierte Teil, Aug 16 und enthielt Abb. 14. dy o – = – = tan o = V – zerodx dx das heißt, null Geschwindigkeit, d. h. absolute Ruhe. Eine Kurve wie in Abb. 15 ist in Wirklichkeit eine Distanz-Zeitkurve, wird aber meist einfach als Distanzkurve bezeichnet. Aus der vorhergehenden Analyse wird man leicht erkennen, daß die Steigung der Krümmungsbewegung oder der Winkel, den sie mit der Achse von x macht, ein Indiz und Maß für die Geschwindigkeit des sich bewegenden Körpers ist. Es ist auch eine Indikation des d Stockfoto

RM2CH33DH–. Die Straßenbahn Zeitschrift . 26 und enthielten Abb. 1 bis 10- der dritte Teil, 9. August, und enthielt Fig. 11 bis 13, und der vierte Teil, Aug 16 und enthielt Abb. 14. dy o – = – = tan o = V – zerodx dx das heißt, null Geschwindigkeit, d. h. absolute Ruhe. Eine Kurve wie in Abb. 15 ist in Wirklichkeit eine Distanz-Zeitkurve, wird aber meist einfach als Distanzkurve bezeichnet. Aus der vorhergehenden Analyse wird man leicht erkennen, daß die Steigung der Krümmungsbewegung oder der Winkel, den sie mit der Achse von x macht, ein Indiz und Maß für die Geschwindigkeit des sich bewegenden Körpers ist. Es ist auch eine Indikation des d

. Angewandte Kalkül; Prinzipien und Anwendungen . Formeln geben die Volumen generatedby eine vollständige Revolution des Bereichs. Folge. - Wenn die Achse der Revolution schneidet den Bereich, (1) oder (2) wird die Differenz zwischen den Volumina durch die beiden Teile generiert. Daher F = 0, wenn diese beiden Teile gleiche Volumen erzeugen. Integration (1) zuerst mit respectto y, und (2) zuerst mit Bezug auf x, die oberen Grenzen bei den Variablen y oder x und die unteren Grenzen Null, gibt y = ^ r^y^dx (10 ^ Xo und y = 7r / x^dy, (20 die Formeln für soHds der Revolution, Single Integration. 169. Bände von Triple Integrati Stockfoto

RM2CJ8079–. Angewandte Kalkül; Prinzipien und Anwendungen . Formeln geben die Volumen generatedby eine vollständige Revolution des Bereichs. Folge. - Wenn die Achse der Revolution schneidet den Bereich, (1) oder (2) wird die Differenz zwischen den Volumina durch die beiden Teile generiert. Daher F = 0, wenn diese beiden Teile gleiche Volumen erzeugen. Integration (1) zuerst mit respectto y, und (2) zuerst mit Bezug auf x, die oberen Grenzen bei den Variablen y oder x und die unteren Grenzen Null, gibt y = ^ r^y^dx (10 ^ Xo und y = 7r / x^dy, (20 die Formeln für soHds der Revolution, Single Integration. 169. Bände von Triple Integrati

. Eine elementare Abhandlung über die Differential-und Integralrechnung. Cant eines Bogens ist gleich der Sezant des gleichen Bogens, in die Tangentof des Bogens, in die Differential des Bogens. 29. Y - cosec als zu unterscheiden. Wir haben y = csec x = sec (90 Grad - x). .-. dy = d s (90 Grad - x) = s (90 Grad - x) tan (90 Grad - x) d (90 Grad - x)= – COsec x COT x dx. Daher ist das Differenzial des Kosekans eines Bogens negativ und gleich dem Kosekant des Bogens, in den Kotangent des Bogens, in das Differenzial des Bogens. 30. Y = vers als zu unterscheiden. Wir haben y = vers x = 1 – cos x, . dy = d (1 – cos x) = si Stockfoto

RM2CEDMEE–. Eine elementare Abhandlung über die Differential-und Integralrechnung. Cant eines Bogens ist gleich der Sezant des gleichen Bogens, in die Tangentof des Bogens, in die Differential des Bogens. 29. Y - cosec als zu unterscheiden. Wir haben y = csec x = sec (90 Grad - x). .-. dy = d s (90 Grad - x) = s (90 Grad - x) tan (90 Grad - x) d (90 Grad - x)= – COsec x COT x dx. Daher ist das Differenzial des Kosekans eines Bogens negativ und gleich dem Kosekant des Bogens, in den Kotangent des Bogens, in das Differenzial des Bogens. 30. Y = vers als zu unterscheiden. Wir haben y = vers x = 1 – cos x, . dy = d (1 – cos x) = si

. Eine elementare Abhandlung über die Differential- und Integralrechnung. Als, und daher kann sev-ax eral-Werte nicht haben, es sei denn, indem wir die Form annehmen -• Daher haben wir -f- = - oder -=- = 0, und - = 0, fromdx 0 dx dy, die kritischen Werte von x und y zu bestimmen. Wenn diese Werte von z und y aus -j- = 0 und -=- = 0 realJ dx dy und satisfy (1) sind, können sie zu einem Mehrpunkt gehören. Wenn y nur einen Wert für den entsprechenden Wert von % hat und auf beiden Seiten zwei oder mehr reale Werte, ist dieser Punkt ein Mehrpunkt. Wir Werten dann -y- = - aus, und ji gibt es mehrere reale und ungleiche Werte Stockfoto

RM2CEDK3T–. Eine elementare Abhandlung über die Differential- und Integralrechnung. Als, und daher kann sev-ax eral-Werte nicht haben, es sei denn, indem wir die Form annehmen -• Daher haben wir -f- = - oder -=- = 0, und - = 0, fromdx 0 dx dy, die kritischen Werte von x und y zu bestimmen. Wenn diese Werte von z und y aus -j- = 0 und -=- = 0 realJ dx dy und satisfy (1) sind, können sie zu einem Mehrpunkt gehören. Wenn y nur einen Wert für den entsprechenden Wert von % hat und auf beiden Seiten zwei oder mehr reale Werte, ist dieser Punkt ein Mehrpunkt. Wir Werten dann -y- = - aus, und ji gibt es mehrere reale und ungleiche Werte

. Eine elementare Abhandlung über die Differential-und Integralrechnung. + rfy – (z + ffe). (2) Wenn wir (1) von (2) abziehen, haben wir du = dv + dy - dz, (3) das erforderliche Differenzial. Daher ist das Differential der algebraischen Summe von einer beliebigen Anzahl von Funktionen gefunden wird, indem man die alge-braic Summe ihrer Differentiale. 15. Y = Axt unterscheiden ± B. (1) Geben Sie x das infinitesimal increment dx, und lassen Sie dy bethe entsprechenden infinitesimal increment von y aufgrund derincrement, die x nimmt. Dann (1) wird y + dy = a (x + dx) ± 0- (2) Subtrahieren (1) von (2), erhalten wir dy = adx, (3) das ist die Stockfoto

RM2CEDMH9–. Eine elementare Abhandlung über die Differential-und Integralrechnung. + rfy – (z + ffe). (2) Wenn wir (1) von (2) abziehen, haben wir du = dv + dy - dz, (3) das erforderliche Differenzial. Daher ist das Differential der algebraischen Summe von einer beliebigen Anzahl von Funktionen gefunden wird, indem man die alge-braic Summe ihrer Differentiale. 15. Y = Axt unterscheiden ± B. (1) Geben Sie x das infinitesimal increment dx, und lassen Sie dy bethe entsprechenden infinitesimal increment von y aufgrund derincrement, die x nimmt. Dann (1) wird y + dy = a (x + dx) ± 0- (2) Subtrahieren (1) von (2), erhalten wir dy = adx, (3) das ist die

. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung . Pposition, wir haben 1 + ^dxj dx und, durch (2), reduziert sich dies auf dx dx dx • • d^idx dv dydx dx a / i ax dy woher, Durch die Ersetzung des Wertes von ^, abgeleitet von dx, die letzte dieser Gleichungen, Eq. 1 wird y dv . V ^= -^ [x - ia). dfi Diese Beziehungen zeigen, dass die Tangente zur Evolute ein Nor-mal zum entsprechenden Punkt der Evolvente und dem Kontravers ist. Eine Folge dieser Eigenschaft ist, dass die Evolution einer Kurve der Ort der Schnittpunkte der konsekutiven Normalen zu dieser Kurve ist. Für die twon nehmen Stockfoto

RM2CHC0P2–. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung . Pposition, wir haben 1 + ^dxj dx und, durch (2), reduziert sich dies auf dx dx dx • • d^idx dv dydx dx a / i ax dy woher, Durch die Ersetzung des Wertes von ^, abgeleitet von dx, die letzte dieser Gleichungen, Eq. 1 wird y dv . V ^= -^ [x - ia). dfi Diese Beziehungen zeigen, dass die Tangente zur Evolute ein Nor-mal zum entsprechenden Punkt der Evolvente und dem Kontravers ist. Eine Folge dieser Eigenschaft ist, dass die Evolution einer Kurve der Ort der Schnittpunkte der konsekutiven Normalen zu dieser Kurve ist. Für die twon nehmen

$. Smithsonian verschiedene Sammlungen. Grob die aufeinander folgenden Punkt und die vorwärts Terminus, aber nicht im Allgemeinen durch den Anfangspunkt. Wenn wir dann in (5) (xlt yv zt) durch (x + dx, y + dy,z -f- dz) ersetzen, haben wir: 0 = [(&- y) dx – 02 – *) dy] j£)+ [.{z2 – z)dy –(y2 – y)dz][J^j + [C»2 – *) dz – (z2 –^*) (SH* durch die Gleichung der Fläche (1) und ihre Differenzgleichung kann eine der Variablen mit ihrem Differential eliminiert werden.die resultierende Differentialgleichung, die so integriert wird, dass der Startpunkt (XY, yv zx) enthalten ist, wird die Gleichung eines PR sein Stockfoto$

RM2CEXKRE–. Smithsonian verschiedene Sammlungen. Grob die aufeinander folgenden Punkt und die vorwärts Terminus, aber nicht im Allgemeinen durch den Anfangspunkt. Wenn wir dann in (5) (xlt yv zt) durch (x + dx, y + dy,z -f- dz) ersetzen, haben wir: 0 = [(&- y) dx – 02 – *) dy] j£)+ [.{z2 – z)dy –(y2 – y)dz][J^j + [C»2 – *) dz – (z2 –^*) (SH* durch die Gleichung der Fläche (1) und ihre Differenzgleichung kann eine der Variablen mit ihrem Differential eliminiert werden.die resultierende Differentialgleichung, die so integriert wird, dass der Startpunkt (XY, yv zx) enthalten ist, wird die Gleichung eines PR sein

. Eine elementare Abhandlung über die Differential- und Integralrechnung. Rivativ von Dydx oder , ist negativ. dx2 in der gleichen Weise, wenn die Kurve nach unten konvex ist, siehe Abb. 22, es ist klar, dass als x steigt, ein in-Falten, und daher tan ein in-Falten; das heißt, wie x steigt, dy Feige. 21 (Art 12.) dx erhöht sich, und damit die de-. Rivative von - orax Abb. 22. Y^ ist positiv, daher ist die Kurve konkav oder konvex nach unten, je nachdem, wie dx* oder +, 192 P OLAR CO- ODER DIN A TES ist. Dies zeigt sich auch in Abb. 23, wobei MM = MM= dx; PP den beiden Kurven und dem commontangent gemeinsam ist. PE = PR = dx; A Stockfoto

RM2CEDKAR–. Eine elementare Abhandlung über die Differential- und Integralrechnung. Rivativ von Dydx oder , ist negativ. dx2 in der gleichen Weise, wenn die Kurve nach unten konvex ist, siehe Abb. 22, es ist klar, dass als x steigt, ein in-Falten, und daher tan ein in-Falten; das heißt, wie x steigt, dy Feige. 21 (Art 12.) dx erhöht sich, und damit die de-. Rivative von - orax Abb. 22. Y^ ist positiv, daher ist die Kurve konkav oder konvex nach unten, je nachdem, wie dx* oder +, 192 P OLAR CO- ODER DIN A TES ist. Dies zeigt sich auch in Abb. 23, wobei MM = MM= dx; PP den beiden Kurven und dem commontangent gemeinsam ist. PE = PR = dx; A

. Eine elementare Abhandlung über die Differential-und Integralrechnung. om M in Richtung Dythe rechts. Wenn in einer Kurve y ?-- eine negative Menge ist, bedeutet dies, dass N links von M liegt, und wie in diesem Fall dxy j-r auch negativ ist, so liegt T rechts von M EXAMPLES. 1. Finde die Werte der Subtangente, Subnormal und senkrecht vom Ursprung auf der Tangente, in der Ellipse dy b2x hier --, = r-- dx A?y dx A^ti ^ also die Subtangente = y -=-, = - -j, dy W die Subnormale = y --f = - 2 x;ax a BEISPIELE. 177 die Senkrechte vom Ursprung auf Tangent2. Suchen Sie die Subtangente und die Subnormale zum C Stockfoto

RM2CEDKPX–. Eine elementare Abhandlung über die Differential-und Integralrechnung. om M in Richtung Dythe rechts. Wenn in einer Kurve y ?-- eine negative Menge ist, bedeutet dies, dass N links von M liegt, und wie in diesem Fall dxy j-r auch negativ ist, so liegt T rechts von M EXAMPLES. 1. Finde die Werte der Subtangente, Subnormal und senkrecht vom Ursprung auf der Tangente, in der Ellipse dy b2x hier --, = r-- dx A?y dx A^ti ^ also die Subtangente = y -=-, = - -j, dy W die Subnormale = y --f = - 2 x;ax a BEISPIELE. 177 die Senkrechte vom Ursprung auf Tangent2. Suchen Sie die Subtangente und die Subnormale zum C

$. Angewandte Kalkül; Grundsätze und Anwendungen . E^, y, die Funktion, ist die kunstvolle, entspricht der Steigung am Ende der Ordinate, und kann die Gesamtfläche unter der Kurve bis zur Ordinate darstellen. (Siehe Art. 138.) 131. Austausch von Grenzen. - seit dem definitiven Integral X f(x)dx = F(b)-F(a); daraus folgt, dass JF(x)dx=- i f (x) dx, da das zweite Element – [F (a) – F {b)]= F(h) – F(a) ist.daraus folgt auch, dass das definitive Integral eine Funktion seiner Grenzen ist, nicht seiner Variablen; Somit hat X / (y) dy den gleichen Wert wie / / (x) dx. Jedes ist F(b) - F(a). Das algebraische Zeichen eines bestimmten Integrals Stockfoto$

RM2CGGYYM–. Angewandte Kalkül; Grundsätze und Anwendungen . E^, y, die Funktion, ist die kunstvolle, entspricht der Steigung am Ende der Ordinate, und kann die Gesamtfläche unter der Kurve bis zur Ordinate darstellen. (Siehe Art. 138.) 131. Austausch von Grenzen. - seit dem definitiven Integral X f(x)dx = F(b)-F(a); daraus folgt, dass JF(x)dx=- i f (x) dx, da das zweite Element – [F (a) – F {b)]= F(h) – F(a) ist.daraus folgt auch, dass das definitive Integral eine Funktion seiner Grenzen ist, nicht seiner Variablen; Somit hat X / (y) dy den gleichen Wert wie / / (x) dx. Jedes ist F(b) - F(a). Das algebraische Zeichen eines bestimmten Integrals

. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung. Variable z; dh, ändern Sie die unabhängige Variable fromz zu X. ans. 2(p (x, y) = -y .:, . ^^ ^^ dx d-y dx^ 14. Eliminieren Sie die beliebigen Funktionen aus dx ^ dxdy ^ dy- (/.f ^ dy DIFFERENTIALRECHNUNG. IPJ^E^T SEOOIsTX). GEOMETRISCHE ANWENDUNGEN. SCHNITTPUNKT-L-TANGENTEN, NOEMALS, SUBTANGENTEN UND SUBNORMALEN ZU EBENEN KURVEN. 14 il. Die Tangentiallinie zu einer Kurve an einem bestimmten Punkt ist die Begrenzungsposition einer Sekantenlinie, die durch diesen Punkt führt, oder es ist das, was die Sekantenlinie wird, wenn ein anderer von itspoints der Kreuzung mit Stockfoto

RM2CHCDCE–. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung. Variable z; dh, ändern Sie die unabhängige Variable fromz zu X. ans. 2(p (x, y) = -y .:, . ^^ ^^ dx d-y dx^ 14. Eliminieren Sie die beliebigen Funktionen aus dx ^ dxdy ^ dy- (/.f ^ dy DIFFERENTIALRECHNUNG. IPJ^E^T SEOOIsTX). GEOMETRISCHE ANWENDUNGEN. SCHNITTPUNKT-L-TANGENTEN, NOEMALS, SUBTANGENTEN UND SUBNORMALEN ZU EBENEN KURVEN. 14 il. Die Tangentiallinie zu einer Kurve an einem bestimmten Punkt ist die Begrenzungsposition einer Sekantenlinie, die durch diesen Punkt führt, oder es ist das, was die Sekantenlinie wird, wenn ein anderer von itspoints der Kreuzung mit

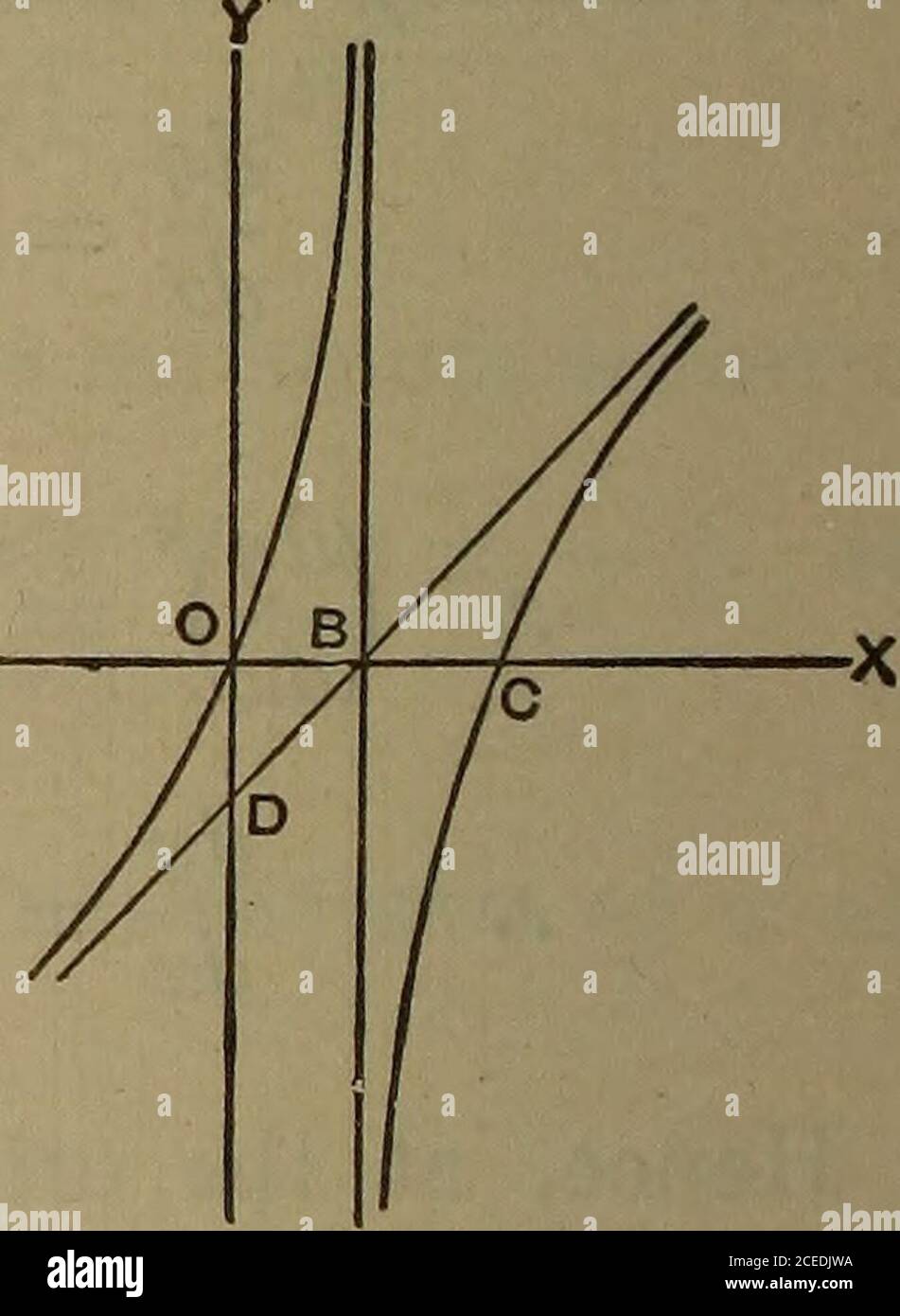. Eine elementare Abhandlung über die Differential-und Integralrechnung. Abb. 32.a etc. .«. Y = x – « ist die Gleichung des Asymptoten. Nehmen Sie daher ob = A = OD, und die Zeile BD producedis ist das Asymptote; nehmen Sie auch OC = 2a. Dann, da y = 0,beide, wenn # = 0 und x = 2«, schneidet die Kurve die Achse der x-BEISPIELE. 209 bei 0 und C. Zwischen 0 und B. die Kurve ist über der Achse ;bei B ist die Ordinate unendlich ; von B bis C ist die Kurve unterhalb; von C bis unendlich ist sie über OX. Wenn x negativ ist, ist y negativ; daher ist der Zweig links von0 vollständig unterhalb der Achse. dy x2 – 2ax 4- 2a2 auch DX (x Stockfoto

RM2CEDJWA–. Eine elementare Abhandlung über die Differential-und Integralrechnung. Abb. 32.a etc. .«. Y = x – « ist die Gleichung des Asymptoten. Nehmen Sie daher ob = A = OD, und die Zeile BD producedis ist das Asymptote; nehmen Sie auch OC = 2a. Dann, da y = 0,beide, wenn # = 0 und x = 2«, schneidet die Kurve die Achse der x-BEISPIELE. 209 bei 0 und C. Zwischen 0 und B. die Kurve ist über der Achse ;bei B ist die Ordinate unendlich ; von B bis C ist die Kurve unterhalb; von C bis unendlich ist sie über OX. Wenn x negativ ist, ist y negativ; daher ist der Zweig links von0 vollständig unterhalb der Achse. dy x2 – 2ax 4- 2a2 auch DX (x

. Die Straßenbahn Zeitschrift . (E)k Dies bedeutet, dass das Zeitelement dx, das der in-finitely kleinen Änderung in der Geschwindigkeit dy entspricht, dieser Änderung in der Geschwindigkeit multipliziert mit dem Kehrwert des Differentialkoeffizienten entspricht. Die totaltime x wäre, von (a) x = x + dx â¢ (f) solche Zeitinkrementwerte (dx) wären jedoch zu klein für die praktische Verwendung in der Darstellung von Kurven. Anmerkung.âThe erste Tranche dieses Papiers erschien im Street RailwayJournal Juli 5, und enthielt Figs. 1 bis 4; der zweite Teil, Juli 26, und mit Figuren. 5 bis 10; der dritte Teil, 9. August, und enthielt Fig. 11 bis 1 Stockfoto

RM2CH2YH5–. Die Straßenbahn Zeitschrift . (E)k Dies bedeutet, dass das Zeitelement dx, das der in-finitely kleinen Änderung in der Geschwindigkeit dy entspricht, dieser Änderung in der Geschwindigkeit multipliziert mit dem Kehrwert des Differentialkoeffizienten entspricht. Die totaltime x wäre, von (a) x = x + dx â¢ (f) solche Zeitinkrementwerte (dx) wären jedoch zu klein für die praktische Verwendung in der Darstellung von Kurven. Anmerkung.âThe erste Tranche dieses Papiers erschien im Street RailwayJournal Juli 5, und enthielt Figs. 1 bis 4; der zweite Teil, Juli 26, und mit Figuren. 5 bis 10; der dritte Teil, 9. August, und enthielt Fig. 11 bis 1

$. Differential- und Integralrechnung. - / = ^ -- ak. VI - ** V(i-^)3 .l{x + df ! X + a 34. Y =V/- - dy = (x – 2 A) V > s„dx. X – a y V V (# – «/ DIE TRIGONOMETRISCHEN FUNKTIONEN. 35. 7^ Differential des Sinus eines Winkels ist gleich dem Kosinus des Winkels in das Differential von ^ ^^ ? Der Winkel. Die Linie OP, als lineare Einheit genommen, um O als Achse nach oben drehend, soll einen beliebigen Winkel von POC haben; dann, inzirkuläres Maß, Länge von PC = U - Maß von POC. Wird die Länge U zu einer sich gleichmäßig verändernden Variable am Instant erreicht der Erzeugungspunkt die Position P, dann § 18, PT = Stockfoto$

RM2CEPG7N–. Differential- und Integralrechnung. - / = ^ -- ak. VI - ** V(i-^)3 .l{x + df ! X + a 34. Y =V/- - dy = (x – 2 A) V > s„dx. X – a y V V (# – «/ DIE TRIGONOMETRISCHEN FUNKTIONEN. 35. 7^ Differential des Sinus eines Winkels ist gleich dem Kosinus des Winkels in das Differential von ^ ^^ ? Der Winkel. Die Linie OP, als lineare Einheit genommen, um O als Achse nach oben drehend, soll einen beliebigen Winkel von POC haben; dann, inzirkuläres Maß, Länge von PC = U - Maß von POC. Wird die Länge U zu einer sich gleichmäßig verändernden Variable am Instant erreicht der Erzeugungspunkt die Position P, dann § 18, PT =

. Differential- und Integralrechnung. Abb. 27. (A) oder da sin a * dy ds vv*2 + dy* dxand cos a = – = dx ds -yjdx*1 + dy^ Diese Werte zusammen mit dem Wert von p ersetzt in (a) ergeben Krümmung Evolute und Involute 189 i + fdydy dx dx . x=x- – wf-1 – w dx* *-»+-^ •••••• w <fr2 2. Um die Gleichung der Evolute zu entstellen.Wenn wir jetzt mit (i) und (2) der Gleichung der Evolvente, y=A*) (3) kombinieren, um die variablen Koordinaten x und y der Evolvente zu eliminieren, werden wir eine resultierende Gleichung in xr und y haben. Die so gewonnene Gleichsetzung ist offensichtlich die des Evoluten. Um zu veranschaulichen, lasst uns Fi Stockfoto

RM2CEPERX–. Differential- und Integralrechnung. Abb. 27. (A) oder da sin a * dy ds vv*2 + dy* dxand cos a = – = dx ds -yjdx*1 + dy^ Diese Werte zusammen mit dem Wert von p ersetzt in (a) ergeben Krümmung Evolute und Involute 189 i + fdydy dx dx . x=x- – wf-1 – w dx* *-»+-^ •••••• w <fr2 2. Um die Gleichung der Evolute zu entstellen.Wenn wir jetzt mit (i) und (2) der Gleichung der Evolvente, y=A*) (3) kombinieren, um die variablen Koordinaten x und y der Evolvente zu eliminieren, werden wir eine resultierende Gleichung in xr und y haben. Die so gewonnene Gleichsetzung ist offensichtlich die des Evoluten. Um zu veranschaulichen, lasst uns Fi

. Eine elementare Abhandlung über die Differential-und Integralrechnung. Rivative von - orax Feige. 22. Y^ ist positiv, daher ist die Kurve konkav oder konvex nach unten, je nachdem, wie dx* oder +, 192 P OLAR CO- ODER DIN A TES ist. Dies zeigt sich auch in Abb. 23, wobei MM = MM= dx; PP den beiden Kurven und dem commontangent gemeinsam ist. PE = PR = dx; und PR = P2R, aber PR > P.2R > P,R.Jetzt sind PR und PR Konsekutivevalue von dy in der oberen Kurve, und PR und P,R sind konsekutiveTallies von dy in der unteren Kurve, und damit PR - PR = d (dy) = d2y is- und PJL - PR = d2y ist –; tatis, d2y ist – oder -f, entsprechend t Stockfoto

RM2CEDK89–. Eine elementare Abhandlung über die Differential-und Integralrechnung. Rivative von - orax Feige. 22. Y^ ist positiv, daher ist die Kurve konkav oder konvex nach unten, je nachdem, wie dx* oder +, 192 P OLAR CO- ODER DIN A TES ist. Dies zeigt sich auch in Abb. 23, wobei MM = MM= dx; PP den beiden Kurven und dem commontangent gemeinsam ist. PE = PR = dx; und PR = P2R, aber PR > P.2R > P,R.Jetzt sind PR und PR Konsekutivevalue von dy in der oberen Kurve, und PR und P,R sind konsekutiveTallies von dy in der unteren Kurve, und damit PR - PR = d (dy) = d2y is- und PJL - PR = d2y ist –; tatis, d2y ist – oder -f, entsprechend t

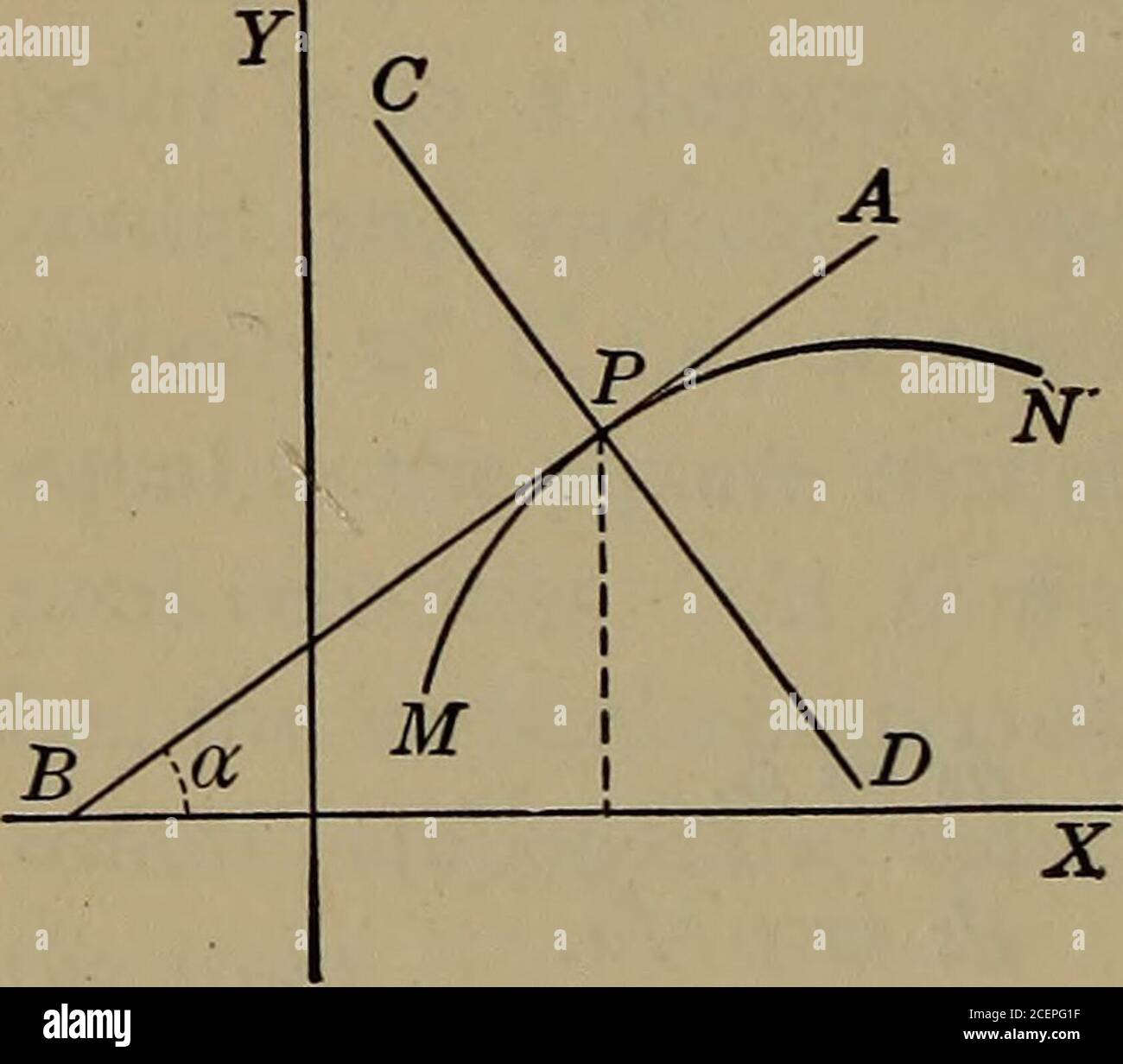. Differential- und Integralrechnung. t a bei O, y = 0 .-. Ay = 0, dx = 0, dk = 0. Bei A, y = : a .. dy = V, dx = V, ds = V V2. At£>,y = 2 a .. dy = 0, dx = 2 V, ds = 2 v. auch, ds f2ay chord PBV a BC = z>; Anmerkung. – das Cycloid genießt die mechanischen Eigenschaften des Seins der schnellste descetit und der gleichen titnes. Das Problem der Bestimmung der Linie der schnellsten Abstieg unter der Schwerkraft wurde vorgeschlagen, von John Bernouilliin 1696. Der Ursprung der Variationsrechnung kann auf dieses Problem zurückgeführt werden. Pascal wandte die Methode der Unteilbarkeit von Cavalieri mit emi-nent Erfolg auf die investigatio Stockfoto

RM2CEPG1F–. Differential- und Integralrechnung. t a bei O, y = 0 .-. Ay = 0, dx = 0, dk = 0. Bei A, y = : a .. dy = V, dx = V, ds = V V2. At£>,y = 2 a .. dy = 0, dx = 2 V, ds = 2 v. auch, ds f2ay chord PBV a BC = z>; Anmerkung. – das Cycloid genießt die mechanischen Eigenschaften des Seins der schnellste descetit und der gleichen titnes. Das Problem der Bestimmung der Linie der schnellsten Abstieg unter der Schwerkraft wurde vorgeschlagen, von John Bernouilliin 1696. Der Ursprung der Variationsrechnung kann auf dieses Problem zurückgeführt werden. Pascal wandte die Methode der Unteilbarkeit von Cavalieri mit emi-nent Erfolg auf die investigatio

. The Bell System technische Zeitschrift . l. Um dies zu zeigen, betrachten wir einen kleinen Würfel, der an einem Ende und mit einer bräunlichen Kraft am anderen befestigt ist. Die Kraft bewirkt, dass sich die obere Fläche in Bezug auf die untere Fläche, wie in Abb. 14, und eine Scherung S wird im Material aufgebaut, dessen Wert F = FXS dx dij (5) entspricht, wobei dx und dy die Querschnittsabmessungen und Fi die Scherstifigkeit sind. In dieser Verschiebung Arbeit wird durch die seitliche VerdrängungII gleich W KUF (6) 488 DAS GLOCKENSYSTEM TECHNISCHE JOURNAL, MAI 1952 aber U die Verschiebung ist U = dudz dz - S dz (7) und hen Stockfoto

RM2CRTK9T–. The Bell System technische Zeitschrift . l. Um dies zu zeigen, betrachten wir einen kleinen Würfel, der an einem Ende und mit einer bräunlichen Kraft am anderen befestigt ist. Die Kraft bewirkt, dass sich die obere Fläche in Bezug auf die untere Fläche, wie in Abb. 14, und eine Scherung S wird im Material aufgebaut, dessen Wert F = FXS dx dij (5) entspricht, wobei dx und dy die Querschnittsabmessungen und Fi die Scherstifigkeit sind. In dieser Verschiebung Arbeit wird durch die seitliche VerdrängungII gleich W KUF (6) 488 DAS GLOCKENSYSTEM TECHNISCHE JOURNAL, MAI 1952 aber U die Verschiebung ist U = dudz dz - S dz (7) und hen

. Angewandte Kalkül; Grundsätze und Anwendungen . Anmerkung. - EINE vollständige Behandlung des Subjekts des Trägheitsmoments und des Trägheitsprodukts geht über den Rahmen dieses Buches hinaus. Was gegeben wurde, wurde für das Mostpart auf Bereiche beschränkt, da dieser Teil des Themas mehr unmittelbare Anwendung im Engineering hat. 350 INTEGRALRECHNUNG 186. Abzug der Formeln für das Trägheitsmoment. – 1. Rechteck aus Basis h und Höhe h: L = fy da = JBF dy = TV W. §)■=! Lab =^h--AA^j^ h¥ + bh hh ly = jx^da = r hx^dx = j¥h. bh wieder IAB = £bydy = ibhIx = TV^^ J =^ 6 ; für Quadrat. A Y f X-^-A -- - i . X B 2. T Stockfoto

RM2CJ7KRR–. Angewandte Kalkül; Grundsätze und Anwendungen . Anmerkung. - EINE vollständige Behandlung des Subjekts des Trägheitsmoments und des Trägheitsprodukts geht über den Rahmen dieses Buches hinaus. Was gegeben wurde, wurde für das Mostpart auf Bereiche beschränkt, da dieser Teil des Themas mehr unmittelbare Anwendung im Engineering hat. 350 INTEGRALRECHNUNG 186. Abzug der Formeln für das Trägheitsmoment. – 1. Rechteck aus Basis h und Höhe h: L = fy da = JBF dy = TV W. §)■=! Lab =^h--AA^j^ h¥ + bh hh ly = jx^da = r hx^dx = j¥h. bh wieder IAB = £bydy = ibhIx = TV^^ J =^ 6 ; für Quadrat. A Y f X-^-A -- - i . X B 2. T

. Eine elementare Abhandlung über die Differential-und Integralrechnung. 198 BEISPIELE. Daher ist es kein Mehrpunkt. Wenn x > oder yx Daher ist der Punkt der ersten Art, und die Tangentzur Kurve am Punkt machen mit der Achse von x Winkeln, deren Tangenten sind -f- ^/a und - Za- 2. Untersuchen Sie x* + 2ax2y - ayz = 0 für mehrere Punkte. Wir gehen nach der zweiten Methode vor, da alle kritischen Punkte in diesem Beispiel nicht leicht durch Prüfung zu finden sind. J = 4^ + «y) = 0; (1) 0 = B(A*-iy) ==; (2) dy 4#3 -f- 4:axy dx 3ay2 – 2ax2 Lösen (1) und (2) für x und y finden wir IX = o IX – IAV Stockfoto

RM2CEDK2T–. Eine elementare Abhandlung über die Differential-und Integralrechnung. 198 BEISPIELE. Daher ist es kein Mehrpunkt. Wenn x > oder yx Daher ist der Punkt der ersten Art, und die Tangentzur Kurve am Punkt machen mit der Achse von x Winkeln, deren Tangenten sind -f- ^/a und - Za- 2. Untersuchen Sie x* + 2ax2y - ayz = 0 für mehrere Punkte. Wir gehen nach der zweiten Methode vor, da alle kritischen Punkte in diesem Beispiel nicht leicht durch Prüfung zu finden sind. J = 4^ + «y) = 0; (1) 0 = B(A*-iy) ==; (2) dy 4#3 -f- 4:axy dx 3ay2 – 2ax2 Lösen (1) und (2) für x und y finden wir IX = o IX – IAV

$. Angewandte Kalkül; Grundsätze und Anwendungen . Die Evolvente des Kreises wird durch die Gleichungen angegeben, X = a(cos^ + 0sin0),y = A{smd – 0cos^). AP ist der Bogen einer Evolvente des Kreises. 3. Das Cycloid x = a vers^ (y/CT) ^ ^2 ay – y^. dy V2 ay – y^ (PY adx y dx^ y^ ersetzt diese Werte in (3) des Art. 94: 2/=-ft x = A = 2 V- 2ai8-i32; .-. A = avers-i (-/3/A) db V -2al3- 13^. (1) der Ort von (1) ist ein anderes Cycloid gleich dem gegebenen, die GLEICHUNG DES HÖCHSTEN Punktes EVOLUTE 147 ist am Ursprung; das heißt, die Evolution von Acycloid ist ein gleiches Cycloid. So ist die Evolution des Bogens Stockfoto$

RM2CGH242–. Angewandte Kalkül; Grundsätze und Anwendungen . Die Evolvente des Kreises wird durch die Gleichungen angegeben, X = a(cos^ + 0sin0),y = A{smd – 0cos^). AP ist der Bogen einer Evolvente des Kreises. 3. Das Cycloid x = a vers^ (y/CT) ^ ^2 ay – y^. dy V2 ay – y^ (PY adx y dx^ y^ ersetzt diese Werte in (3) des Art. 94: 2/=-ft x = A = 2 V- 2ai8-i32; .-. A = avers-i (-/3/A) db V -2al3- 13^. (1) der Ort von (1) ist ein anderes Cycloid gleich dem gegebenen, die GLEICHUNG DES HÖCHSTEN Punktes EVOLUTE 147 ist am Ursprung; das heißt, die Evolution von Acycloid ist ein gleiches Cycloid. So ist die Evolution des Bogens

$. Angewandte Kalkül; Grundsätze und Anwendungen . Die Evolvente des Kreises wird durch die Gleichungen angegeben, X = a(cos^ + 0sin0),y = A{smd – 0cos^). AP ist der Bogen einer Evolvente des Kreises. 3. Das Cycloid x = a vers^ (y/CT) ^ ^2 ay – y^. dy V2 ay – y^ (PY adx y dx^ y^ ersetzt diese Werte in (3) des Art. 94: 2/=-ft x = A = 2 V- 2ai8-i32; .-. A = avers-i (-/3/A) db V -2al3- 13^. (1) der Ort von (1) ist ein anderes Cycloid gleich dem gegebenen, die GLEICHUNG DES HÖCHSTEN Punktes EVOLUTE 147 ist am Ursprung; das heißt, die Evolution von Acycloid ist ein gleiches Cycloid. So ist die Evolution des Bogens Stockfoto$

RM2CGH2AW–. Angewandte Kalkül; Grundsätze und Anwendungen . Die Evolvente des Kreises wird durch die Gleichungen angegeben, X = a(cos^ + 0sin0),y = A{smd – 0cos^). AP ist der Bogen einer Evolvente des Kreises. 3. Das Cycloid x = a vers^ (y/CT) ^ ^2 ay – y^. dy V2 ay – y^ (PY adx y dx^ y^ ersetzt diese Werte in (3) des Art. 94: 2/=-ft x = A = 2 V- 2ai8-i32; .-. A = avers-i (-/3/A) db V -2al3- 13^. (1) der Ort von (1) ist ein anderes Cycloid gleich dem gegebenen, die GLEICHUNG DES HÖCHSTEN Punktes EVOLUTE 147 ist am Ursprung; das heißt, die Evolution von Acycloid ist ein gleiches Cycloid. So ist die Evolution des Bogens

$. Commentarii Academiae scientiarum imperialis Petropolitanae . aturam curaarum perhuiusmodi aequationes indicare, difficitas cemo-rata quidem toUeretur, at vtrum curua etfet algebraicaan tranlcendens non tam ficile appareret. Huic veroincommodo fequenti modo resteretur. §. 45. Sit arcus AMrrj- et Radius ofculi M O – rdataque fit aequatio quaecunque inter s et r. Ponan-tur APzi;jv, PMzq/ fitque dy:izpdx hisque pofitis, . , , – dx{x--pp)lerit ds – dxVipp-^i) et r – ^---^. Ex illa vero aequatione eft dx^ji-pj^zrr-» ^^ ^^^^ autera – rdp , . • ^^ 1 Zxl –^ Quamobrem proueniet haec aequa- ti Stockfoto$

RM2CDE7WE–. Commentarii Academiae scientiarum imperialis Petropolitanae . aturam curaarum perhuiusmodi aequationes indicare, difficitas cemo-rata quidem toUeretur, at vtrum curua etfet algebraicaan tranlcendens non tam ficile appareret. Huic veroincommodo fequenti modo resteretur. §. 45. Sit arcus AMrrj- et Radius ofculi M O – rdataque fit aequatio quaecunque inter s et r. Ponan-tur APzi;jv, PMzq/ fitque dy:izpdx hisque pofitis, . , , – dx{x--pp)lerit ds – dxVipp-^i) et r – ^---^. Ex illa vero aequatione eft dx^ji-pj^zrr-» ^^ ^^^^ autera – rdp , . • ^^ 1 Zxl –^ Quamobrem proueniet haec aequa- ti

. Eine elementare Abhandlung über die Differential-und Integralrechnung. Abb. 31. BEISPIELE. 20? dy 4ax dx SX2 3f cVydx* -8a2 9x* (2a - x)* Wenn x = 0 oder 2a, y = 0; .*. Die Kurve schneidet die Achse ofx am Ursprung und bei x = 2rz.um die Gleichung des Asymptoten zu finden, haben wir y ?(-#- (-£- )• also ?/ = - A? -f fa ist die Gleichung des Asymptoten, und da der nächste Begriff des Ausdrucks positiv ist, die Krümeln über dem Asymptoten. Wenn wir die erste Ableitung für x = 0, y = 0 auswerten, haben wir dy 4:ax – dx2 4a – 6x dx sy2 dy 6y dx A i£) =£ = cc> wlien *=*; fy= /2a dx 3y ± o 9, wenn y = 0 Stockfoto

RM2CEDJX2–. Eine elementare Abhandlung über die Differential-und Integralrechnung. Abb. 31. BEISPIELE. 20? dy 4ax dx SX2 3f cVydx* -8a2 9x* (2a - x)* Wenn x = 0 oder 2a, y = 0; .*. Die Kurve schneidet die Achse ofx am Ursprung und bei x = 2rz.um die Gleichung des Asymptoten zu finden, haben wir y ?(-#- (-£- )• also ?/ = - A? -f fa ist die Gleichung des Asymptoten, und da der nächste Begriff des Ausdrucks positiv ist, die Krümeln über dem Asymptoten. Wenn wir die erste Ableitung für x = 0, y = 0 auswerten, haben wir dy 4:ax – dx2 4a – 6x dx sy2 dy 6y dx A i£) =£ = cc> wlien *=*; fy= /2a dx 3y ± o 9, wenn y = 0

. Differential- und Integralrechnung. Dxdu 4 x* - 3 x2! o27 j0i7o Ty 0,0 dx 12 X2 – 6 xdx 0 dy 2dx0,0 lt* IdyV dy , . ••• Uj = •••^-±= >attheongm. Daher hat die Kurve am Ursprung (o, o) zwei Tangenten, die mit der .ar-Achse übereinstimmen. Aus der Gleichung der Kurve haben wir y = ± y/x3(i – x). Da x also nicht negativ sein kann, liegt die Kurve im ersten und vierten Quadranten und ist symmetrisch mit der #-Achse. Daher ist der Ursprung eine Spitze der ersten Art. 4. Zeigen Sie, dass das Cissoid (2 a - x)y2 = XS eine Spitze der ersten Spezies am Ursprung hat. 5. Zeigen Sie, dass (y - x2)2 Stockfoto

RM2CEPE7J–. Differential- und Integralrechnung. Dxdu 4 x* - 3 x2! o27 j0i7o Ty 0,0 dx 12 X2 – 6 xdx 0 dy 2dx0,0 lt* IdyV dy , . ••• Uj = •••^-±= >attheongm. Daher hat die Kurve am Ursprung (o, o) zwei Tangenten, die mit der .ar-Achse übereinstimmen. Aus der Gleichung der Kurve haben wir y = ± y/x3(i – x). Da x also nicht negativ sein kann, liegt die Kurve im ersten und vierten Quadranten und ist symmetrisch mit der #-Achse. Daher ist der Ursprung eine Spitze der ersten Art. 4. Zeigen Sie, dass das Cissoid (2 a - x)y2 = XS eine Spitze der ersten Spezies am Ursprung hat. 5. Zeigen Sie, dass (y - x2)2

. Die Americana : eine universelle Referenzbibliothek, bestehend aus den Künsten und Wissenschaften, Literatur, Geschichte, Biographie, Geographie, Handel, etc. Der Welt . Let w=ex(cos y+i sin y). Dann du dv – = ex cos y=-z,dx dy du dv – --e*smy--rx. Daher hat w ein Derivat und weiters dz = M/. Eine Funktion, die Single-valued througouta Region S und hat eine kontinuierliche Derivat ins wird gesagt, analytisch in S sein. Die Begriffe holo-tnorphic, monogen, und synectic sind auch einige Male in diesem Sinne verwendet. 4. Konformales Mapping. – bei zwei beliebigen Funktionen U = (x,y), V-tp(x,y), (2) können wir sie geometr interpretieren Stockfoto

RM2CH8BP6–. Die Americana : eine universelle Referenzbibliothek, bestehend aus den Künsten und Wissenschaften, Literatur, Geschichte, Biographie, Geographie, Handel, etc. Der Welt . Let w=ex(cos y+i sin y). Dann du dv – = ex cos y=-z,dx dy du dv – --e*smy--rx. Daher hat w ein Derivat und weiters dz = M/. Eine Funktion, die Single-valued througouta Region S und hat eine kontinuierliche Derivat ins wird gesagt, analytisch in S sein. Die Begriffe holo-tnorphic, monogen, und synectic sind auch einige Male in diesem Sinne verwendet. 4. Konformales Mapping. – bei zwei beliebigen Funktionen U = (x,y), V-tp(x,y), (2) können wir sie geometr interpretieren

Dy dx Stockfotos & Bilder

Dy dx Stockfotos & Bilder

Download-Bestätigung

Passwortbestätigung

Suchergebnisse für Dy dx Stock-Fotos & Bilder (157)

Nach Kollektionen der Agentur filtern

Suchmanager

Erhalten Sie großartige Funktionen mit Ihrem kostenlosen Konto

Lass dich für dein nächstes Projekt inspirieren!