Schnellfilter:
Kartesischen koordinaten Stockfotos & Bilder
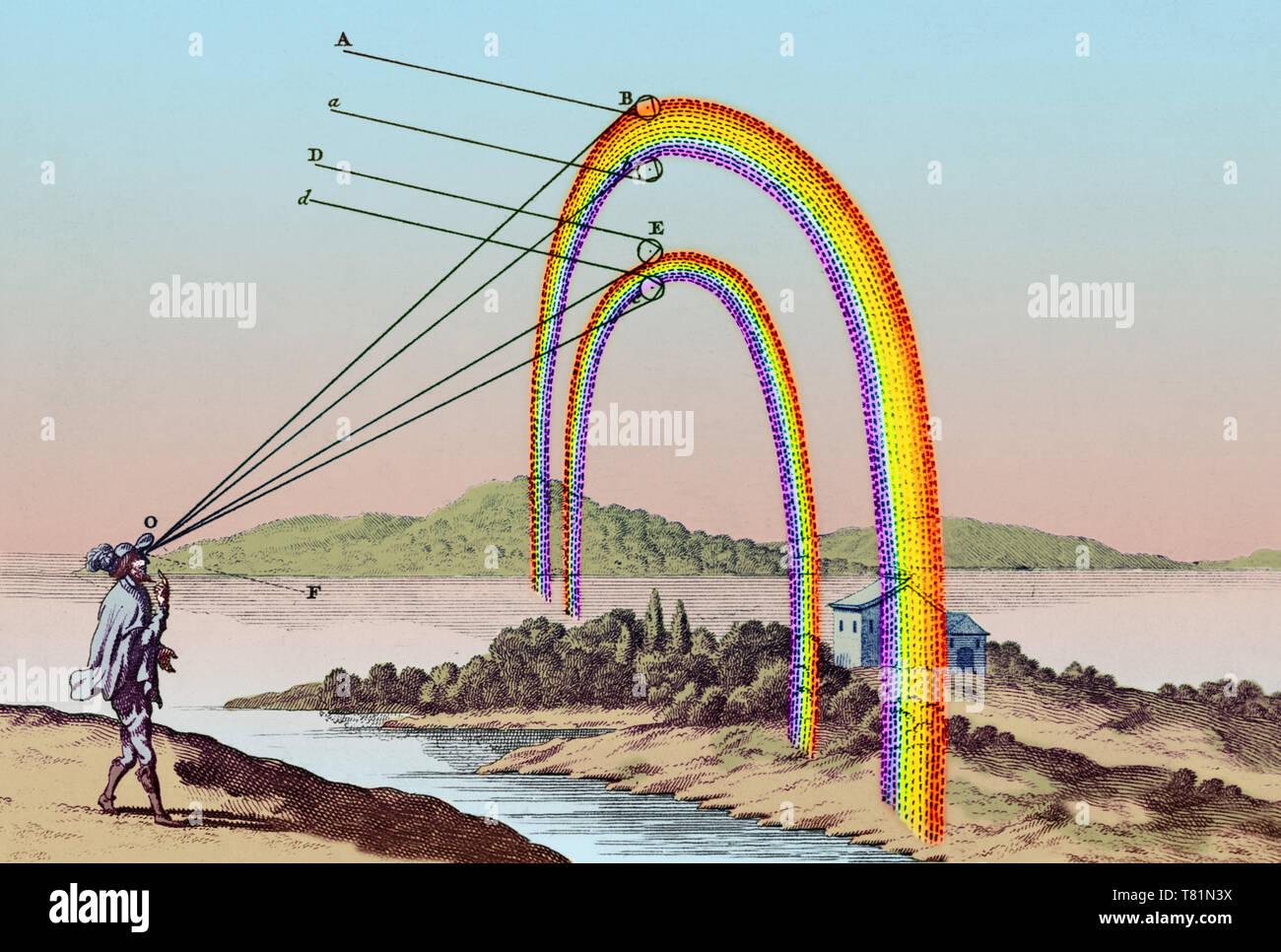 © René Descartes, doppelten Regenbogen, 1637 Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/ren-descartes-doppelten-regenbogen-1637-image245900926.html
© René Descartes, doppelten Regenbogen, 1637 Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/ren-descartes-doppelten-regenbogen-1637-image245900926.htmlRMT81N3X–© René Descartes, doppelten Regenbogen, 1637
 Vektordarstellung kartesischer Koordinaten Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektordarstellung-kartesischer-koordinaten-image571427575.html
Vektordarstellung kartesischer Koordinaten Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektordarstellung-kartesischer-koordinaten-image571427575.htmlRF2T5JNKK–Vektordarstellung kartesischer Koordinaten
 Kartesische und polare Koordinaten Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesische-und-polare-koordinaten-25485627.html
Kartesische und polare Koordinaten Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesische-und-polare-koordinaten-25485627.htmlRMBDCY4Y–Kartesische und polare Koordinaten
 XYZ - Metall drei letzte Buchstaben des Alphabets (oder kartesischen Koordinatensystem) in Vintage Buchdruck-Typ Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-xyz-metall-drei-letzte-buchstaben-des-alphabets-oder-kartesischen-koordinatensystem-in-vintage-buchdruck-typ-43658472.html
XYZ - Metall drei letzte Buchstaben des Alphabets (oder kartesischen Koordinatensystem) in Vintage Buchdruck-Typ Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-xyz-metall-drei-letzte-buchstaben-des-alphabets-oder-kartesischen-koordinatensystem-in-vintage-buchdruck-typ-43658472.htmlRFCF0PR4–XYZ - Metall drei letzte Buchstaben des Alphabets (oder kartesischen Koordinatensystem) in Vintage Buchdruck-Typ
 Warme und kalte Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-warme-und-kalte-89236749.html
Warme und kalte Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-warme-und-kalte-89236749.htmlRFF552AN–Warme und kalte
 Das polare Koordinatensystem Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/das-polare-koordinatensystem-image543771511.html
Das polare Koordinatensystem Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/das-polare-koordinatensystem-image543771511.htmlRM2PGJX33–Das polare Koordinatensystem
 kartesische Ebene, Graph einer Gleichung auf x=2. Illustration isoliert auf weißem Hintergrund Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesische-ebene-graph-einer-gleichung-auf-x=2-illustration-isoliert-auf-weissem-hintergrund-image461131267.html
kartesische Ebene, Graph einer Gleichung auf x=2. Illustration isoliert auf weißem Hintergrund Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesische-ebene-graph-einer-gleichung-auf-x=2-illustration-isoliert-auf-weissem-hintergrund-image461131267.htmlRF2HP69HR–kartesische Ebene, Graph einer Gleichung auf x=2. Illustration isoliert auf weißem Hintergrund
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Vorlage für mathematischen Maßstab. Vektordarstellung isoliert auf weißem Hintergrund Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-vorlage-fur-mathematischen-massstab-vektordarstellung-isoliert-auf-weissem-hintergrund-image515236864.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Vorlage für mathematischen Maßstab. Vektordarstellung isoliert auf weißem Hintergrund Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-vorlage-fur-mathematischen-massstab-vektordarstellung-isoliert-auf-weissem-hintergrund-image515236864.htmlRF2MX71TG–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Vorlage für mathematischen Maßstab. Vektordarstellung isoliert auf weißem Hintergrund
 Wissenschaftlicher Taschenrechner mit trigonometrischen, exponentiell, Koordinaten-Umwandlung (kartesischen / polar) und andere Tasten sichtbar. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-wissenschaftlicher-taschenrechner-mit-trigonometrischen-exponentiell-koordinaten-umwandlung-kartesischen-polar-und-andere-tasten-sichtbar-79870600.html
Wissenschaftlicher Taschenrechner mit trigonometrischen, exponentiell, Koordinaten-Umwandlung (kartesischen / polar) und andere Tasten sichtbar. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-wissenschaftlicher-taschenrechner-mit-trigonometrischen-exponentiell-koordinaten-umwandlung-kartesischen-polar-und-andere-tasten-sichtbar-79870600.htmlRFEHXBNC–Wissenschaftlicher Taschenrechner mit trigonometrischen, exponentiell, Koordinaten-Umwandlung (kartesischen / polar) und andere Tasten sichtbar.
 Energie-Kurve Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-energie-kurve-101056546.html
Energie-Kurve Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-energie-kurve-101056546.htmlRMFTBEJA–Energie-Kurve
 Die Punkte in der Koordinatenebene in der Mathematik. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-mathematische-ressourcen-fur-lehrer-und-schuler-image558030349.html
Die Punkte in der Koordinatenebene in der Mathematik. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-mathematische-ressourcen-fur-lehrer-und-schuler-image558030349.htmlRF2RBTDB9–Die Punkte in der Koordinatenebene in der Mathematik. Mathematische Ressourcen für Lehrer und Schüler.
 Kindermodelle "kalt Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kindermodelle-kalt-101056551.html
Kindermodelle "kalt Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kindermodelle-kalt-101056551.htmlRMFTBEJF–Kindermodelle "kalt
 Kartesischen Koordinatensystem Bauplan Flugzeug Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesischen-koordinatensystem-bauplan-flugzeug-75364175.html
Kartesischen Koordinatensystem Bauplan Flugzeug Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesischen-koordinatensystem-bauplan-flugzeug-75364175.htmlRFEAH3NK–Kartesischen Koordinatensystem Bauplan Flugzeug
 Kartesisches Koordinatensystem in zwei Dimensionen mit Quadranten. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-in-zwei-dimensionen-mit-quadranten-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-image470631827.html
Kartesisches Koordinatensystem in zwei Dimensionen mit Quadranten. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-in-zwei-dimensionen-mit-quadranten-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-image470631827.htmlRF2J9K3KF–Kartesisches Koordinatensystem in zwei Dimensionen mit Quadranten. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y
 Analytische Mechanik für Studierende der Physik und Ingenieurwissenschaften. ody jeder Form und Distributionof Messe - Die illustrative Beispiele der letzten pagesare durch spezielle Methoden gearbeitet, um Zinn - Tatsache, dass in einer großen Zahl von Problemen die Leichtigkeit, mit dem Mitte der Masse ermittelt werden können, hängt ab vom thechoice des Elements von Masse zu bringen. Die folgenden Allgemeinen ex-Druck für ein Element der Masse verwendet werden, was theshape des Körpers oder die Verteilung der Masse: (a) Wenn die begrenzende Flächen der Karosserie sind givenin die kartesischen Koordinaten der Masse eines infinitesimalc Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/analytische-mechanik-fur-studierende-der-physik-und-ingenieurwissenschaften-ody-jeder-form-und-distributionof-messe-die-illustrative-beispiele-der-letzten-pagesare-durch-spezielle-methoden-gearbeitet-um-zinn-tatsache-dass-in-einer-grossen-zahl-von-problemen-die-leichtigkeit-mit-dem-mitte-der-masse-ermittelt-werden-konnen-hangt-ab-vom-thechoice-des-elements-von-masse-zu-bringen-die-folgenden-allgemeinen-ex-druck-fur-ein-element-der-masse-verwendet-werden-was-theshape-des-korpers-oder-die-verteilung-der-masse-a-wenn-die-begrenzende-flachen-der-karosserie-sind-givenin-die-kartesischen-koordinaten-der-masse-eines-infinitesimalc-image339023900.html
Analytische Mechanik für Studierende der Physik und Ingenieurwissenschaften. ody jeder Form und Distributionof Messe - Die illustrative Beispiele der letzten pagesare durch spezielle Methoden gearbeitet, um Zinn - Tatsache, dass in einer großen Zahl von Problemen die Leichtigkeit, mit dem Mitte der Masse ermittelt werden können, hängt ab vom thechoice des Elements von Masse zu bringen. Die folgenden Allgemeinen ex-Druck für ein Element der Masse verwendet werden, was theshape des Körpers oder die Verteilung der Masse: (a) Wenn die begrenzende Flächen der Karosserie sind givenin die kartesischen Koordinaten der Masse eines infinitesimalc Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/analytische-mechanik-fur-studierende-der-physik-und-ingenieurwissenschaften-ody-jeder-form-und-distributionof-messe-die-illustrative-beispiele-der-letzten-pagesare-durch-spezielle-methoden-gearbeitet-um-zinn-tatsache-dass-in-einer-grossen-zahl-von-problemen-die-leichtigkeit-mit-dem-mitte-der-masse-ermittelt-werden-konnen-hangt-ab-vom-thechoice-des-elements-von-masse-zu-bringen-die-folgenden-allgemeinen-ex-druck-fur-ein-element-der-masse-verwendet-werden-was-theshape-des-korpers-oder-die-verteilung-der-masse-a-wenn-die-begrenzende-flachen-der-karosserie-sind-givenin-die-kartesischen-koordinaten-der-masse-eines-infinitesimalc-image339023900.htmlRM2AKFTCC–Analytische Mechanik für Studierende der Physik und Ingenieurwissenschaften. ody jeder Form und Distributionof Messe - Die illustrative Beispiele der letzten pagesare durch spezielle Methoden gearbeitet, um Zinn - Tatsache, dass in einer großen Zahl von Problemen die Leichtigkeit, mit dem Mitte der Masse ermittelt werden können, hängt ab vom thechoice des Elements von Masse zu bringen. Die folgenden Allgemeinen ex-Druck für ein Element der Masse verwendet werden, was theshape des Körpers oder die Verteilung der Masse: (a) Wenn die begrenzende Flächen der Karosserie sind givenin die kartesischen Koordinaten der Masse eines infinitesimalc
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image603618073.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image603618073.htmlRF2X21509–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung
 Es wird ein xy-Raster/Diagramm mit Rasterlinien angezeigt. Es handelt sich um das kartesische Koordinatensystem mit beiden beschrifteten Achsen, Vintage-Linien-Zeichnung oder Gravur Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/es-wird-ein-xy-rasterdiagramm-mit-rasterlinien-angezeigt-es-handelt-sich-um-das-kartesische-koordinatensystem-mit-beiden-beschrifteten-achsen-vintage-linien-zeichnung-oder-gravur-image348663823.html
Es wird ein xy-Raster/Diagramm mit Rasterlinien angezeigt. Es handelt sich um das kartesische Koordinatensystem mit beiden beschrifteten Achsen, Vintage-Linien-Zeichnung oder Gravur Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/es-wird-ein-xy-rasterdiagramm-mit-rasterlinien-angezeigt-es-handelt-sich-um-das-kartesische-koordinatensystem-mit-beiden-beschrifteten-achsen-vintage-linien-zeichnung-oder-gravur-image348663823.htmlRF2B7707B–Es wird ein xy-Raster/Diagramm mit Rasterlinien angezeigt. Es handelt sich um das kartesische Koordinatensystem mit beiden beschrifteten Achsen, Vintage-Linien-Zeichnung oder Gravur
 Achsen der mit Hilfe von leinsamen dargestellt Koordinaten. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-achsen-der-mit-hilfe-von-leinsamen-dargestellt-koordinaten-310970205.html
Achsen der mit Hilfe von leinsamen dargestellt Koordinaten. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-achsen-der-mit-hilfe-von-leinsamen-dargestellt-koordinaten-310970205.htmlRFS1WWJN–Achsen der mit Hilfe von leinsamen dargestellt Koordinaten.
 Kartesisches Koordinatensystem editierbare Symbol design Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-editierbare-symbol-design-image332385500.html
Kartesisches Koordinatensystem editierbare Symbol design Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-editierbare-symbol-design-image332385500.htmlRF2A8ND2M–Kartesisches Koordinatensystem editierbare Symbol design
 Der Regenbogen, gezeichnet nach kartesischen Physik. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-der-regenbogen-gezeichnet-nach-kartesischen-physik-103985272.html
Der Regenbogen, gezeichnet nach kartesischen Physik. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-der-regenbogen-gezeichnet-nach-kartesischen-physik-103985272.htmlRMG14X7M–Der Regenbogen, gezeichnet nach kartesischen Physik.
 Vektordarstellung von kugelförmigen Koordinaten Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektordarstellung-von-kugelformigen-koordinaten-image571427641.html
Vektordarstellung von kugelförmigen Koordinaten Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektordarstellung-von-kugelformigen-koordinaten-image571427641.htmlRF2T5JNP1–Vektordarstellung von kugelförmigen Koordinaten
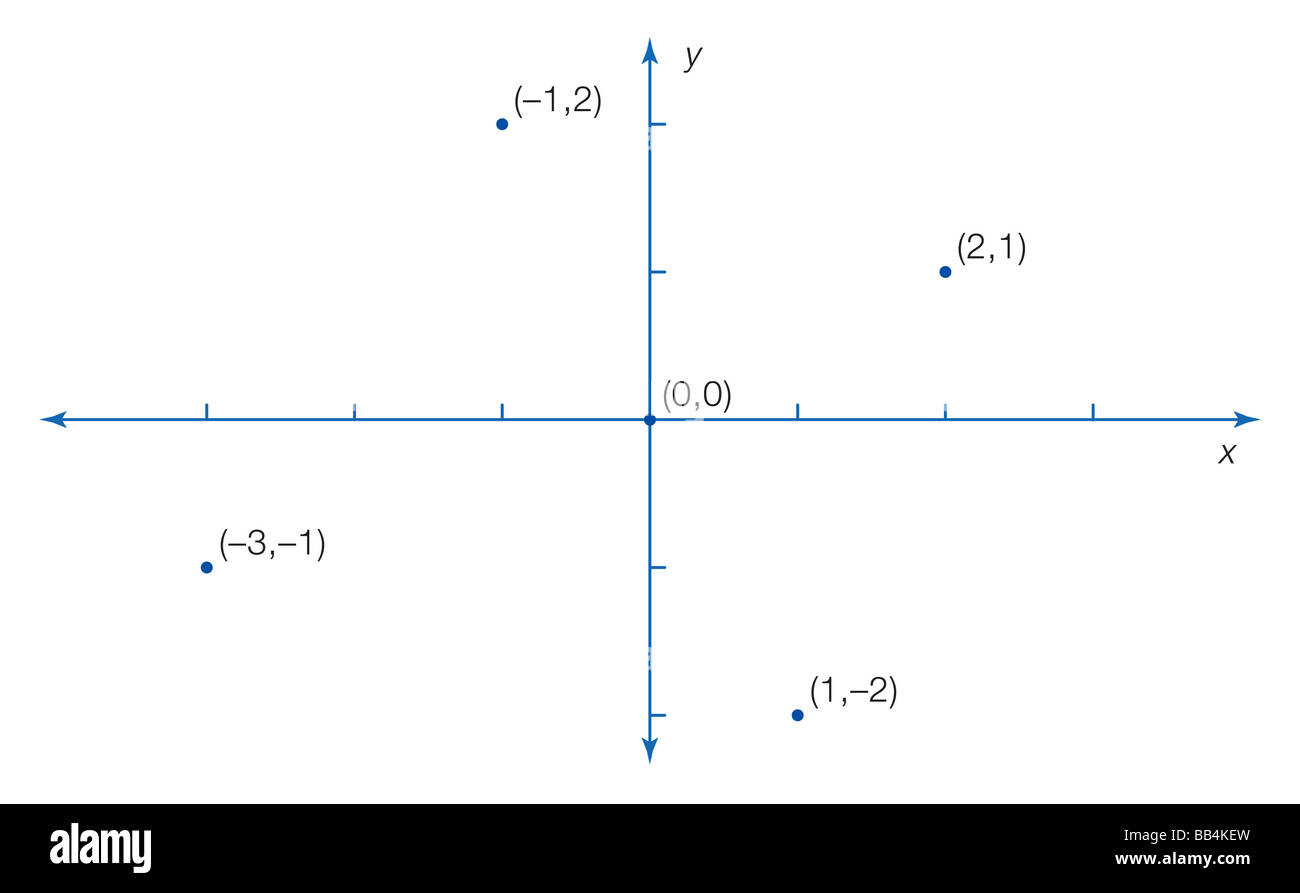 Einige Punkte sind in einem zweidimensionalen Diagramm, bekannt als die kartesischen Ebene gekennzeichnet. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-einige-punkte-sind-in-einem-zweidimensionalen-diagramm-bekannt-als-die-kartesischen-ebene-gekennzeichnet-24074705.html
Einige Punkte sind in einem zweidimensionalen Diagramm, bekannt als die kartesischen Ebene gekennzeichnet. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-einige-punkte-sind-in-einem-zweidimensionalen-diagramm-bekannt-als-die-kartesischen-ebene-gekennzeichnet-24074705.htmlRMBB4KEW–Einige Punkte sind in einem zweidimensionalen Diagramm, bekannt als die kartesischen Ebene gekennzeichnet.
 Ein rechteckiges Koordinatensystem im Raum. Abbildung der Punktkoordinaten Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/ein-rechteckiges-koordinatensystem-im-raum-abbildung-der-punktkoordinaten-image594768271.html
Ein rechteckiges Koordinatensystem im Raum. Abbildung der Punktkoordinaten Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/ein-rechteckiges-koordinatensystem-im-raum-abbildung-der-punktkoordinaten-image594768271.htmlRF2WFJ0YY–Ein rechteckiges Koordinatensystem im Raum. Abbildung der Punktkoordinaten
 Kartesisches Koordinatensystem Symbol auf weißem Hintergrund. Einfaches element Abbildung von Bildung Konzept. kartesischen Koordinatensystem Symbol desi Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-symbol-auf-weissem-hintergrund-einfaches-element-abbildung-von-bildung-konzept-kartesischen-koordinatensystem-symbol-desi-image336378371.html
Kartesisches Koordinatensystem Symbol auf weißem Hintergrund. Einfaches element Abbildung von Bildung Konzept. kartesischen Koordinatensystem Symbol desi Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-symbol-auf-weissem-hintergrund-einfaches-element-abbildung-von-bildung-konzept-kartesischen-koordinatensystem-symbol-desi-image336378371.htmlRF2AF7A17–Kartesisches Koordinatensystem Symbol auf weißem Hintergrund. Einfaches element Abbildung von Bildung Konzept. kartesischen Koordinatensystem Symbol desi
 Kartesisches Koordinatensystem Umriss Vektor-Symbol. Dünne Linie schwarz kartesischen Koordinatensystem Symbol, flache Vektor einfache Element Illustration aus editab Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-umriss-vektor-symbol-dunne-linie-schwarz-kartesischen-koordinatensystem-symbol-flache-vektor-einfache-element-illustration-aus-editab-image397506861.html
Kartesisches Koordinatensystem Umriss Vektor-Symbol. Dünne Linie schwarz kartesischen Koordinatensystem Symbol, flache Vektor einfache Element Illustration aus editab Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-umriss-vektor-symbol-dunne-linie-schwarz-kartesischen-koordinatensystem-symbol-flache-vektor-einfache-element-illustration-aus-editab-image397506861.htmlRF2E2M01H–Kartesisches Koordinatensystem Umriss Vektor-Symbol. Dünne Linie schwarz kartesischen Koordinatensystem Symbol, flache Vektor einfache Element Illustration aus editab
 Formen in der kartesischen Ebene. Grafik eines Rechtecks im dritten Quadranten der Koordinatenebene haben sowohl die x- als auch die y-Achse negative Werte Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/formen-in-der-kartesischen-ebene-grafik-eines-rechtecks-im-dritten-quadranten-der-koordinatenebene-haben-sowohl-die-x-als-auch-die-y-achse-negative-werte-image461131420.html
Formen in der kartesischen Ebene. Grafik eines Rechtecks im dritten Quadranten der Koordinatenebene haben sowohl die x- als auch die y-Achse negative Werte Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/formen-in-der-kartesischen-ebene-grafik-eines-rechtecks-im-dritten-quadranten-der-koordinatenebene-haben-sowohl-die-x-als-auch-die-y-achse-negative-werte-image461131420.htmlRF2HP69R8–Formen in der kartesischen Ebene. Grafik eines Rechtecks im dritten Quadranten der Koordinatenebene haben sowohl die x- als auch die y-Achse negative Werte
 Süße Geometrie. Sommer-Hausaufgaben. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-susse-geometrie-sommer-hausaufgaben-89236989.html
Süße Geometrie. Sommer-Hausaufgaben. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-susse-geometrie-sommer-hausaufgaben-89236989.htmlRFF552K9–Süße Geometrie. Sommer-Hausaufgaben.
 Wissenschaftlicher Taschenrechner mit trigonometrischen, exponentielle, hyperbolische und andere Tasten sichtbar. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-wissenschaftlicher-taschenrechner-mit-trigonometrischen-exponentielle-hyperbolische-und-andere-tasten-sichtbar-79884771.html
Wissenschaftlicher Taschenrechner mit trigonometrischen, exponentielle, hyperbolische und andere Tasten sichtbar. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-wissenschaftlicher-taschenrechner-mit-trigonometrischen-exponentielle-hyperbolische-und-andere-tasten-sichtbar-79884771.htmlRFEHY1RF–Wissenschaftlicher Taschenrechner mit trigonometrischen, exponentielle, hyperbolische und andere Tasten sichtbar.
 Ein Jungle Gym in einer Reistrocknungsanlage in Los Banos, Laguna, ermöglicht es den Kindern von Reisfarmern, die Spielplätze zu nutzen und körperliche Kraft zu entwickeln. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/ein-jungle-gym-in-einer-reistrocknungsanlage-in-los-banos-laguna-ermoglicht-es-den-kindern-von-reisfarmern-die-spielplatze-zu-nutzen-und-korperliche-kraft-zu-entwickeln-image345251865.html
Ein Jungle Gym in einer Reistrocknungsanlage in Los Banos, Laguna, ermöglicht es den Kindern von Reisfarmern, die Spielplätze zu nutzen und körperliche Kraft zu entwickeln. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/ein-jungle-gym-in-einer-reistrocknungsanlage-in-los-banos-laguna-ermoglicht-es-den-kindern-von-reisfarmern-die-spielplatze-zu-nutzen-und-korperliche-kraft-zu-entwickeln-image345251865.htmlRF2B1KG7N–Ein Jungle Gym in einer Reistrocknungsanlage in Los Banos, Laguna, ermöglicht es den Kindern von Reisfarmern, die Spielplätze zu nutzen und körperliche Kraft zu entwickeln.
 Die Punkte in der Koordinatenebene in der Mathematik. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-image558689959.html
Die Punkte in der Koordinatenebene in der Mathematik. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-image558689959.htmlRF2RCXEMR–Die Punkte in der Koordinatenebene in der Mathematik.
 Zeitdiagramm positionieren Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/zeitdiagramm-positionieren-image598526050.html
Zeitdiagramm positionieren Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/zeitdiagramm-positionieren-image598526050.htmlRF2WNN62A–Zeitdiagramm positionieren
 Kartesischen Koordinatensystem Bauplan Flugzeug Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesischen-koordinatensystem-bauplan-flugzeug-75363471.html
Kartesischen Koordinatensystem Bauplan Flugzeug Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesischen-koordinatensystem-bauplan-flugzeug-75363471.htmlRFEAH2TF–Kartesischen Koordinatensystem Bauplan Flugzeug
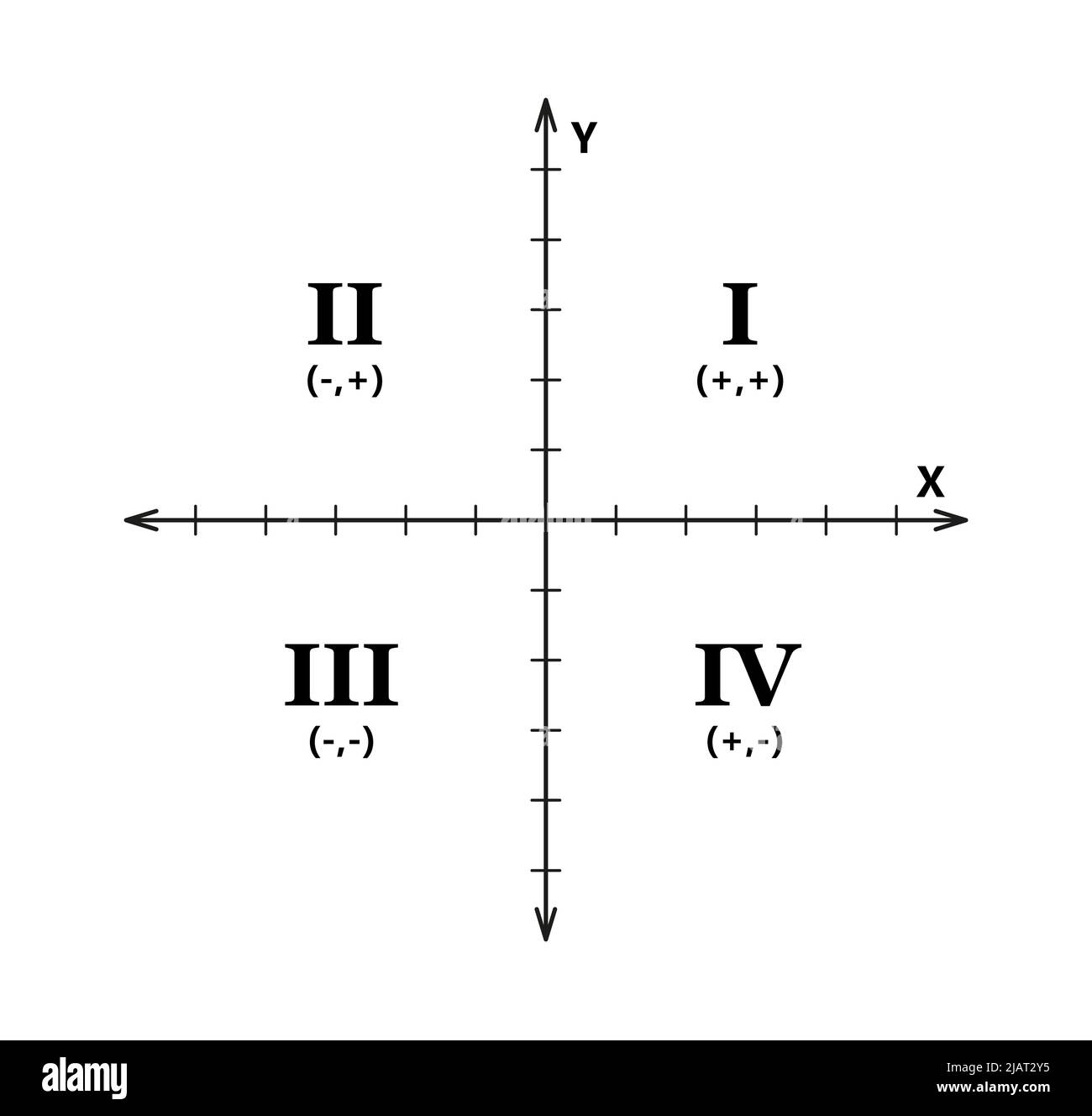 Kartesisches Koordinatensystem in zwei Dimensionen mit Quadranten. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-in-zwei-dimensionen-mit-quadranten-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-image471355673.html
Kartesisches Koordinatensystem in zwei Dimensionen mit Quadranten. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-in-zwei-dimensionen-mit-quadranten-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-image471355673.htmlRF2JAT2Y5–Kartesisches Koordinatensystem in zwei Dimensionen mit Quadranten. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y
 London, Edinburgh und Dublin Philosophische Zeitschrift und Zeitschrift für Wissenschaft . Ejr. 2.. Nehmen wir f=?4cosi^ 9 = steigend, so dass wir eine konforme Transformation haben, wenn f, V be regardedas kartesische Koordinaten in einer anderen Ebene, die Parabel Vans-Eorming in f =7r und das Latus-rectum in £2 = V2. Thecorrespondence ist in den Abbildungen dargestellt. 1 und 2, bei denen die Korrespondenten ähnlich beschriftete Punkte haben. Grad Seit mi<^ m die Bedingungen, die um % erfüllt werden sollen, werden, unter Bezugnahme auf tofig- 2, P+g = -"(f+r), ... (3) über dem Bereich LSL,,x=0 auf £=*, dx/0P=dr3,; auf fand dx/o?= -ox/9; ein ?=-?/. 32 Herr J. Proud M. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/london-edinburgh-und-dublin-philosophische-zeitschrift-und-zeitschrift-fur-wissenschaft-ejr-2-nehmen-wir-f=4cosi-9-=-steigend-so-dass-wir-eine-konforme-transformation-haben-wenn-f-v-be-regardedas-kartesische-koordinaten-in-einer-anderen-ebene-die-parabel-vans-eorming-in-f-=7r-und-das-latus-rectum-in-2-=-v2-thecorrespondence-ist-in-den-abbildungen-dargestellt-1-und-2-bei-denen-die-korrespondenten-ahnlich-beschriftete-punkte-haben-grad-seit-milt-m-die-bedingungen-die-um-erfullt-werden-sollen-werden-unter-bezugnahme-auf-tofig-2-pg-=-fr-3-uber-dem-bereich-lslx=0-auf-=-dx0p=dr3-auf-fand-dxo=-ox9-ein-=-32-herr-j-proud-m-image342757175.html
London, Edinburgh und Dublin Philosophische Zeitschrift und Zeitschrift für Wissenschaft . Ejr. 2.. Nehmen wir f=?4cosi^ 9 = steigend, so dass wir eine konforme Transformation haben, wenn f, V be regardedas kartesische Koordinaten in einer anderen Ebene, die Parabel Vans-Eorming in f =7r und das Latus-rectum in £2 = V2. Thecorrespondence ist in den Abbildungen dargestellt. 1 und 2, bei denen die Korrespondenten ähnlich beschriftete Punkte haben. Grad Seit mi<^ m die Bedingungen, die um % erfüllt werden sollen, werden, unter Bezugnahme auf tofig- 2, P+g = -"(f+r), ... (3) über dem Bereich LSL,,x=0 auf £=*, dx/0P=dr3,; auf fand dx/o?= -ox/9; ein ?=-?/. 32 Herr J. Proud M. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/london-edinburgh-und-dublin-philosophische-zeitschrift-und-zeitschrift-fur-wissenschaft-ejr-2-nehmen-wir-f=4cosi-9-=-steigend-so-dass-wir-eine-konforme-transformation-haben-wenn-f-v-be-regardedas-kartesische-koordinaten-in-einer-anderen-ebene-die-parabel-vans-eorming-in-f-=7r-und-das-latus-rectum-in-2-=-v2-thecorrespondence-ist-in-den-abbildungen-dargestellt-1-und-2-bei-denen-die-korrespondenten-ahnlich-beschriftete-punkte-haben-grad-seit-milt-m-die-bedingungen-die-um-erfullt-werden-sollen-werden-unter-bezugnahme-auf-tofig-2-pg-=-fr-3-uber-dem-bereich-lslx=0-auf-=-dx0p=dr3-auf-fand-dxo=-ox9-ein-=-32-herr-j-proud-m-image342757175.htmlRM2AWHX7K–London, Edinburgh und Dublin Philosophische Zeitschrift und Zeitschrift für Wissenschaft . Ejr. 2.. Nehmen wir f=?4cosi^ 9 = steigend, so dass wir eine konforme Transformation haben, wenn f, V be regardedas kartesische Koordinaten in einer anderen Ebene, die Parabel Vans-Eorming in f =7r und das Latus-rectum in £2 = V2. Thecorrespondence ist in den Abbildungen dargestellt. 1 und 2, bei denen die Korrespondenten ähnlich beschriftete Punkte haben. Grad Seit mi<^ m die Bedingungen, die um % erfüllt werden sollen, werden, unter Bezugnahme auf tofig- 2, P+g = -"(f+r), ... (3) über dem Bereich LSL,,x=0 auf £=*, dx/0P=dr3,; auf fand dx/o?= -ox/9; ein ?=-?/. 32 Herr J. Proud M.
 Gepunktete Dreiecke Sinus Welle. Dreieck weg. Kann für Infografiken verwendet werden. Geometrische Clean Design Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/gepunktete-dreiecke-sinus-welle-dreieck-weg-kann-fur-infografiken-verwendet-werden-geometrische-clean-design-image230253807.html
Gepunktete Dreiecke Sinus Welle. Dreieck weg. Kann für Infografiken verwendet werden. Geometrische Clean Design Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/gepunktete-dreiecke-sinus-welle-dreieck-weg-kann-fur-infografiken-verwendet-werden-geometrische-clean-design-image230253807.htmlRFRAGY27–Gepunktete Dreiecke Sinus Welle. Dreieck weg. Kann für Infografiken verwendet werden. Geometrische Clean Design
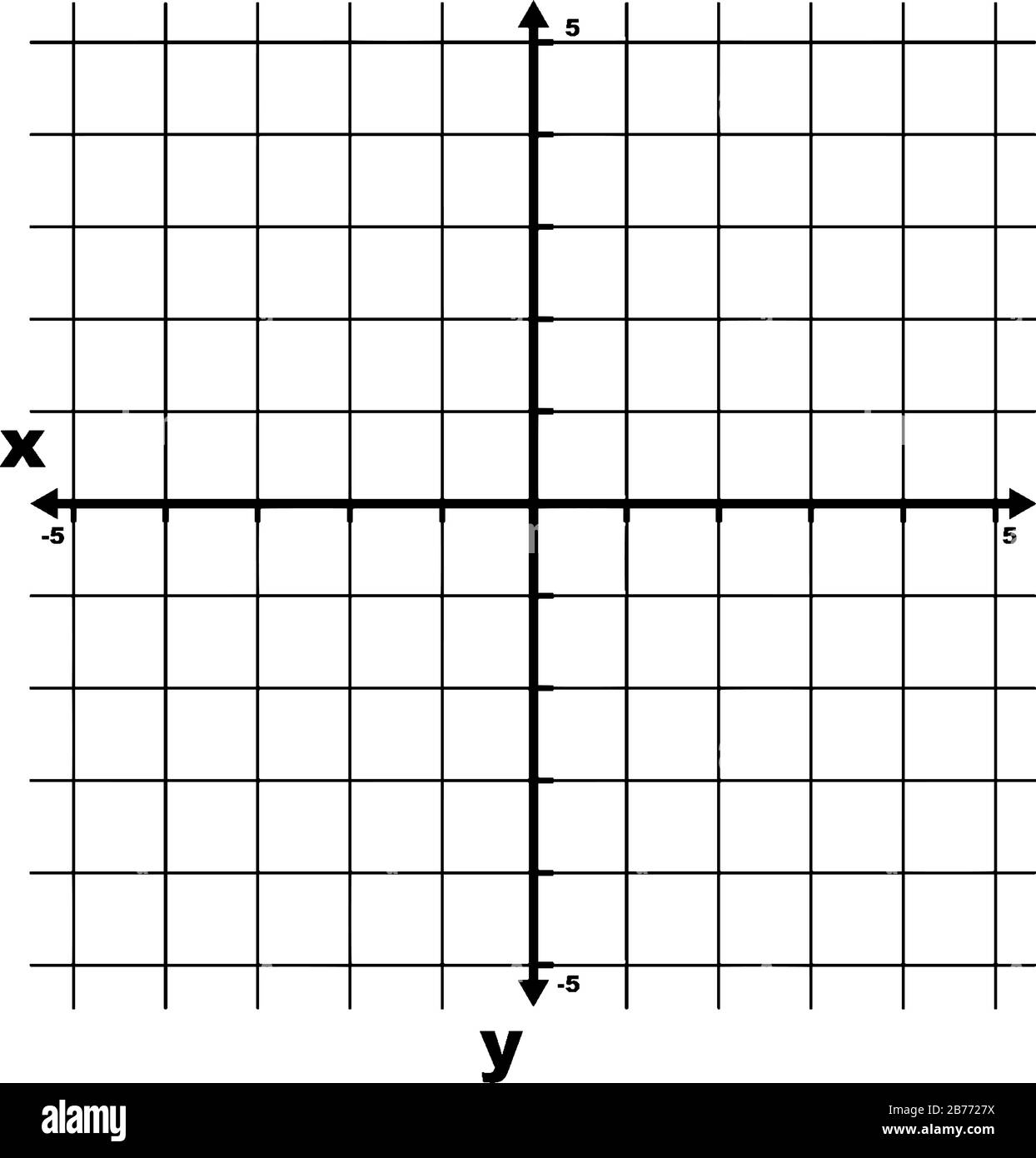 Es wird ein xy-Raster/Diagramm mit Rasterlinien angezeigt. Es ist das kartesische Koordinatensystem mit den Achsen und einigen Schritten von -5 bis 5 beschriftet, alter lin Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/es-wird-ein-xy-rasterdiagramm-mit-rasterlinien-angezeigt-es-ist-das-kartesische-koordinatensystem-mit-den-achsen-und-einigen-schritten-von-5-bis-5-beschriftet-alter-lin-image348665406.html
Es wird ein xy-Raster/Diagramm mit Rasterlinien angezeigt. Es ist das kartesische Koordinatensystem mit den Achsen und einigen Schritten von -5 bis 5 beschriftet, alter lin Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/es-wird-ein-xy-rasterdiagramm-mit-rasterlinien-angezeigt-es-ist-das-kartesische-koordinatensystem-mit-den-achsen-und-einigen-schritten-von-5-bis-5-beschriftet-alter-lin-image348665406.htmlRF2B7727X–Es wird ein xy-Raster/Diagramm mit Rasterlinien angezeigt. Es ist das kartesische Koordinatensystem mit den Achsen und einigen Schritten von -5 bis 5 beschriftet, alter lin
RFR1PN5M–Gauss'schen Funktion vektor Icon auf transparentem Hintergrund isoliert, Gauss'schen Funktion Transparenz logo Konzept
 Auf die weiße Fläche, eine Koordinatenachse geplottet mit Leinsamen. Eine aufsteigende Diagramm ist aus Süßigkeiten. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-auf-die-weisse-flache-eine-koordinatenachse-geplottet-mit-leinsamen-eine-aufsteigende-diagramm-ist-aus-sussigkeiten-310970209.html
Auf die weiße Fläche, eine Koordinatenachse geplottet mit Leinsamen. Eine aufsteigende Diagramm ist aus Süßigkeiten. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-auf-die-weisse-flache-eine-koordinatenachse-geplottet-mit-leinsamen-eine-aufsteigende-diagramm-ist-aus-sussigkeiten-310970209.htmlRFS1WWJW–Auf die weiße Fläche, eine Koordinatenachse geplottet mit Leinsamen. Eine aufsteigende Diagramm ist aus Süßigkeiten.
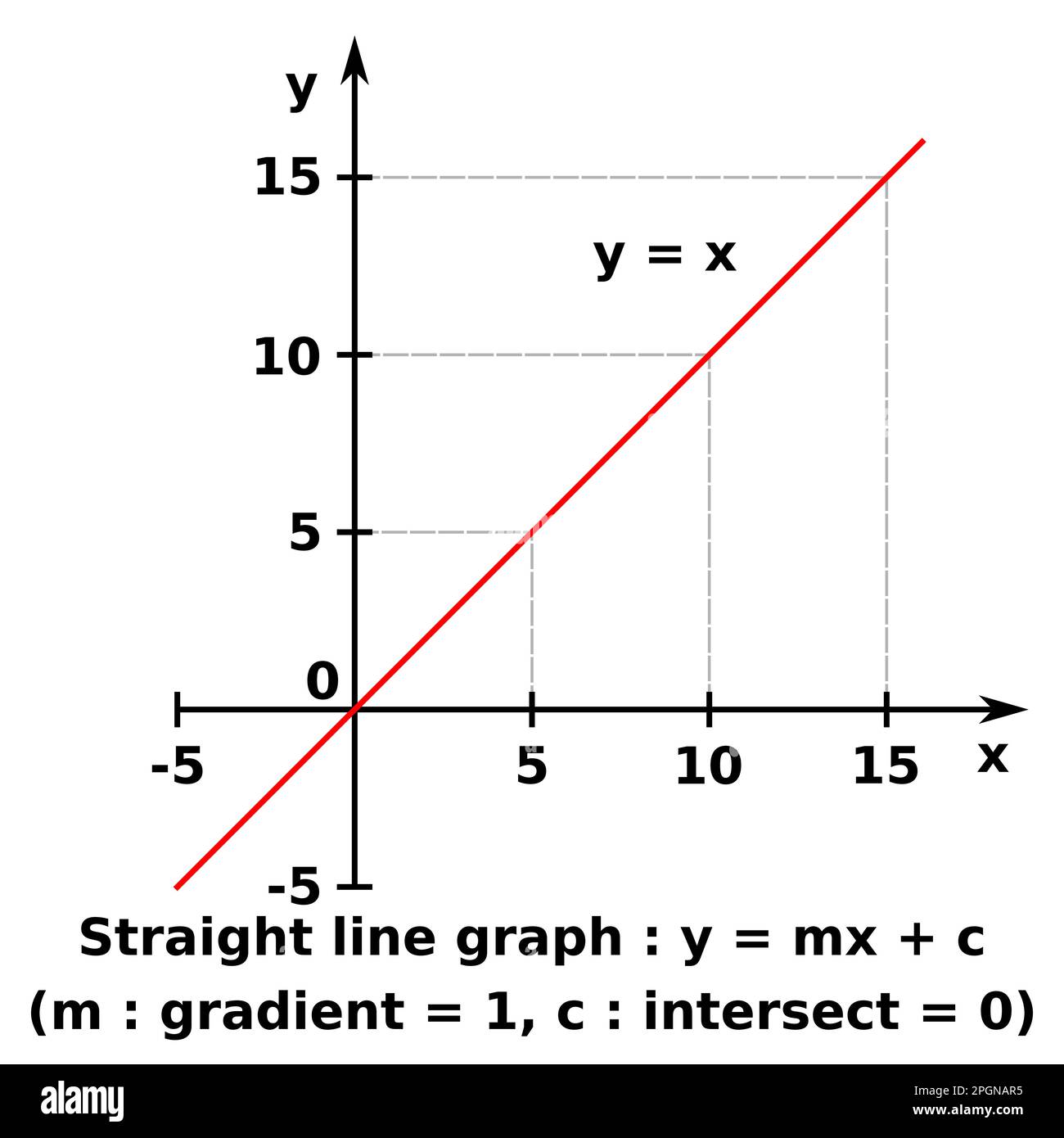 Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = x Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektorgrafik-eines-diagramms-von-x-gegen-y-einer-linearen-funktion-die-dargestellte-formel-ist-y-=-x-image543825385.html
Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = x Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektorgrafik-eines-diagramms-von-x-gegen-y-einer-linearen-funktion-die-dargestellte-formel-ist-y-=-x-image543825385.htmlRF2PGNAR5–Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = x
 Vektordarstellung zylindrischer Koordinaten Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektordarstellung-zylindrischer-koordinaten-image571427634.html
Vektordarstellung zylindrischer Koordinaten Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektordarstellung-zylindrischer-koordinaten-image571427634.htmlRF2T5JNNP–Vektordarstellung zylindrischer Koordinaten
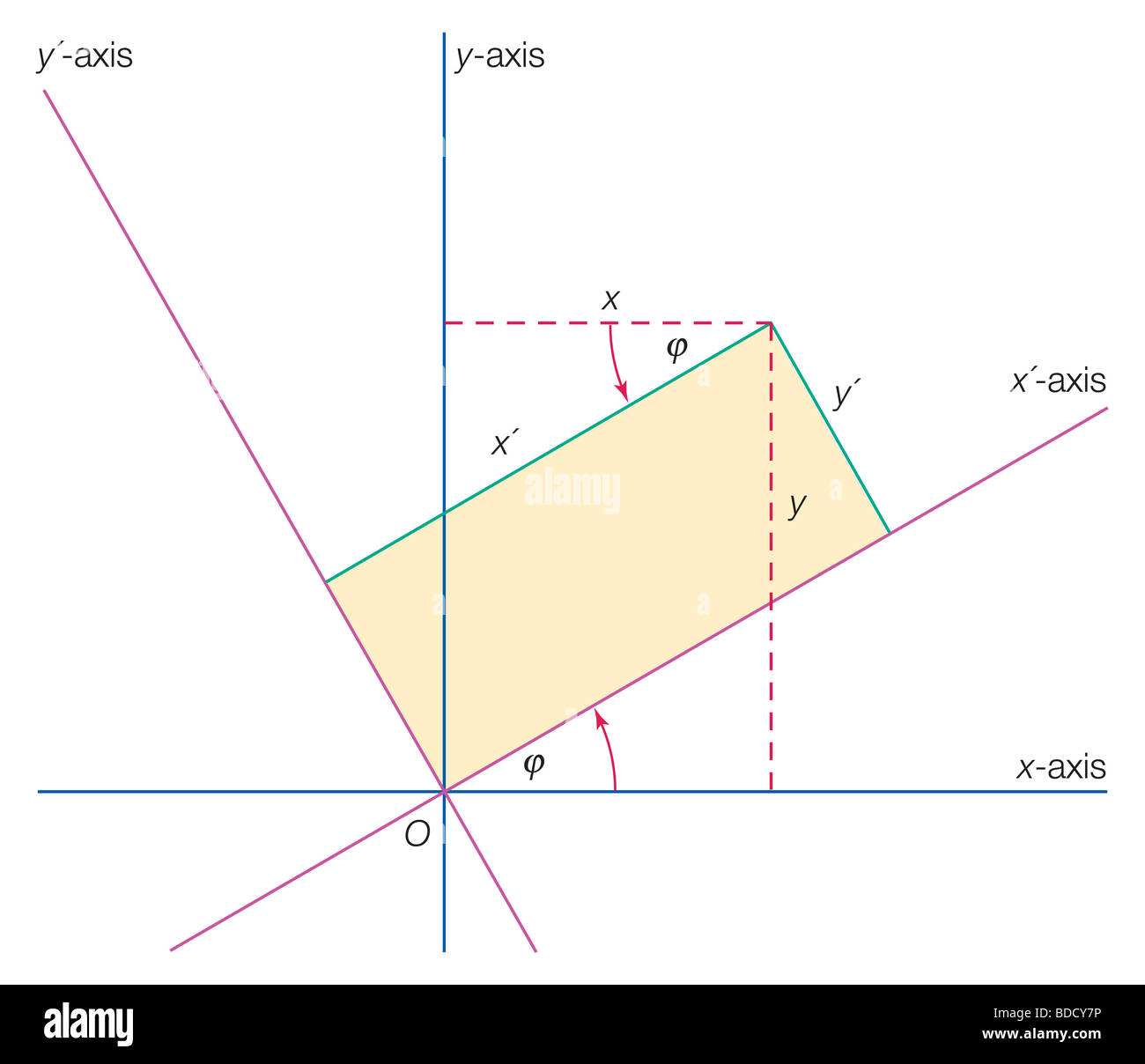 Achse drehen Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-achse-drehen-25485706.html
Achse drehen Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-achse-drehen-25485706.htmlRMBDCY7P–Achse drehen
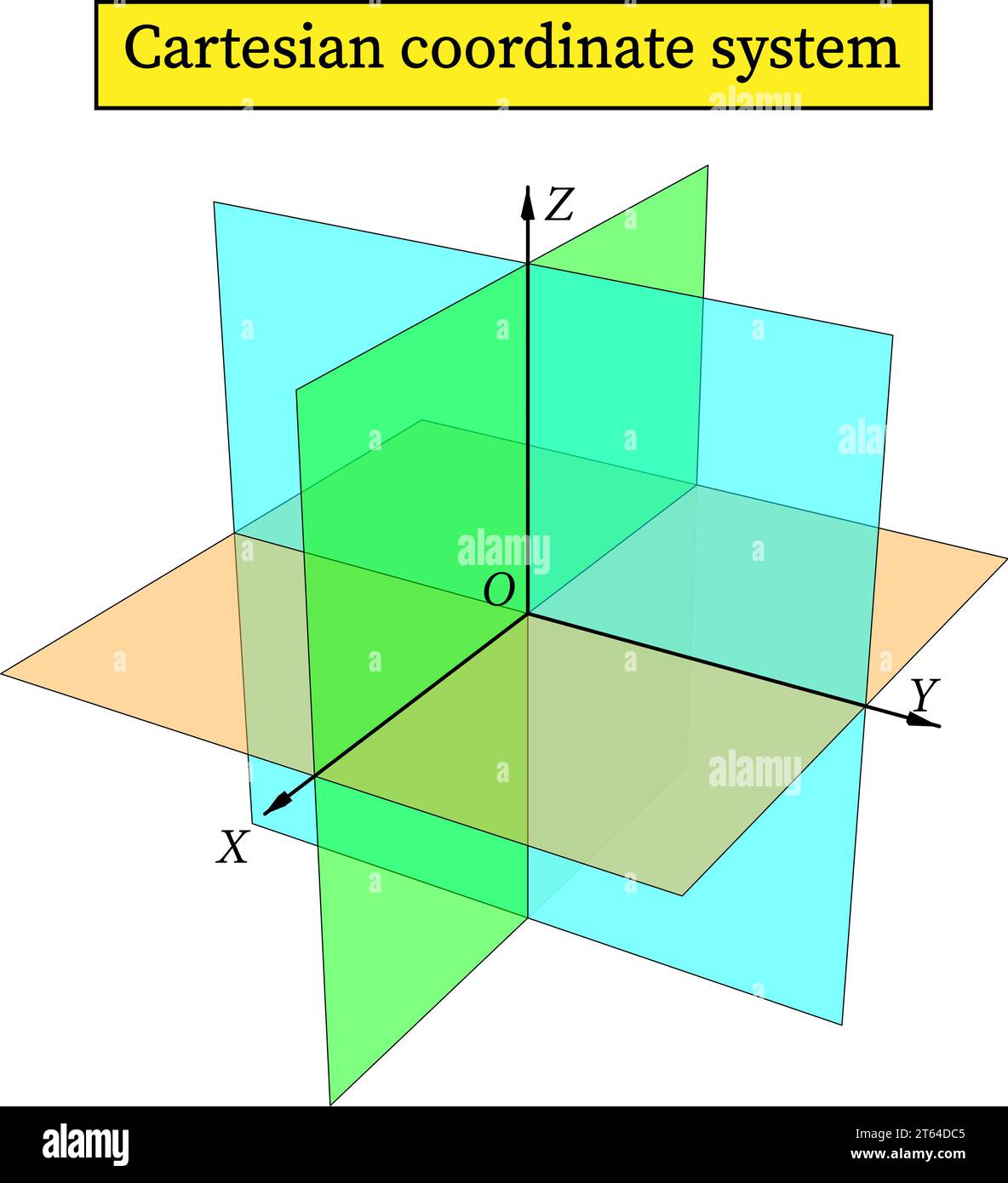 Der dreidimensionale euklidische Raum. Vektorabbildung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/der-dreidimensionale-euklidische-raum-vektorabbildung-image571728421.html
Der dreidimensionale euklidische Raum. Vektorabbildung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/der-dreidimensionale-euklidische-raum-vektorabbildung-image571728421.htmlRF2T64DC5–Der dreidimensionale euklidische Raum. Vektorabbildung
 Senkrecht Symbol auf weißem Hintergrund. Einfaches element Abbildung kann von Zeichen Konzept. senkrecht Symbol Design. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/senkrecht-symbol-auf-weissem-hintergrund-einfaches-element-abbildung-kann-von-zeichen-konzept-senkrecht-symbol-design-image336390790.html
Senkrecht Symbol auf weißem Hintergrund. Einfaches element Abbildung kann von Zeichen Konzept. senkrecht Symbol Design. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/senkrecht-symbol-auf-weissem-hintergrund-einfaches-element-abbildung-kann-von-zeichen-konzept-senkrecht-symbol-design-image336390790.htmlRF2AF7WTP–Senkrecht Symbol auf weißem Hintergrund. Einfaches element Abbildung kann von Zeichen Konzept. senkrecht Symbol Design.
 Kartesischen Achsen Symbol, outline Style Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesischen-achsen-symbol-outline-style-image259800870.html
Kartesischen Achsen Symbol, outline Style Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesischen-achsen-symbol-outline-style-image259800870.htmlRFW2JXJE–Kartesischen Achsen Symbol, outline Style
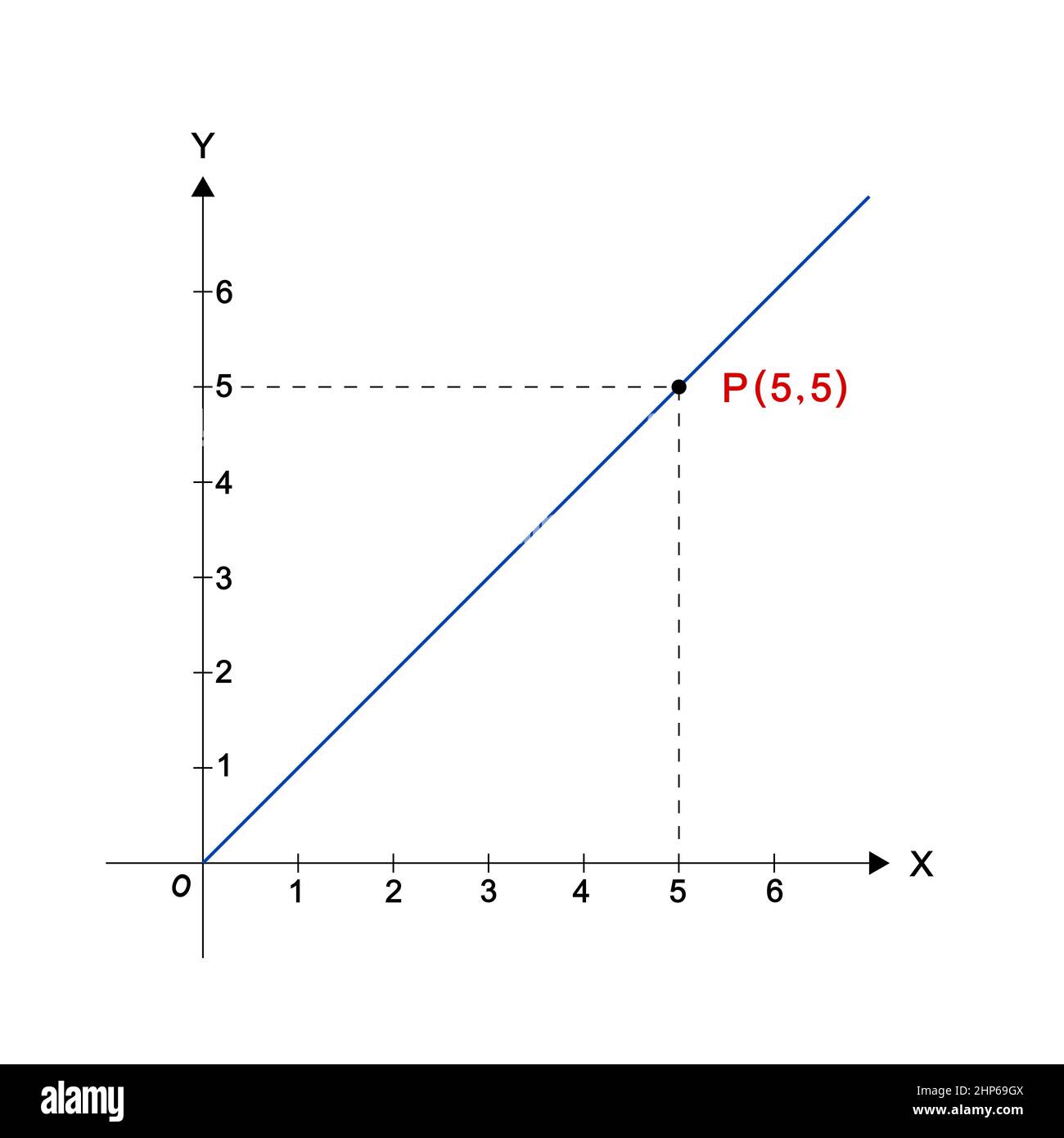 Geordnetes Paar in der kartesischen Ebene, xy positive Achse 1st Quadrant Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/geordnetes-paar-in-der-kartesischen-ebene-xy-positive-achse-1st-quadrant-image461131242.html
Geordnetes Paar in der kartesischen Ebene, xy positive Achse 1st Quadrant Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/geordnetes-paar-in-der-kartesischen-ebene-xy-positive-achse-1st-quadrant-image461131242.htmlRF2HP69GX–Geordnetes Paar in der kartesischen Ebene, xy positive Achse 1st Quadrant
 Sommer-Hausaufgaben Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-sommer-hausaufgaben-101056559.html
Sommer-Hausaufgaben Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-sommer-hausaufgaben-101056559.htmlRMFTBEJR–Sommer-Hausaufgaben
 kartesisches Koordinatensystem Vektor-Symbol editierbare Konturumrisssymbole für Web und Mobil Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-vektor-symbol-editierbare-konturumrisssymbole-fur-web-und-mobil-image397298069.html
kartesisches Koordinatensystem Vektor-Symbol editierbare Konturumrisssymbole für Web und Mobil Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-vektor-symbol-editierbare-konturumrisssymbole-fur-web-und-mobil-image397298069.htmlRF2E2ADMN–kartesisches Koordinatensystem Vektor-Symbol editierbare Konturumrisssymbole für Web und Mobil
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-97001455.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-97001455.htmlRFFHPP9K–Grundlegende Wissenschaft und des Wissens Symbole
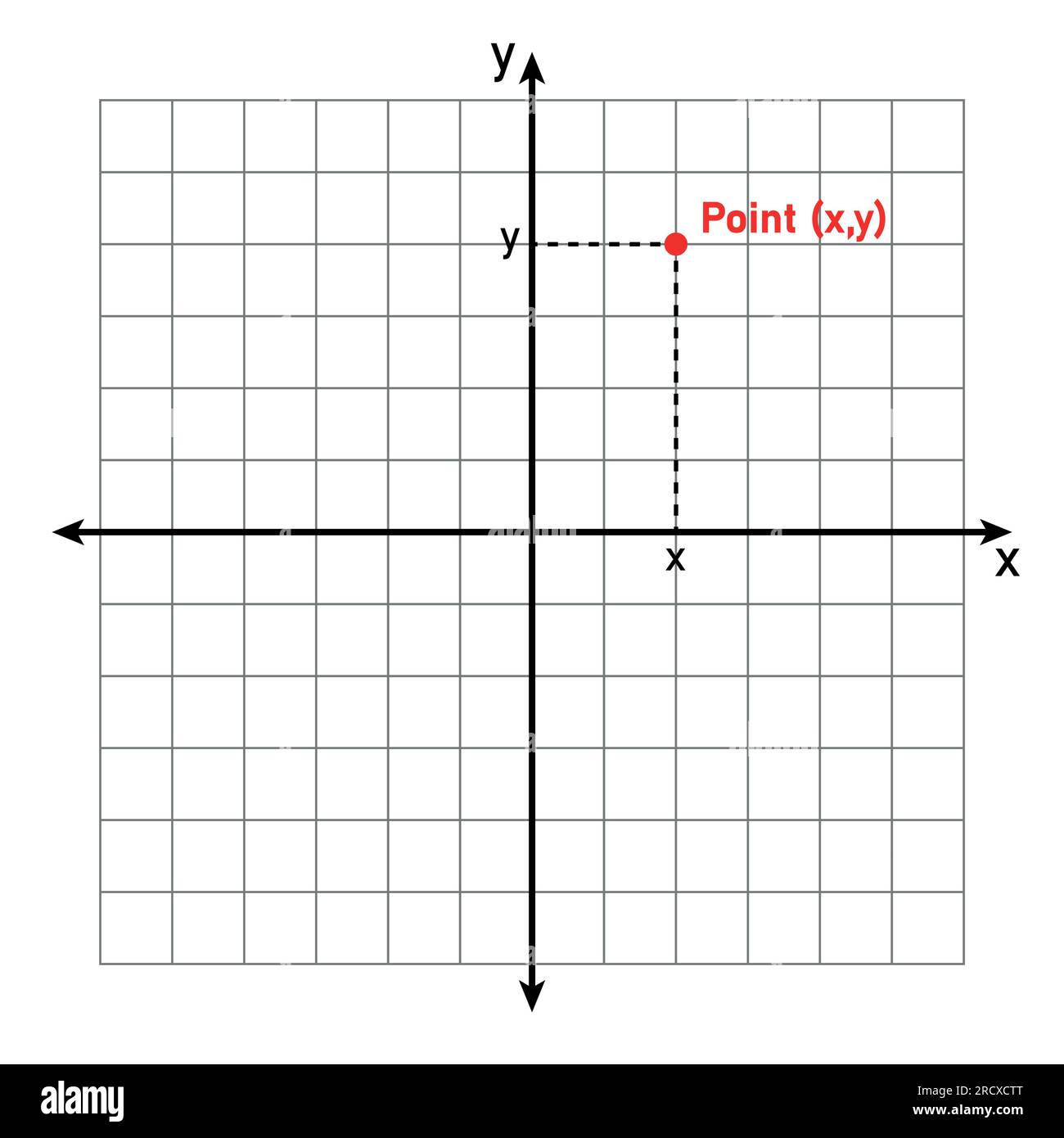 Die Punkte in der Koordinatenebene in der Mathematik. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-image558688504.html
Die Punkte in der Koordinatenebene in der Mathematik. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-image558688504.htmlRF2RCXCTT–Die Punkte in der Koordinatenebene in der Mathematik.
 Kartesischen Koordinatensystem an Tafel Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesischen-koordinatensystem-an-tafel-75592353.html
Kartesischen Koordinatensystem an Tafel Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesischen-koordinatensystem-an-tafel-75592353.htmlRFEAYEPW–Kartesischen Koordinatensystem an Tafel
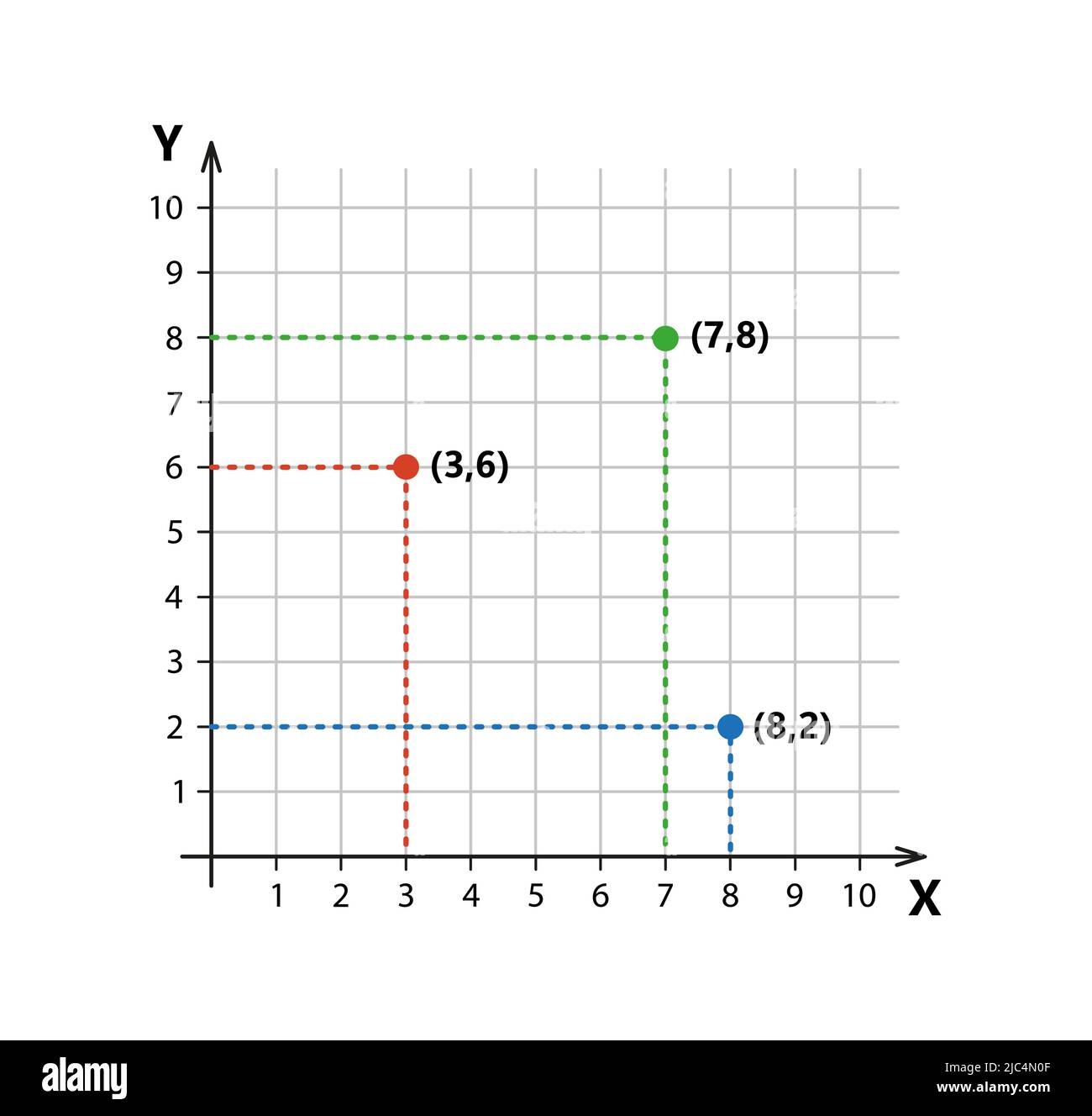 Kartesisches Koordinatensystem in zwei Dimensionen mit Probenpunkten. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-in-zwei-dimensionen-mit-probenpunkten-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vektor-image472160095.html
Kartesisches Koordinatensystem in zwei Dimensionen mit Probenpunkten. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-in-zwei-dimensionen-mit-probenpunkten-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vektor-image472160095.htmlRF2JC4N0F–Kartesisches Koordinatensystem in zwei Dimensionen mit Probenpunkten. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vektor
![Advanced calculus;. Stammaktien, die Eigenschaften, die ein-f 0 = a und a0=0 und A/0 isimpossible. Darüber, ob ein Produkt nach hinten verschwindet, entweder ein oder ft verschwindet. Für angenommen [a+bi] [c+ di]=(ac-bd) + (AD +) i= 0. Dann ac-bd = 0 und Ad + = 0, (12) aus denen folgt, dass entweder a = b = 0 und c = d = 0. Von thefact, dass ein Produkt nicht verschwinden, es sei denn, einer der Faktoren, die die normalen Gesetze der Stornierung vanishesfollow. Kurz gesagt, alle elementarylaws von real Algebra halten auch für die Algebra der komplexen Zahlen. Durch die Übernahme einer Reihe von kartesischen Koordinaten in die £ c?/-Ebene und Asso-c Stockfoto Advanced calculus;. Stammaktien, die Eigenschaften, die ein-f 0 = a und a0=0 und A/0 isimpossible. Darüber, ob ein Produkt nach hinten verschwindet, entweder ein oder ft verschwindet. Für angenommen [a+bi] [c+ di]=(ac-bd) + (AD +) i= 0. Dann ac-bd = 0 und Ad + = 0, (12) aus denen folgt, dass entweder a = b = 0 und c = d = 0. Von thefact, dass ein Produkt nicht verschwinden, es sei denn, einer der Faktoren, die die normalen Gesetze der Stornierung vanishesfollow. Kurz gesagt, alle elementarylaws von real Algebra halten auch für die Algebra der komplexen Zahlen. Durch die Übernahme einer Reihe von kartesischen Koordinaten in die £ c?/-Ebene und Asso-c Stockfoto](https://c8.alamy.com/compde/2aj32y0/advanced-calculus-stammaktien-die-eigenschaften-die-ein-f-0-=-a-und-a0=0-und-a0-isimpossible-daruber-ob-ein-produkt-nach-hinten-verschwindet-entweder-ein-oder-ft-verschwindet-fur-angenommen-abi-c-di-=ac-bd-ad-i=-0-dann-ac-bd-=-0-und-ad-=-0-12-aus-denen-folgt-dass-entweder-a-=-b-=-0-und-c-=-d-=-0-von-thefact-dass-ein-produkt-nicht-verschwinden-es-sei-denn-einer-der-faktoren-die-die-normalen-gesetze-der-stornierung-vanishesfollow-kurz-gesagt-alle-elementarylaws-von-real-algebra-halten-auch-fur-die-algebra-der-komplexen-zahlen-durch-die-ubernahme-einer-reihe-von-kartesischen-koordinaten-in-die-c-ebene-und-asso-c-2aj32y0.jpg) Advanced calculus;. Stammaktien, die Eigenschaften, die ein-f 0 = a und a0=0 und A/0 isimpossible. Darüber, ob ein Produkt nach hinten verschwindet, entweder ein oder ft verschwindet. Für angenommen [a+bi] [c+ di]=(ac-bd) + (AD +) i= 0. Dann ac-bd = 0 und Ad + = 0, (12) aus denen folgt, dass entweder a = b = 0 und c = d = 0. Von thefact, dass ein Produkt nicht verschwinden, es sei denn, einer der Faktoren, die die normalen Gesetze der Stornierung vanishesfollow. Kurz gesagt, alle elementarylaws von real Algebra halten auch für die Algebra der komplexen Zahlen. Durch die Übernahme einer Reihe von kartesischen Koordinaten in die £ c?/-Ebene und Asso-c Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/advanced-calculus-stammaktien-die-eigenschaften-die-ein-f-0-=-a-und-a0=0-und-a0-isimpossible-daruber-ob-ein-produkt-nach-hinten-verschwindet-entweder-ein-oder-ft-verschwindet-fur-angenommen-abi-c-di-=ac-bd-ad-i=-0-dann-ac-bd-=-0-und-ad-=-0-12-aus-denen-folgt-dass-entweder-a-=-b-=-0-und-c-=-d-=-0-von-thefact-dass-ein-produkt-nicht-verschwinden-es-sei-denn-einer-der-faktoren-die-die-normalen-gesetze-der-stornierung-vanishesfollow-kurz-gesagt-alle-elementarylaws-von-real-algebra-halten-auch-fur-die-algebra-der-komplexen-zahlen-durch-die-ubernahme-einer-reihe-von-kartesischen-koordinaten-in-die-c-ebene-und-asso-c-image338128980.html
Advanced calculus;. Stammaktien, die Eigenschaften, die ein-f 0 = a und a0=0 und A/0 isimpossible. Darüber, ob ein Produkt nach hinten verschwindet, entweder ein oder ft verschwindet. Für angenommen [a+bi] [c+ di]=(ac-bd) + (AD +) i= 0. Dann ac-bd = 0 und Ad + = 0, (12) aus denen folgt, dass entweder a = b = 0 und c = d = 0. Von thefact, dass ein Produkt nicht verschwinden, es sei denn, einer der Faktoren, die die normalen Gesetze der Stornierung vanishesfollow. Kurz gesagt, alle elementarylaws von real Algebra halten auch für die Algebra der komplexen Zahlen. Durch die Übernahme einer Reihe von kartesischen Koordinaten in die £ c?/-Ebene und Asso-c Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/advanced-calculus-stammaktien-die-eigenschaften-die-ein-f-0-=-a-und-a0=0-und-a0-isimpossible-daruber-ob-ein-produkt-nach-hinten-verschwindet-entweder-ein-oder-ft-verschwindet-fur-angenommen-abi-c-di-=ac-bd-ad-i=-0-dann-ac-bd-=-0-und-ad-=-0-12-aus-denen-folgt-dass-entweder-a-=-b-=-0-und-c-=-d-=-0-von-thefact-dass-ein-produkt-nicht-verschwinden-es-sei-denn-einer-der-faktoren-die-die-normalen-gesetze-der-stornierung-vanishesfollow-kurz-gesagt-alle-elementarylaws-von-real-algebra-halten-auch-fur-die-algebra-der-komplexen-zahlen-durch-die-ubernahme-einer-reihe-von-kartesischen-koordinaten-in-die-c-ebene-und-asso-c-image338128980.htmlRM2AJ32Y0–Advanced calculus;. Stammaktien, die Eigenschaften, die ein-f 0 = a und a0=0 und A/0 isimpossible. Darüber, ob ein Produkt nach hinten verschwindet, entweder ein oder ft verschwindet. Für angenommen [a+bi] [c+ di]=(ac-bd) + (AD +) i= 0. Dann ac-bd = 0 und Ad + = 0, (12) aus denen folgt, dass entweder a = b = 0 und c = d = 0. Von thefact, dass ein Produkt nicht verschwinden, es sei denn, einer der Faktoren, die die normalen Gesetze der Stornierung vanishesfollow. Kurz gesagt, alle elementarylaws von real Algebra halten auch für die Algebra der komplexen Zahlen. Durch die Übernahme einer Reihe von kartesischen Koordinaten in die £ c?/-Ebene und Asso-c
 Es wird ein xy-Raster/Diagramm mit Rasterlinien angezeigt. Es ist das kartesische Koordinatensystem mit geraden Schritten von -10 bis 10 beschrifteten, Vintage-Linien-Zeichnungen o Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/es-wird-ein-xy-rasterdiagramm-mit-rasterlinien-angezeigt-es-ist-das-kartesische-koordinatensystem-mit-geraden-schritten-von-10-bis-10-beschrifteten-vintage-linien-zeichnungen-o-image348663942.html
Es wird ein xy-Raster/Diagramm mit Rasterlinien angezeigt. Es ist das kartesische Koordinatensystem mit geraden Schritten von -10 bis 10 beschrifteten, Vintage-Linien-Zeichnungen o Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/es-wird-ein-xy-rasterdiagramm-mit-rasterlinien-angezeigt-es-ist-das-kartesische-koordinatensystem-mit-geraden-schritten-von-10-bis-10-beschrifteten-vintage-linien-zeichnungen-o-image348663942.htmlRF2B770BJ–Es wird ein xy-Raster/Diagramm mit Rasterlinien angezeigt. Es ist das kartesische Koordinatensystem mit geraden Schritten von -10 bis 10 beschrifteten, Vintage-Linien-Zeichnungen o
 Auf die weiße Fläche, eine Koordinatenachse geplottet mit Leinsamen. Eine aufsteigende Diagramm ist aus Süßigkeiten. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-auf-die-weisse-flache-eine-koordinatenachse-geplottet-mit-leinsamen-eine-aufsteigende-diagramm-ist-aus-sussigkeiten-310970212.html
Auf die weiße Fläche, eine Koordinatenachse geplottet mit Leinsamen. Eine aufsteigende Diagramm ist aus Süßigkeiten. Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-auf-die-weisse-flache-eine-koordinatenachse-geplottet-mit-leinsamen-eine-aufsteigende-diagramm-ist-aus-sussigkeiten-310970212.htmlRFS1WWK0–Auf die weiße Fläche, eine Koordinatenachse geplottet mit Leinsamen. Eine aufsteigende Diagramm ist aus Süßigkeiten.
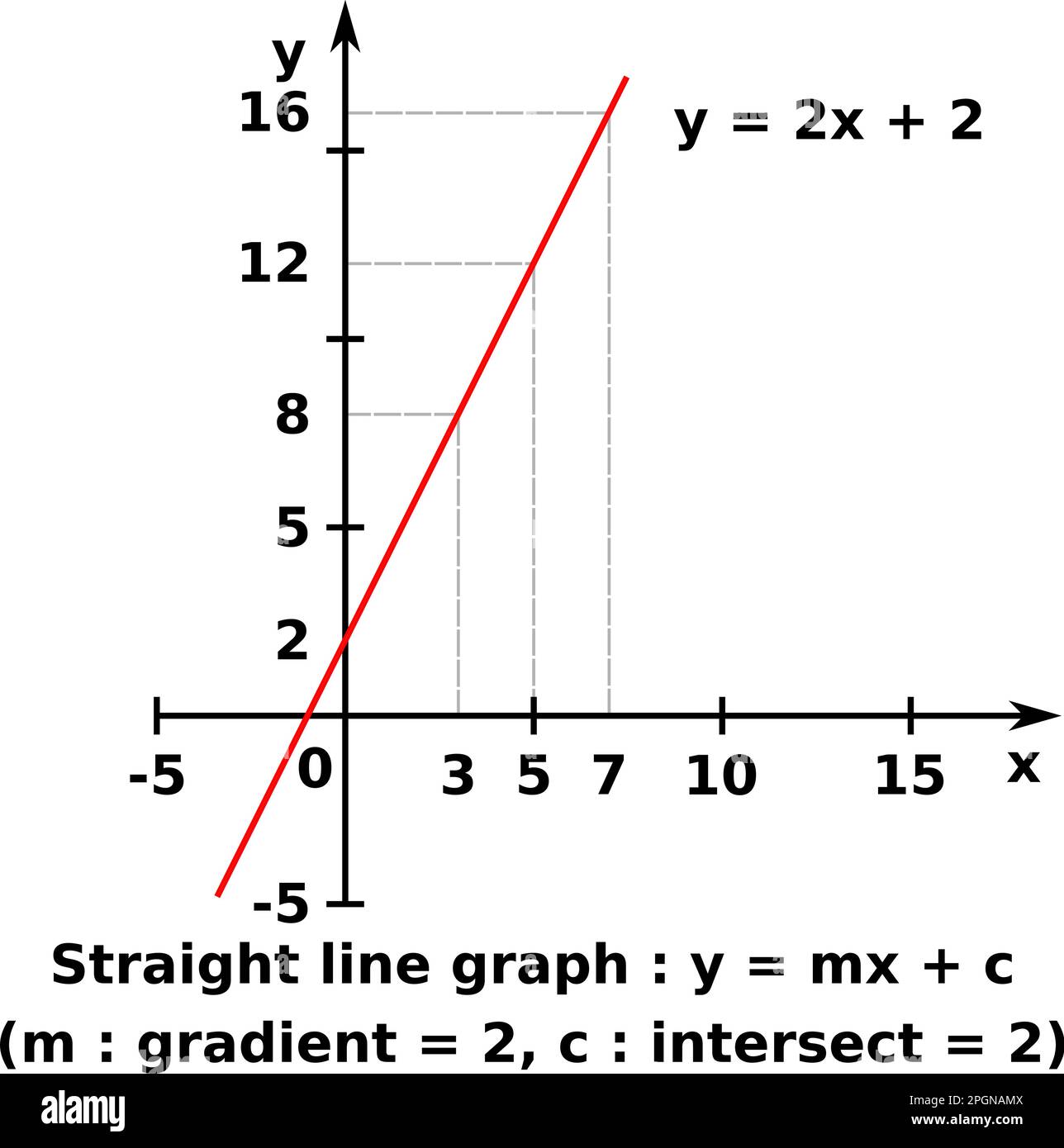 Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = 2x + 2 Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektorgrafik-eines-diagramms-von-x-gegen-y-einer-linearen-funktion-die-dargestellte-formel-ist-y-=-2x-2-image543825322.html
Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = 2x + 2 Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektorgrafik-eines-diagramms-von-x-gegen-y-einer-linearen-funktion-die-dargestellte-formel-ist-y-=-2x-2-image543825322.htmlRF2PGNAMX–Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = 2x + 2
 Der dreidimensionale euklidische Raum. Vektorabbildung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/der-dreidimensionale-euklidische-raum-vektorabbildung-image571728465.html
Der dreidimensionale euklidische Raum. Vektorabbildung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/der-dreidimensionale-euklidische-raum-vektorabbildung-image571728465.htmlRF2T64DDN–Der dreidimensionale euklidische Raum. Vektorabbildung
 Vektordarstellung des drei-Achsen-Koordinatensystems Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektordarstellung-des-drei-achsen-koordinatensystems-image571427556.html
Vektordarstellung des drei-Achsen-Koordinatensystems Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektordarstellung-des-drei-achsen-koordinatensystems-image571427556.htmlRF2T5JNK0–Vektordarstellung des drei-Achsen-Koordinatensystems
 Diagramm des Ursprungs der kartesischen Ebene und 4 Quadranten, Kreis mit dem Zentrum am Schnittpunkt der x- und y-Achse Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/diagramm-des-ursprungs-der-kartesischen-ebene-und-4-quadranten-kreis-mit-dem-zentrum-am-schnittpunkt-der-x-und-y-achse-image461131425.html
Diagramm des Ursprungs der kartesischen Ebene und 4 Quadranten, Kreis mit dem Zentrum am Schnittpunkt der x- und y-Achse Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/diagramm-des-ursprungs-der-kartesischen-ebene-und-4-quadranten-kreis-mit-dem-zentrum-am-schnittpunkt-der-x-und-y-achse-image461131425.htmlRF2HP69RD–Diagramm des Ursprungs der kartesischen Ebene und 4 Quadranten, Kreis mit dem Zentrum am Schnittpunkt der x- und y-Achse
 Symbol für kartesische Achsen. Kontur kartesischen Achsen Vektor Symbol Farbe flach isoliert Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/symbol-fur-kartesische-achsen-kontur-kartesischen-achsen-vektor-symbol-farbe-flach-isoliert-image443330732.html
Symbol für kartesische Achsen. Kontur kartesischen Achsen Vektor Symbol Farbe flach isoliert Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/symbol-fur-kartesische-achsen-kontur-kartesischen-achsen-vektor-symbol-farbe-flach-isoliert-image443330732.htmlRF2GN7CTC–Symbol für kartesische Achsen. Kontur kartesischen Achsen Vektor Symbol Farbe flach isoliert
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96820374.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96820374.htmlRFFHEFAE–Grundlegende Wissenschaft und des Wissens Symbole
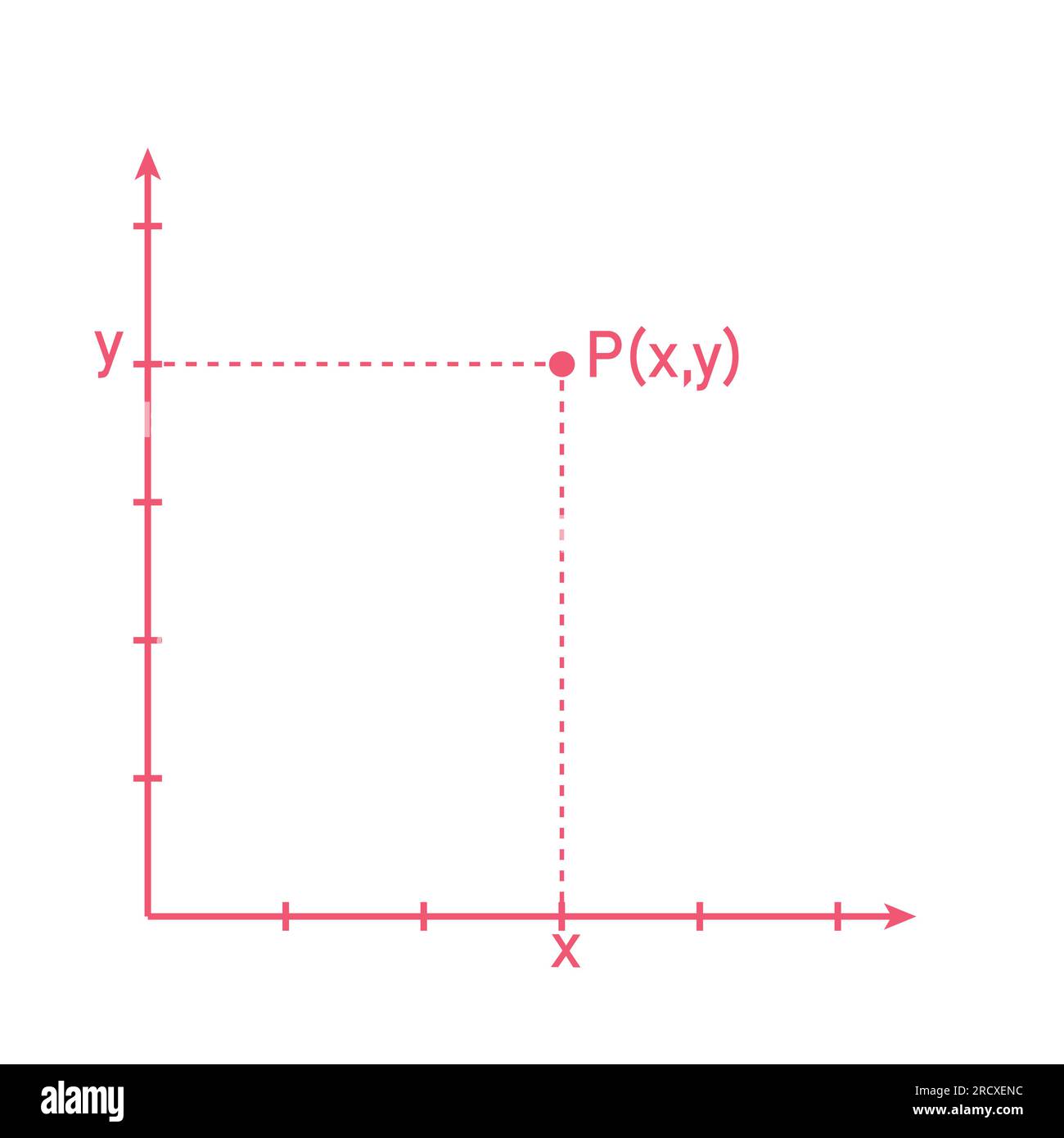 Die Punkte in der Koordinatenebene in der Mathematik. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-image558689976.html
Die Punkte in der Koordinatenebene in der Mathematik. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-image558689976.htmlRF2RCXENC–Die Punkte in der Koordinatenebene in der Mathematik.
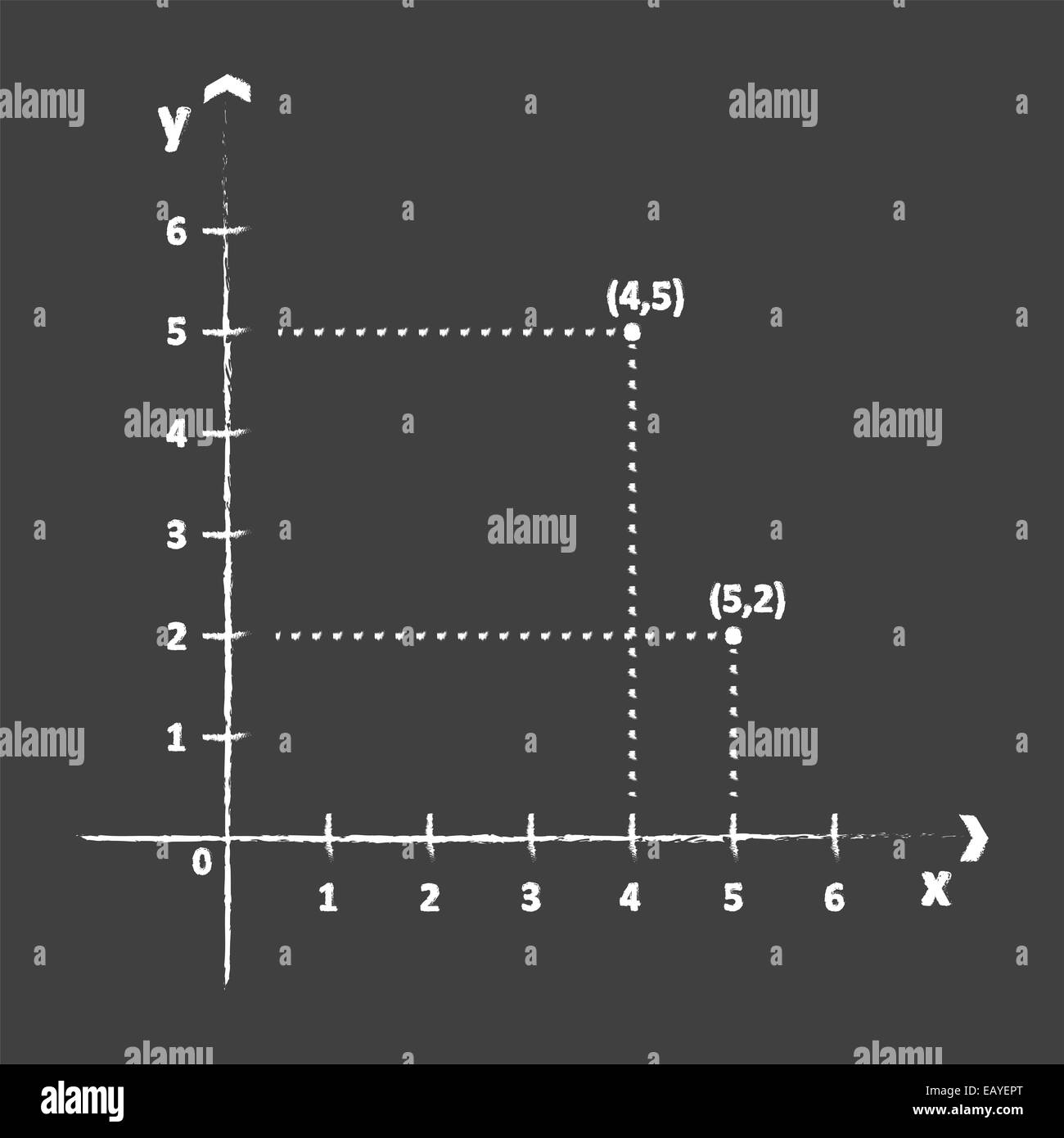 Kartesischen Koordinatensystem an Tafel Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesischen-koordinatensystem-an-tafel-75592352.html
Kartesischen Koordinatensystem an Tafel Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-kartesischen-koordinatensystem-an-tafel-75592352.htmlRFEAYEPT–Kartesischen Koordinatensystem an Tafel
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-vektor-image503368175.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-vektor-image503368175.htmlRF2M6XB6R–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y. Vektor
 Eine elementare Abhandlung über Koordinatensystem Geometrie der drei Dimensionen. 1 kongruent Ochsen und drehte sich dann durch die givenangle, ist die positive Richtung auf. In der Abbildung, u, ≪p, z sind alle positiv. Wenn die kartesischen Koordinaten von P sind x, y, z, x, y, 0 Nsind. Wenn wir uns nur Punkte in der Ebene XOY, die kartesischen Koordinaten von N sind x, y und die Polar, u, ≪s. Deshalb x-u cos(p, y=u Sünde 0; u2=x2+y2, tan 0 = y/x.. 6. Polarkoordinaten. Nehmen wir an, dass die Position der Ebene OZPN (Abb. 2), ist durch einen bestimmten valueof< bestimmt worden; p, dann können wir definieren die Posi Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/eine-elementare-abhandlung-uber-koordinatensystem-geometrie-der-drei-dimensionen-1-kongruent-ochsen-und-drehte-sich-dann-durch-die-givenangle-ist-die-positive-richtung-auf-in-der-abbildung-u-ltp-z-sind-alle-positiv-wenn-die-kartesischen-koordinaten-von-p-sind-x-y-z-x-y-0-nsind-wenn-wir-uns-nur-punkte-in-der-ebene-xoy-die-kartesischen-koordinaten-von-n-sind-x-y-und-die-polar-u-lts-deshalb-x-u-cosp-y=u-sunde-0-u2=x2y2-tan-0-=-yx-6-polarkoordinaten-nehmen-wir-an-dass-die-position-der-ebene-ozpn-abb-2-ist-durch-einen-bestimmten-valueoflt-bestimmt-worden-p-dann-konnen-wir-definieren-die-posi-image340014255.html
Eine elementare Abhandlung über Koordinatensystem Geometrie der drei Dimensionen. 1 kongruent Ochsen und drehte sich dann durch die givenangle, ist die positive Richtung auf. In der Abbildung, u, ≪p, z sind alle positiv. Wenn die kartesischen Koordinaten von P sind x, y, z, x, y, 0 Nsind. Wenn wir uns nur Punkte in der Ebene XOY, die kartesischen Koordinaten von N sind x, y und die Polar, u, ≪s. Deshalb x-u cos(p, y=u Sünde 0; u2=x2+y2, tan 0 = y/x.. 6. Polarkoordinaten. Nehmen wir an, dass die Position der Ebene OZPN (Abb. 2), ist durch einen bestimmten valueof< bestimmt worden; p, dann können wir definieren die Posi Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/eine-elementare-abhandlung-uber-koordinatensystem-geometrie-der-drei-dimensionen-1-kongruent-ochsen-und-drehte-sich-dann-durch-die-givenangle-ist-die-positive-richtung-auf-in-der-abbildung-u-ltp-z-sind-alle-positiv-wenn-die-kartesischen-koordinaten-von-p-sind-x-y-z-x-y-0-nsind-wenn-wir-uns-nur-punkte-in-der-ebene-xoy-die-kartesischen-koordinaten-von-n-sind-x-y-und-die-polar-u-lts-deshalb-x-u-cosp-y=u-sunde-0-u2=x2y2-tan-0-=-yx-6-polarkoordinaten-nehmen-wir-an-dass-die-position-der-ebene-ozpn-abb-2-ist-durch-einen-bestimmten-valueoflt-bestimmt-worden-p-dann-konnen-wir-definieren-die-posi-image340014255.htmlRM2AN4YJ7–Eine elementare Abhandlung über Koordinatensystem Geometrie der drei Dimensionen. 1 kongruent Ochsen und drehte sich dann durch die givenangle, ist die positive Richtung auf. In der Abbildung, u, ≪p, z sind alle positiv. Wenn die kartesischen Koordinaten von P sind x, y, z, x, y, 0 Nsind. Wenn wir uns nur Punkte in der Ebene XOY, die kartesischen Koordinaten von N sind x, y und die Polar, u, ≪s. Deshalb x-u cos(p, y=u Sünde 0; u2=x2+y2, tan 0 = y/x.. 6. Polarkoordinaten. Nehmen wir an, dass die Position der Ebene OZPN (Abb. 2), ist durch einen bestimmten valueof< bestimmt worden; p, dann können wir definieren die Posi
 Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = x + 2 Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektorgrafik-eines-diagramms-von-x-gegen-y-einer-linearen-funktion-die-dargestellte-formel-ist-y-=-x-2-image543825244.html
Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = x + 2 Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektorgrafik-eines-diagramms-von-x-gegen-y-einer-linearen-funktion-die-dargestellte-formel-ist-y-=-x-2-image543825244.htmlRF2PGNAJ4–Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = x + 2
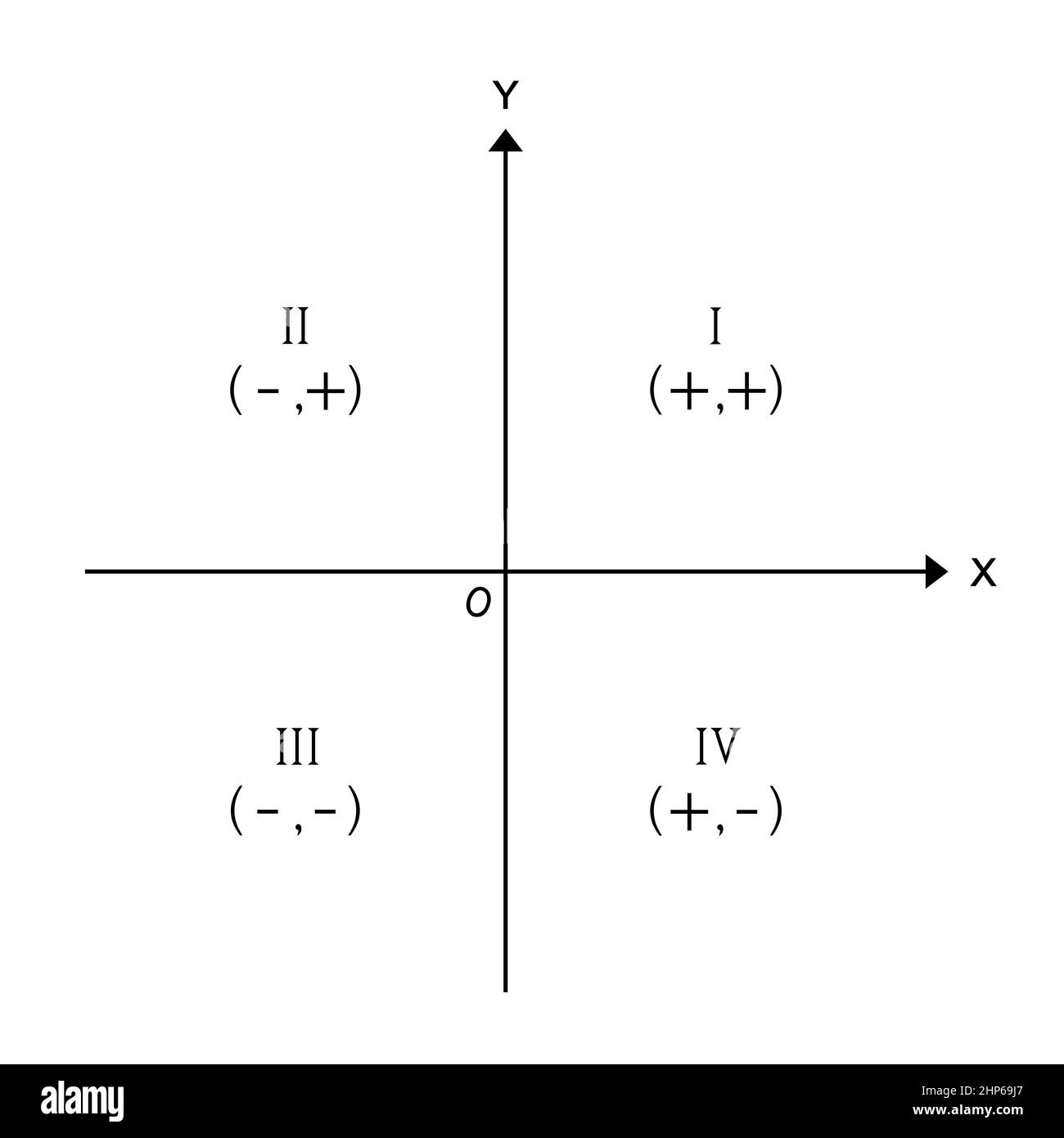 Vier Quadranten und Zeichen treffen auf der Koordinatenebene aufeinander Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vier-quadranten-und-zeichen-treffen-auf-der-koordinatenebene-aufeinander-image461131279.html
Vier Quadranten und Zeichen treffen auf der Koordinatenebene aufeinander Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vier-quadranten-und-zeichen-treffen-auf-der-koordinatenebene-aufeinander-image461131279.htmlRF2HP69J7–Vier Quadranten und Zeichen treffen auf der Koordinatenebene aufeinander
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96975906.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96975906.htmlRFFHNHN6–Grundlegende Wissenschaft und des Wissens Symbole
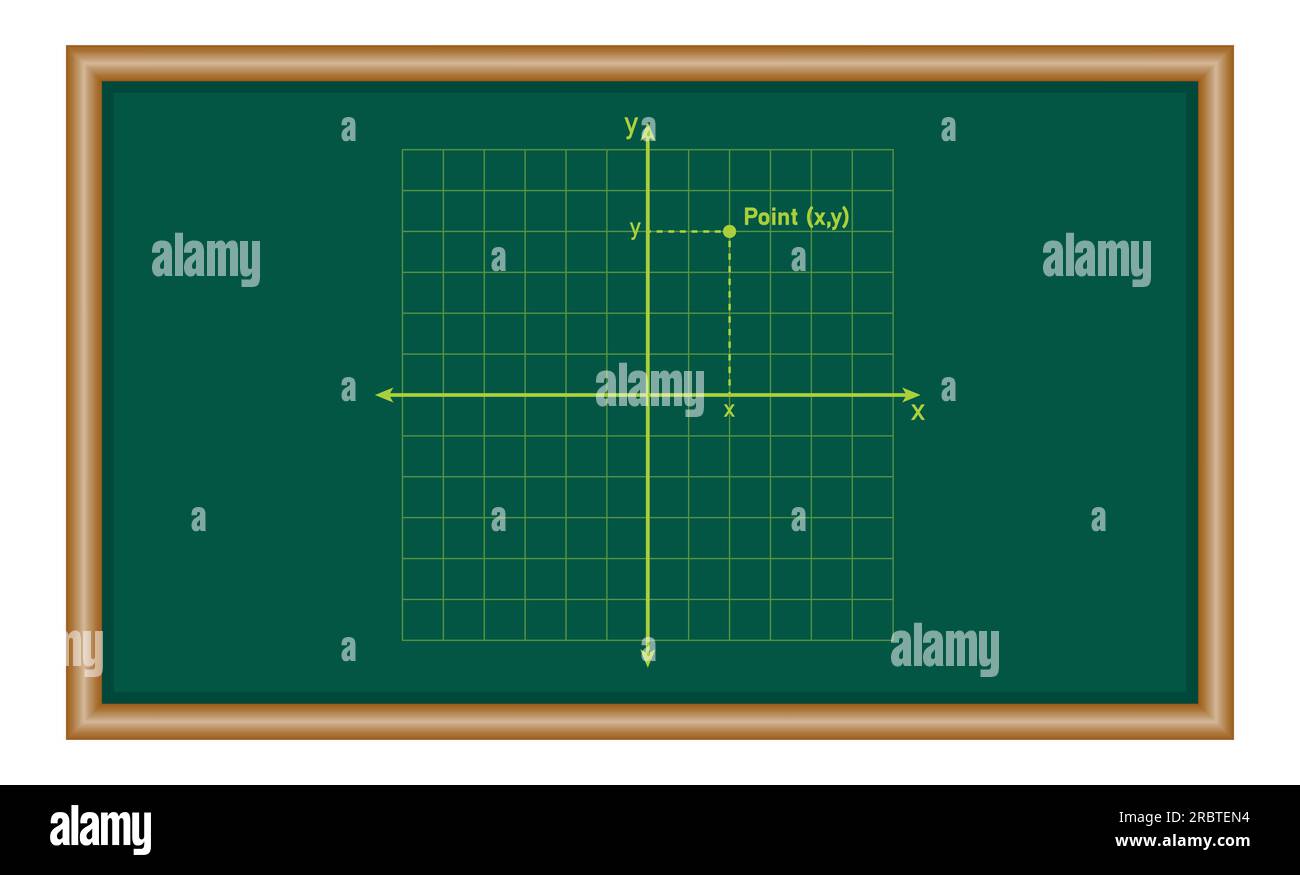 Das kartesische Koordinatensystem in der Ebene. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/das-kartesische-koordinatensystem-in-der-ebene-mathematische-ressourcen-fur-lehrer-und-schuler-image558031408.html
Das kartesische Koordinatensystem in der Ebene. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/das-kartesische-koordinatensystem-in-der-ebene-mathematische-ressourcen-fur-lehrer-und-schuler-image558031408.htmlRF2RBTEN4–Das kartesische Koordinatensystem in der Ebene. Mathematische Ressourcen für Lehrer und Schüler.
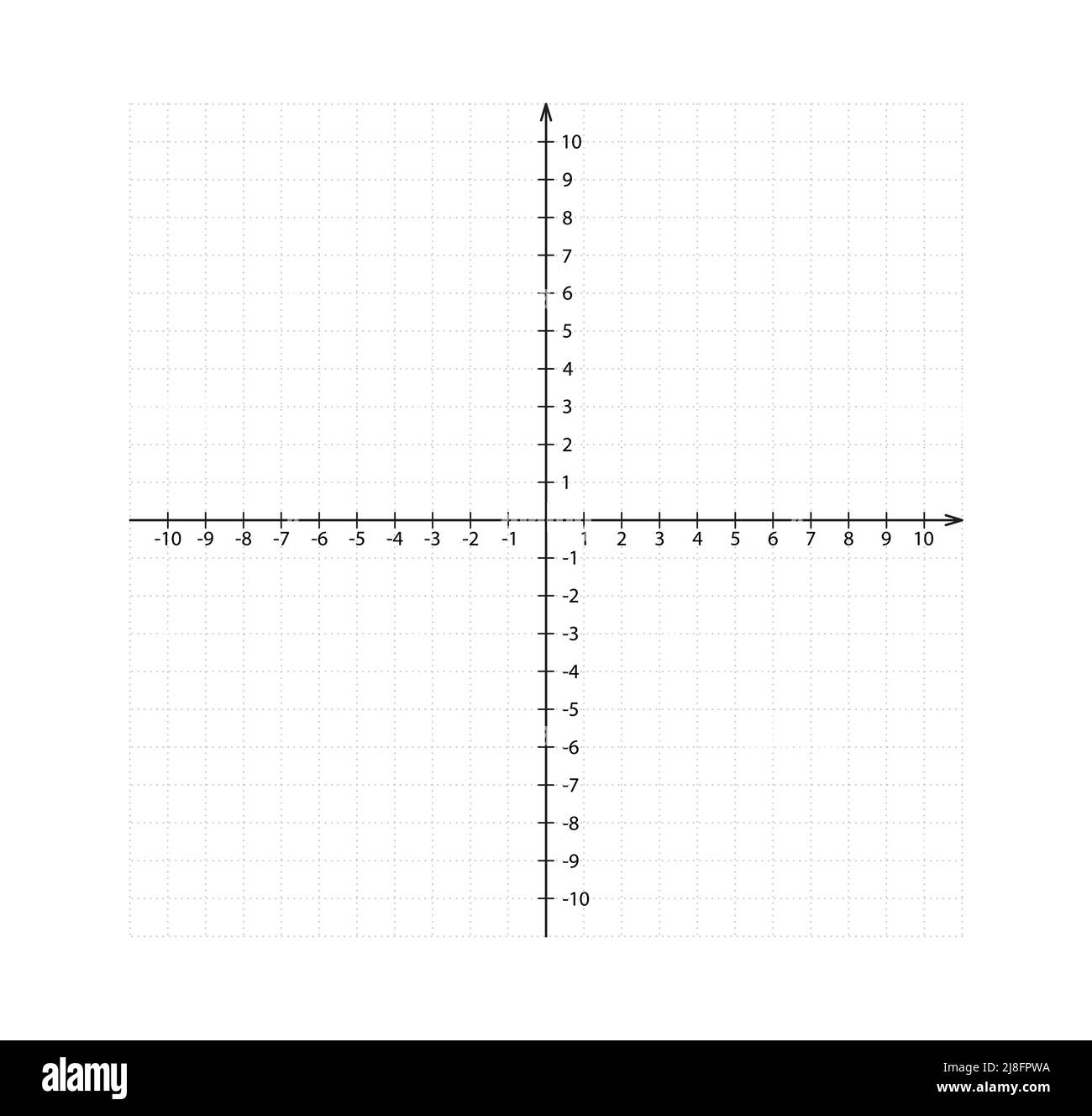 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-vektor-image469944422.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-vektor-image469944422.htmlRF2J8FPWA–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y. Vektor
![. Ebene und feste analytische Geometrie; ein elementares Lehrbuch. n schräge Koordinaten.die Ergebnisse sind daher allgemein, und wird auf eithersystem von kartesischen Koordinaten gelten. 14. Harmonische Teilung. - Wenn die Linie A C durch die Punkte B und D geteilt wird, intern-. Und extern, im gleichen Zahlenverhältnis, oder so, dass -- = --, die Linie AC wird gesagt, um har-jd c U o monically geteilt werden. Cii. II, § 14] DER PUNKT 17 Lassen Sie den Kursteilnehmer zeigen, daß die Linie BD dann harmonisch durch die Punkte C und A geteilt wird oder so, daß BC = BACD AD die vier Punkte A, B, C und D gesagt werden, um einen harmonischen Bereich zu bilden. Wenn Stockfoto . Ebene und feste analytische Geometrie; ein elementares Lehrbuch. n schräge Koordinaten.die Ergebnisse sind daher allgemein, und wird auf eithersystem von kartesischen Koordinaten gelten. 14. Harmonische Teilung. - Wenn die Linie A C durch die Punkte B und D geteilt wird, intern-. Und extern, im gleichen Zahlenverhältnis, oder so, dass -- = --, die Linie AC wird gesagt, um har-jd c U o monically geteilt werden. Cii. II, § 14] DER PUNKT 17 Lassen Sie den Kursteilnehmer zeigen, daß die Linie BD dann harmonisch durch die Punkte C und A geteilt wird oder so, daß BC = BACD AD die vier Punkte A, B, C und D gesagt werden, um einen harmonischen Bereich zu bilden. Wenn Stockfoto](https://c8.alamy.com/compde/2cer5c9/ebene-und-feste-analytische-geometrie-ein-elementares-lehrbuch-n-schrage-koordinatendie-ergebnisse-sind-daher-allgemein-und-wird-auf-eithersystem-von-kartesischen-koordinaten-gelten-14-harmonische-teilung-wenn-die-linie-a-c-durch-die-punkte-b-und-d-geteilt-wird-intern-und-extern-im-gleichen-zahlenverhaltnis-oder-so-dass-=-die-linie-ac-wird-gesagt-um-har-jd-c-u-o-monically-geteilt-werden-cii-ii-14-der-punkt-17-lassen-sie-den-kursteilnehmer-zeigen-dass-die-linie-bd-dann-harmonisch-durch-die-punkte-c-und-a-geteilt-wird-oder-so-dass-bc-=-bacd-ad-die-vier-punkte-a-b-c-und-d-gesagt-werden-um-einen-harmonischen-bereich-zu-bilden-wenn-2cer5c9.jpg) . Ebene und feste analytische Geometrie; ein elementares Lehrbuch. n schräge Koordinaten.die Ergebnisse sind daher allgemein, und wird auf eithersystem von kartesischen Koordinaten gelten. 14. Harmonische Teilung. - Wenn die Linie A C durch die Punkte B und D geteilt wird, intern-. Und extern, im gleichen Zahlenverhältnis, oder so, dass -- = --, die Linie AC wird gesagt, um har-jd c U o monically geteilt werden. Cii. II, § 14] DER PUNKT 17 Lassen Sie den Kursteilnehmer zeigen, daß die Linie BD dann harmonisch durch die Punkte C und A geteilt wird oder so, daß BC = BACD AD die vier Punkte A, B, C und D gesagt werden, um einen harmonischen Bereich zu bilden. Wenn Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/ebene-und-feste-analytische-geometrie-ein-elementares-lehrbuch-n-schrage-koordinatendie-ergebnisse-sind-daher-allgemein-und-wird-auf-eithersystem-von-kartesischen-koordinaten-gelten-14-harmonische-teilung-wenn-die-linie-a-c-durch-die-punkte-b-und-d-geteilt-wird-intern-und-extern-im-gleichen-zahlenverhaltnis-oder-so-dass-=-die-linie-ac-wird-gesagt-um-har-jd-c-u-o-monically-geteilt-werden-cii-ii-14-der-punkt-17-lassen-sie-den-kursteilnehmer-zeigen-dass-die-linie-bd-dann-harmonisch-durch-die-punkte-c-und-a-geteilt-wird-oder-so-dass-bc-=-bacd-ad-die-vier-punkte-a-b-c-und-d-gesagt-werden-um-einen-harmonischen-bereich-zu-bilden-wenn-image370532073.html
. Ebene und feste analytische Geometrie; ein elementares Lehrbuch. n schräge Koordinaten.die Ergebnisse sind daher allgemein, und wird auf eithersystem von kartesischen Koordinaten gelten. 14. Harmonische Teilung. - Wenn die Linie A C durch die Punkte B und D geteilt wird, intern-. Und extern, im gleichen Zahlenverhältnis, oder so, dass -- = --, die Linie AC wird gesagt, um har-jd c U o monically geteilt werden. Cii. II, § 14] DER PUNKT 17 Lassen Sie den Kursteilnehmer zeigen, daß die Linie BD dann harmonisch durch die Punkte C und A geteilt wird oder so, daß BC = BACD AD die vier Punkte A, B, C und D gesagt werden, um einen harmonischen Bereich zu bilden. Wenn Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/ebene-und-feste-analytische-geometrie-ein-elementares-lehrbuch-n-schrage-koordinatendie-ergebnisse-sind-daher-allgemein-und-wird-auf-eithersystem-von-kartesischen-koordinaten-gelten-14-harmonische-teilung-wenn-die-linie-a-c-durch-die-punkte-b-und-d-geteilt-wird-intern-und-extern-im-gleichen-zahlenverhaltnis-oder-so-dass-=-die-linie-ac-wird-gesagt-um-har-jd-c-u-o-monically-geteilt-werden-cii-ii-14-der-punkt-17-lassen-sie-den-kursteilnehmer-zeigen-dass-die-linie-bd-dann-harmonisch-durch-die-punkte-c-und-a-geteilt-wird-oder-so-dass-bc-=-bacd-ad-die-vier-punkte-a-b-c-und-d-gesagt-werden-um-einen-harmonischen-bereich-zu-bilden-wenn-image370532073.htmlRM2CER5C9–. Ebene und feste analytische Geometrie; ein elementares Lehrbuch. n schräge Koordinaten.die Ergebnisse sind daher allgemein, und wird auf eithersystem von kartesischen Koordinaten gelten. 14. Harmonische Teilung. - Wenn die Linie A C durch die Punkte B und D geteilt wird, intern-. Und extern, im gleichen Zahlenverhältnis, oder so, dass -- = --, die Linie AC wird gesagt, um har-jd c U o monically geteilt werden. Cii. II, § 14] DER PUNKT 17 Lassen Sie den Kursteilnehmer zeigen, daß die Linie BD dann harmonisch durch die Punkte C und A geteilt wird oder so, daß BC = BACD AD die vier Punkte A, B, C und D gesagt werden, um einen harmonischen Bereich zu bilden. Wenn
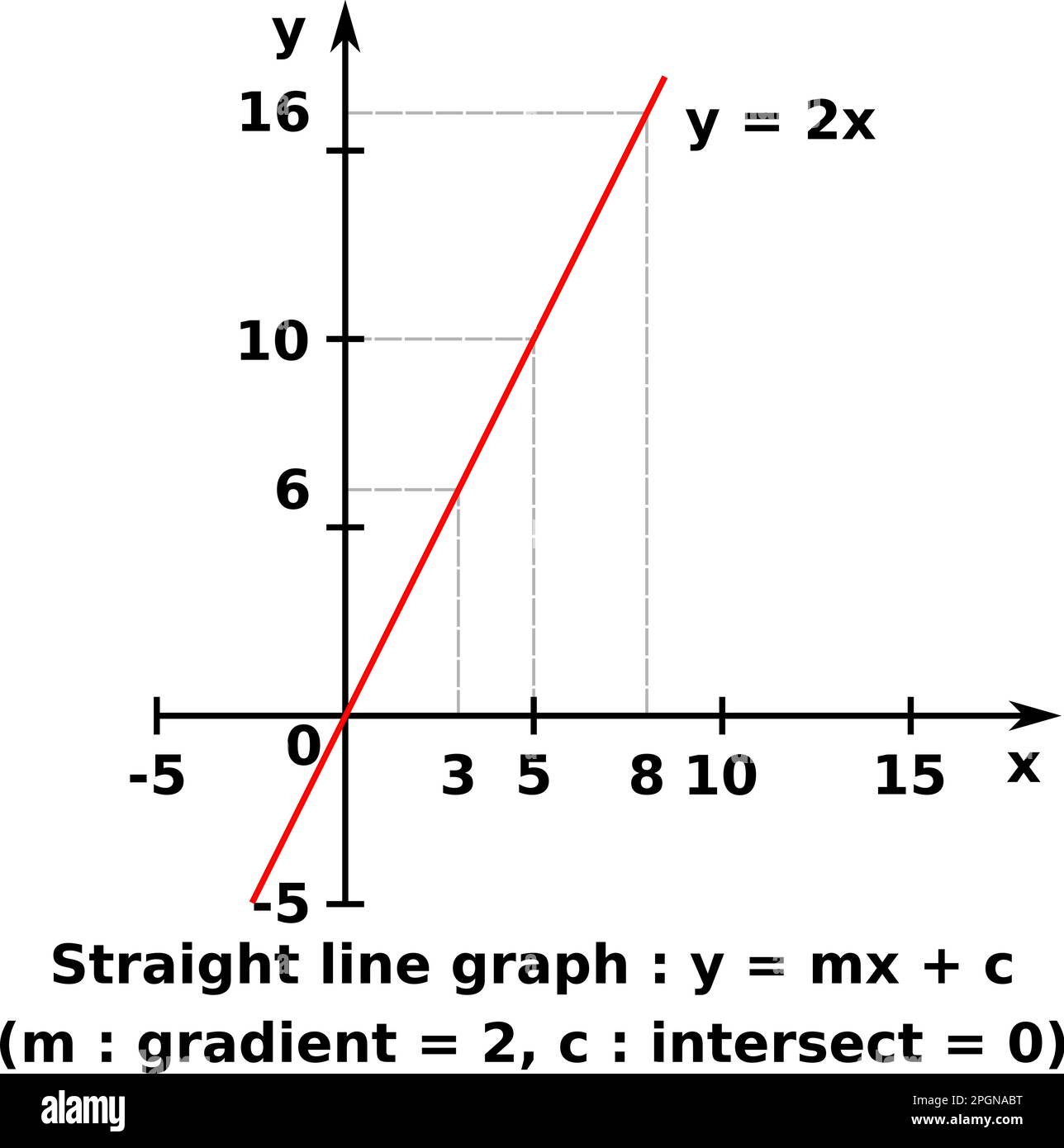 Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = 2x Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektorgrafik-eines-diagramms-von-x-gegen-y-einer-linearen-funktion-die-dargestellte-formel-ist-y-=-2x-image543825068.html
Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = 2x Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/vektorgrafik-eines-diagramms-von-x-gegen-y-einer-linearen-funktion-die-dargestellte-formel-ist-y-=-2x-image543825068.htmlRF2PGNABT–Vektorgrafik eines Diagramms von x gegen y einer linearen Funktion. Die dargestellte Formel ist y = 2x
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96853063.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96853063.htmlRFFHG11Y–Grundlegende Wissenschaft und des Wissens Symbole
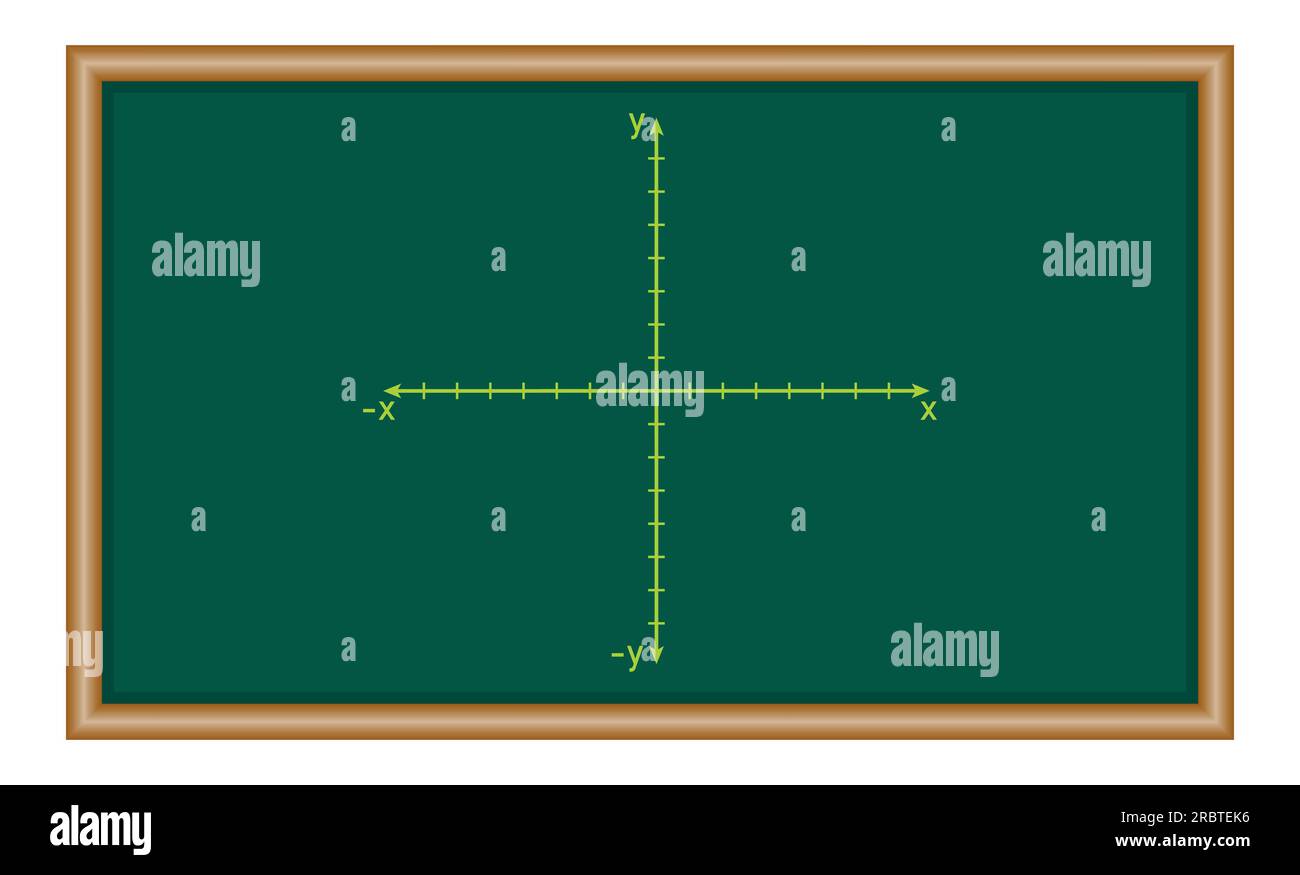 Das kartesische Koordinatensystem in der Ebene. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/das-kartesische-koordinatensystem-in-der-ebene-mathematische-ressourcen-fur-lehrer-und-schuler-image558031354.html
Das kartesische Koordinatensystem in der Ebene. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/das-kartesische-koordinatensystem-in-der-ebene-mathematische-ressourcen-fur-lehrer-und-schuler-image558031354.htmlRF2RBTEK6–Das kartesische Koordinatensystem in der Ebene. Mathematische Ressourcen für Lehrer und Schüler.
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-vektor-image471473028.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-der-systemvorlage-fur-die-achsen-x-und-y-vektor-image471473028.htmlRF2JB1CJC–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit der Systemvorlage für die Achsen X und Y. Vektor
 . Differential- und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. cos A + sin a > Arc PQ > 1. Akkord PQ als Q =P, a = 0, sin a = 0, cos a - 1, und damit Arc PQ (A) q±p Akkord PQ140 = 1. F. E. D. §101 DIE ABLEITUNG DES ARC 141 Sin 11 1, die in Art. nachgewiesen wurde, ist offensichtlich- der Satz lim 0=0 9 ously ein Sonderfall dieses Theorems (a). 101. Die Ableitung des Bogens: Kartesische Koordinaten. Lassen Sie P und Q zwei beliebige Punkte einer Kurve sein, und lassen Sie ihre Koordinatenx, y und x + Axe, y + Ay sein.Lassen Sie s die Länge des arcap sein, gemessen von jedem möglichen con-venient poin Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/differential-und-integralrechnung-ein-einfuhrungskurs-fur-hochschulen-und-ingenieurschulen-cos-a-sin-a-gt-arc-pq-gt-1-akkord-pq-als-q-=p-a-=-0-sin-a-=-0-cos-a-1-und-damit-arc-pq-a-qp-akkord-pq140-=-1-f-e-d-101-die-ableitung-des-arc-141-sin-11-1-die-in-art-nachgewiesen-wurde-ist-offensichtlich-der-satz-lim-0=0-9-ously-ein-sonderfall-dieses-theorems-a-101-die-ableitung-des-bogens-kartesische-koordinaten-lassen-sie-p-und-q-zwei-beliebige-punkte-einer-kurve-sein-und-lassen-sie-ihre-koordinatenx-y-und-x-axe-y-ay-seinlassen-sie-s-die-lange-des-arcap-sein-gemessen-von-jedem-moglichen-con-venient-poin-image370434903.html
. Differential- und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. cos A + sin a > Arc PQ > 1. Akkord PQ als Q =P, a = 0, sin a = 0, cos a - 1, und damit Arc PQ (A) q±p Akkord PQ140 = 1. F. E. D. §101 DIE ABLEITUNG DES ARC 141 Sin 11 1, die in Art. nachgewiesen wurde, ist offensichtlich- der Satz lim 0=0 9 ously ein Sonderfall dieses Theorems (a). 101. Die Ableitung des Bogens: Kartesische Koordinaten. Lassen Sie P und Q zwei beliebige Punkte einer Kurve sein, und lassen Sie ihre Koordinatenx, y und x + Axe, y + Ay sein.Lassen Sie s die Länge des arcap sein, gemessen von jedem möglichen con-venient poin Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/differential-und-integralrechnung-ein-einfuhrungskurs-fur-hochschulen-und-ingenieurschulen-cos-a-sin-a-gt-arc-pq-gt-1-akkord-pq-als-q-=p-a-=-0-sin-a-=-0-cos-a-1-und-damit-arc-pq-a-qp-akkord-pq140-=-1-f-e-d-101-die-ableitung-des-arc-141-sin-11-1-die-in-art-nachgewiesen-wurde-ist-offensichtlich-der-satz-lim-0=0-9-ously-ein-sonderfall-dieses-theorems-a-101-die-ableitung-des-bogens-kartesische-koordinaten-lassen-sie-p-und-q-zwei-beliebige-punkte-einer-kurve-sein-und-lassen-sie-ihre-koordinatenx-y-und-x-axe-y-ay-seinlassen-sie-s-die-lange-des-arcap-sein-gemessen-von-jedem-moglichen-con-venient-poin-image370434903.htmlRM2CEJNDY–. Differential- und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. cos A + sin a > Arc PQ > 1. Akkord PQ als Q =P, a = 0, sin a = 0, cos a - 1, und damit Arc PQ (A) q±p Akkord PQ140 = 1. F. E. D. §101 DIE ABLEITUNG DES ARC 141 Sin 11 1, die in Art. nachgewiesen wurde, ist offensichtlich- der Satz lim 0=0 9 ously ein Sonderfall dieses Theorems (a). 101. Die Ableitung des Bogens: Kartesische Koordinaten. Lassen Sie P und Q zwei beliebige Punkte einer Kurve sein, und lassen Sie ihre Koordinatenx, y und x + Axe, y + Ay sein.Lassen Sie s die Länge des arcap sein, gemessen von jedem möglichen con-venient poin
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96807798.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96807798.htmlRFFHDY9A–Grundlegende Wissenschaft und des Wissens Symbole
 Das kartesische Koordinatensystem in der Ebene. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/das-kartesische-koordinatensystem-in-der-ebene-mathematische-ressourcen-fur-lehrer-und-schuler-image558028988.html
Das kartesische Koordinatensystem in der Ebene. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/das-kartesische-koordinatensystem-in-der-ebene-mathematische-ressourcen-fur-lehrer-und-schuler-image558028988.htmlRF2RBTBJM–Das kartesische Koordinatensystem in der Ebene. Mathematische Ressourcen für Lehrer und Schüler.
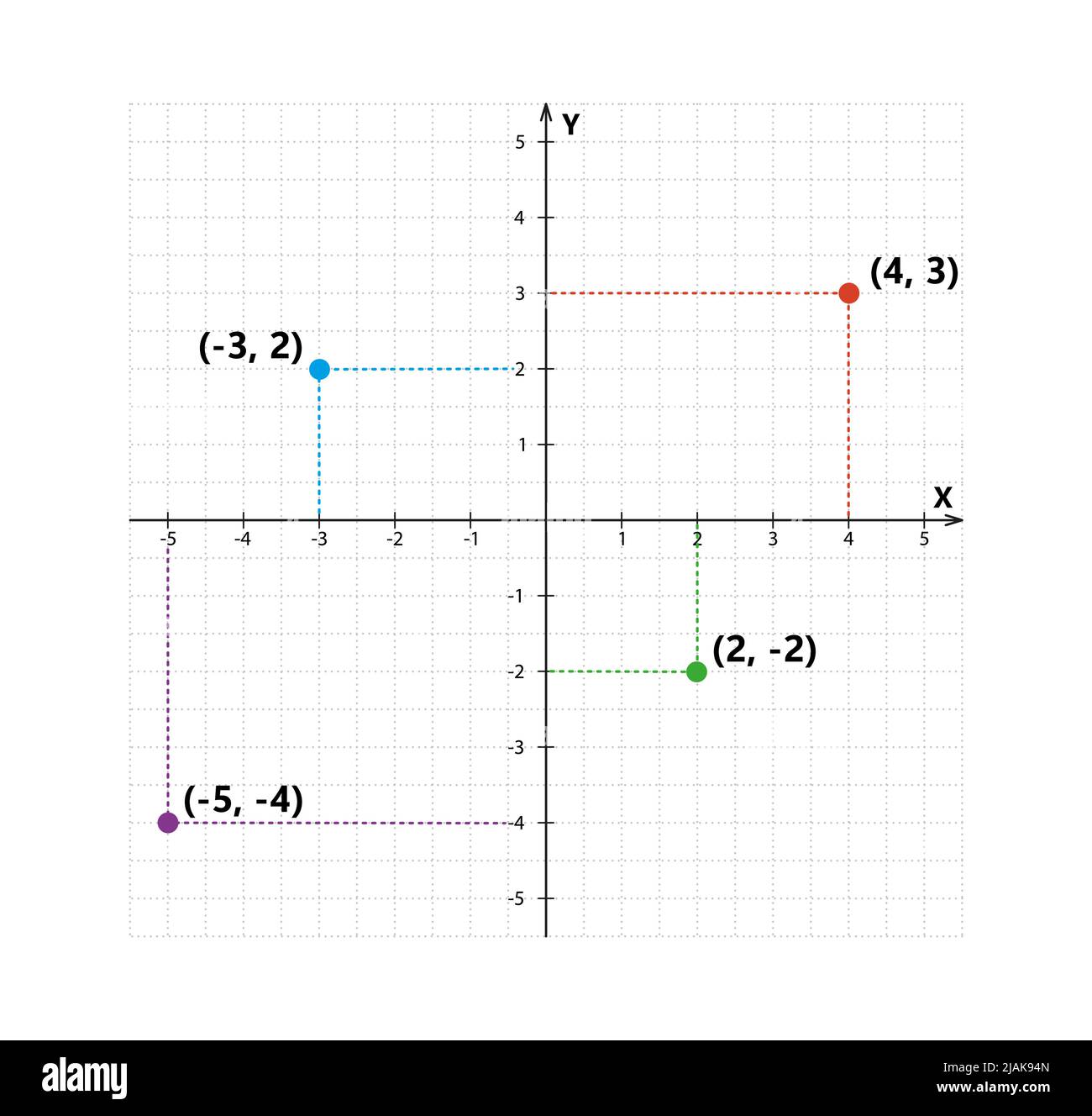 Kartesisches Koordinatensystem in zwei Dimensionen mit Probenpunkten. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-in-zwei-dimensionen-mit-probenpunkten-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vektor-image471250773.html
Kartesisches Koordinatensystem in zwei Dimensionen mit Probenpunkten. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vektor Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kartesisches-koordinatensystem-in-zwei-dimensionen-mit-probenpunkten-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vektor-image471250773.htmlRF2JAK94N–Kartesisches Koordinatensystem in zwei Dimensionen mit Probenpunkten. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vektor
 Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Dann eine einfache representingposition in einer Ebene, die durch algebraische Symbole. Dieses System iscalled die rechteckigen, und ist ein Sonderfall des Cartesiancoordinates. In der Allgemeinen kartesischen System die axesare nicht notwendigerweise senkrecht zueinander. In casethey nicht senkrecht sind, ist das System schräg genannt. Alle obigen Definitionen halten für die obliquesystem. In Abb. 8, NP ist die Abszisse von P und MP wird seinen gewöhnlichen Nate. Während die rechtwinkligen Koordinaten sind häufiger aresimpler usedbecause ihre Formeln, doch wird sie in den Lautspre- s Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/flugzeug-und-solide-analytische-geometrie-eine-elementare-lehrbuch-dann-eine-einfache-representingposition-in-einer-ebene-die-durch-algebraische-symbole-dieses-system-iscalled-die-rechteckigen-und-ist-ein-sonderfall-des-cartesiancoordinates-in-der-allgemeinen-kartesischen-system-die-axesare-nicht-notwendigerweise-senkrecht-zueinander-in-casethey-nicht-senkrecht-sind-ist-das-system-schrag-genannt-alle-obigen-definitionen-halten-fur-die-obliquesystem-in-abb-8-np-ist-die-abszisse-von-p-und-mp-wird-seinen-gewohnlichen-nate-wahrend-die-rechtwinkligen-koordinaten-sind-haufiger-aresimpler-usedbecause-ihre-formeln-doch-wird-sie-in-den-lautspre-s-image338437364.html
Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Dann eine einfache representingposition in einer Ebene, die durch algebraische Symbole. Dieses System iscalled die rechteckigen, und ist ein Sonderfall des Cartesiancoordinates. In der Allgemeinen kartesischen System die axesare nicht notwendigerweise senkrecht zueinander. In casethey nicht senkrecht sind, ist das System schräg genannt. Alle obigen Definitionen halten für die obliquesystem. In Abb. 8, NP ist die Abszisse von P und MP wird seinen gewöhnlichen Nate. Während die rechtwinkligen Koordinaten sind häufiger aresimpler usedbecause ihre Formeln, doch wird sie in den Lautspre- s Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/flugzeug-und-solide-analytische-geometrie-eine-elementare-lehrbuch-dann-eine-einfache-representingposition-in-einer-ebene-die-durch-algebraische-symbole-dieses-system-iscalled-die-rechteckigen-und-ist-ein-sonderfall-des-cartesiancoordinates-in-der-allgemeinen-kartesischen-system-die-axesare-nicht-notwendigerweise-senkrecht-zueinander-in-casethey-nicht-senkrecht-sind-ist-das-system-schrag-genannt-alle-obigen-definitionen-halten-fur-die-obliquesystem-in-abb-8-np-ist-die-abszisse-von-p-und-mp-wird-seinen-gewohnlichen-nate-wahrend-die-rechtwinkligen-koordinaten-sind-haufiger-aresimpler-usedbecause-ihre-formeln-doch-wird-sie-in-den-lautspre-s-image338437364.htmlRM2AJH48M–Flugzeug und solide analytische Geometrie; eine elementare Lehrbuch. Dann eine einfache representingposition in einer Ebene, die durch algebraische Symbole. Dieses System iscalled die rechteckigen, und ist ein Sonderfall des Cartesiancoordinates. In der Allgemeinen kartesischen System die axesare nicht notwendigerweise senkrecht zueinander. In casethey nicht senkrecht sind, ist das System schräg genannt. Alle obigen Definitionen halten für die obliquesystem. In Abb. 8, NP ist die Abszisse von P und MP wird seinen gewöhnlichen Nate. Während die rechtwinkligen Koordinaten sind häufiger aresimpler usedbecause ihre Formeln, doch wird sie in den Lautspre- s
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96839309.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96839309.htmlRFFHFBEN–Grundlegende Wissenschaft und des Wissens Symbole
 Die Punkte in der Koordinatenebene in der Mathematik. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-mathematische-ressourcen-fur-lehrer-und-schuler-image558688341.html
Die Punkte in der Koordinatenebene in der Mathematik. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-mathematische-ressourcen-fur-lehrer-und-schuler-image558688341.htmlRF2RCXCK1–Die Punkte in der Koordinatenebene in der Mathematik. Mathematische Ressourcen für Lehrer und Schüler.
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image473784322.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image473784322.htmlRF2JEPMMJ–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung
 Kansas Universität vierteljährlich. , Ao Bo i k^B, X Y I 0 A B I I B, ich k, A, B, I K, I (6) Wenn wir gehen von Kartesischen homogene Koordinaten, theseforms können geschrieben werden. Px ^ = (7) x y z0 x y z0 A B C A A B C B A, Bj C, K, A, • ziborium = A, B, C, K, B, Ag Bg C, k" A., Ao Bo C2kgBg x y z0 A B C C pZj = A, B, C, K, C, A" B.Co k, C., wodurch die Cs und Zs Einheit und Teilung des ist und 2. der 3., erhalten wir die Gleichungen (6). Das Gesetz der Bildung dieser Determinanten ist offensichtlich. die Determinante der invarianten Dreieck über byX, y grenzt, z, an der Seite von A, k^^, kgA.;, etc. ^2. Typ II; uns Prop Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kansas-universitat-vierteljahrlich-ao-bo-i-kb-x-y-i-0-a-b-i-i-b-ich-k-a-b-i-k-i-6-wenn-wir-gehen-von-kartesischen-homogene-koordinaten-theseforms-konnen-geschrieben-werden-px-=-7-x-y-z0-x-y-z0-a-b-c-a-a-b-c-b-a-bj-c-k-a-ziborium-=-a-b-c-k-b-ag-bg-c-k-a-ao-bo-c2kgbg-x-y-z0-a-b-c-c-pzj-=-a-b-c-k-c-a-bco-k-c-wodurch-die-cs-und-zs-einheit-und-teilung-des-ist-und-2-der-3-erhalten-wir-die-gleichungen-6-das-gesetz-der-bildung-dieser-determinanten-ist-offensichtlich-die-determinante-der-invarianten-dreieck-uber-byx-y-grenzt-z-an-der-seite-von-a-k-kga-etc-2-typ-ii-uns-prop-image339139322.html
Kansas Universität vierteljährlich. , Ao Bo i k^B, X Y I 0 A B I I B, ich k, A, B, I K, I (6) Wenn wir gehen von Kartesischen homogene Koordinaten, theseforms können geschrieben werden. Px ^ = (7) x y z0 x y z0 A B C A A B C B A, Bj C, K, A, • ziborium = A, B, C, K, B, Ag Bg C, k" A., Ao Bo C2kgBg x y z0 A B C C pZj = A, B, C, K, C, A" B.Co k, C., wodurch die Cs und Zs Einheit und Teilung des ist und 2. der 3., erhalten wir die Gleichungen (6). Das Gesetz der Bildung dieser Determinanten ist offensichtlich. die Determinante der invarianten Dreieck über byX, y grenzt, z, an der Seite von A, k^^, kgA.;, etc. ^2. Typ II; uns Prop Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/kansas-universitat-vierteljahrlich-ao-bo-i-kb-x-y-i-0-a-b-i-i-b-ich-k-a-b-i-k-i-6-wenn-wir-gehen-von-kartesischen-homogene-koordinaten-theseforms-konnen-geschrieben-werden-px-=-7-x-y-z0-x-y-z0-a-b-c-a-a-b-c-b-a-bj-c-k-a-ziborium-=-a-b-c-k-b-ag-bg-c-k-a-ao-bo-c2kgbg-x-y-z0-a-b-c-c-pzj-=-a-b-c-k-c-a-bco-k-c-wodurch-die-cs-und-zs-einheit-und-teilung-des-ist-und-2-der-3-erhalten-wir-die-gleichungen-6-das-gesetz-der-bildung-dieser-determinanten-ist-offensichtlich-die-determinante-der-invarianten-dreieck-uber-byx-y-grenzt-z-an-der-seite-von-a-k-kga-etc-2-typ-ii-uns-prop-image339139322.htmlRM2AKN3JJ–Kansas Universität vierteljährlich. , Ao Bo i k^B, X Y I 0 A B I I B, ich k, A, B, I K, I (6) Wenn wir gehen von Kartesischen homogene Koordinaten, theseforms können geschrieben werden. Px ^ = (7) x y z0 x y z0 A B C A A B C B A, Bj C, K, A, • ziborium = A, B, C, K, B, Ag Bg C, k" A., Ao Bo C2kgBg x y z0 A B C C pZj = A, B, C, K, C, A" B.Co k, C., wodurch die Cs und Zs Einheit und Teilung des ist und 2. der 3., erhalten wir die Gleichungen (6). Das Gesetz der Bildung dieser Determinanten ist offensichtlich. die Determinante der invarianten Dreieck über byX, y grenzt, z, an der Seite von A, k^^, kgA.;, etc. ^2. Typ II; uns Prop
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96822162.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96822162.htmlRFFHEHJA–Grundlegende Wissenschaft und des Wissens Symbole
 Die Punkte in der Koordinatenebene in der Mathematik. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-mathematische-ressourcen-fur-lehrer-und-schuler-image558028940.html
Die Punkte in der Koordinatenebene in der Mathematik. Mathematische Ressourcen für Lehrer und Schüler. Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/die-punkte-in-der-koordinatenebene-in-der-mathematik-mathematische-ressourcen-fur-lehrer-und-schuler-image558028940.htmlRF2RBTBH0–Die Punkte in der Koordinatenebene in der Mathematik. Mathematische Ressourcen für Lehrer und Schüler.
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image471854662.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image471854662.htmlRF2JBJRC6–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96831866.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96831866.htmlRFFHF20X–Grundlegende Wissenschaft und des Wissens Symbole
 Konjugieren komplexer Zahlen in der Mathematik. argand-Diagramm Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/konjugieren-komplexer-zahlen-in-der-mathematik-argand-diagramm-image483808101.html
Konjugieren komplexer Zahlen in der Mathematik. argand-Diagramm Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/konjugieren-komplexer-zahlen-in-der-mathematik-argand-diagramm-image483808101.htmlRF2K33A4N–Konjugieren komplexer Zahlen in der Mathematik. argand-Diagramm
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image500689534.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image500689534.htmlRF2M2GAH2–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96827118.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96827118.htmlRFFHERYA–Grundlegende Wissenschaft und des Wissens Symbole
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image470033506.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image470033506.htmlRF2J8KTEX–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96848844.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96848844.htmlRFFHFRK8–Grundlegende Wissenschaft und des Wissens Symbole
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image472389392.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image472389392.htmlRF2JCF5DM–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96812437.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96812437.htmlRFFHE571–Grundlegende Wissenschaft und des Wissens Symbole
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image471152755.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image471152755.htmlRF2JAET43–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96976331.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96976331.htmlRFFHNJ8B–Grundlegende Wissenschaft und des Wissens Symbole
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image485191315.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image485191315.htmlRF2K5AAD7–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung
 Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96864625.html
Grundlegende Wissenschaft und des Wissens Symbole Stockfotohttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/stockfoto-grundlegende-wissenschaft-und-des-wissens-symbole-96864625.htmlRFFHGFPW–Grundlegende Wissenschaft und des Wissens Symbole
 Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image470725337.html
Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung Stock Vektorhttps://www.alamy.de/image-license-details/?v=1https://www.alamy.de/leeres-kartesisches-koordinatensystem-in-zwei-dimensionen-rechteckige-orthogonale-koordinatenebene-mit-achsen-x-und-y-auf-quadratischem-raster-vorlage-fur-mathematische-skalierung-image470725337.htmlRF2J9RAY5–Leeres kartesisches Koordinatensystem in zwei Dimensionen. Rechteckige orthogonale Koordinatenebene mit Achsen X und Y auf quadratischem Raster. Vorlage für mathematische Skalierung
