Dy dx -Fotos und -Bildmaterial in hoher Auflösung - Seite 2

. Differential- und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. S 0, ds ± = smd, (b) dx = cos 8 ds, dy = sin 9 ds. Diese Gleichungen können direkt aus der Abbildung abgeleitet werden, wenn wedenken sie daran, dass die Seiten des Dreiecks PBT DX, dy, ds sind. Problem. III direkt aus dem Dreieck PBQ ableiten. In Art. 84 wurde gezeigt, dass DXY = -=p = tan 0. Dann durch II des vorliegenden ArtikelsDts DXS = Whence IV (A) D,x VL + tan2 0 = s 0, DTX = cos 6 DTS, DTY = tan 6 DTX = sin 0 DTS. rw dx (b) IT nds COS 6 -r, dt dy . Qdsdt Clearing IV (b) von Fraktionen, haben wir einen Beweis dafür, dass III (b) Stockfoto

RM2CEJN8M–. Differential- und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. S 0, ds ± = smd, (b) dx = cos 8 ds, dy = sin 9 ds. Diese Gleichungen können direkt aus der Abbildung abgeleitet werden, wenn wedenken sie daran, dass die Seiten des Dreiecks PBT DX, dy, ds sind. Problem. III direkt aus dem Dreieck PBQ ableiten. In Art. 84 wurde gezeigt, dass DXY = -=p = tan 0. Dann durch II des vorliegenden ArtikelsDts DXS = Whence IV (A) D,x VL + tan2 0 = s 0, DTX = cos 6 DTS, DTY = tan 6 DTX = sin 0 DTS. rw dx (b) IT nds COS 6 -r, dt dy . Qdsdt Clearing IV (b) von Fraktionen, haben wir einen Beweis dafür, dass III (b)

. Differential-und Integralrechnung. Ittedat der Rate von 10 Cu. Ft. Eine Sekunde, mit welcher Rate ist die Pistonmoving ? 62 Differentialrechnung Let y = Volumen und x = Höhe des Zylinders zu einem beliebigen Zeitpunkt;then = »£)V.-. dy = - rtfr,4 40 .*. dx - - Füße eine Sekunde. 7T 6. Gas wird in einen dünnen elastischen Kugelfilm mit einer Länge von 10 Kubikmeter pro Sekunde eingebracht. Mit welcher Rate erhöht sich der Radius, wenn das Volumen in Kubikfuß liegt. ? 3 Let y = Volumen und x variabler Radius ; dann y = -ttxs, .. dy = 4 7rx2dx,3 dx 43dy 10 1 4 TTX2 4OO 7T 40 7T Fuß pro Sekunde. 7. Ein Mann 6 Fuß in der Höhe, zu Fuß in der Geschwindigkeit von 2 Milesa Stockfoto

RM2CEPG48–. Differential-und Integralrechnung. Ittedat der Rate von 10 Cu. Ft. Eine Sekunde, mit welcher Rate ist die Pistonmoving ? 62 Differentialrechnung Let y = Volumen und x = Höhe des Zylinders zu einem beliebigen Zeitpunkt;then = »£)V.-. dy = - rtfr,4 40 .*. dx - - Füße eine Sekunde. 7T 6. Gas wird in einen dünnen elastischen Kugelfilm mit einer Länge von 10 Kubikmeter pro Sekunde eingebracht. Mit welcher Rate erhöht sich der Radius, wenn das Volumen in Kubikfuß liegt. ? 3 Let y = Volumen und x variabler Radius ; dann y = -ttxs, .. dy = 4 7rx2dx,3 dx 43dy 10 1 4 TTX2 4OO 7T 40 7T Fuß pro Sekunde. 7. Ein Mann 6 Fuß in der Höhe, zu Fuß in der Geschwindigkeit von 2 Milesa

. Differential- und Integralrechnung. dx y. â â¢>X X,= Â£A) dy 2 yas seit 2y = Akkord AC sehen wir dieSchwerpunkteeines kreisförmigen Kreisbogens auf seinem Symmetrieradius und an der Höhe von seinem Zentrum gleich dem vierten Proportionalverhältnis zwischen Bogen, Radius und Akkord. 244. 7b findet den Schwerpunkt eines kreisförmigen Segments.Hier dv = D2A = dxdy; daher rx: 4 n xdxdy V*2 ** VÂ«Â«=P xdxdy 381 Mechanische Anwendungen2 j V#2 â x?xdx JX A -f(^2-^A = %(a*-*y A ira2Wenn der Sektor ein Halbkreis ist, dann A = â und # = o. 2 *, = 40 3^ 245. Um den Schwerpunkt des von apa begrenzten Bereichs zu ermitteln Stockfoto

RM2CEPCYN–. Differential- und Integralrechnung. dx y. â â¢>X X,= Â£A) dy 2 yas seit 2y = Akkord AC sehen wir dieSchwerpunkteeines kreisförmigen Kreisbogens auf seinem Symmetrieradius und an der Höhe von seinem Zentrum gleich dem vierten Proportionalverhältnis zwischen Bogen, Radius und Akkord. 244. 7b findet den Schwerpunkt eines kreisförmigen Segments.Hier dv = D2A = dxdy; daher rx: 4 n xdxdy V*2 ** VÂ«Â«=P xdxdy 381 Mechanische Anwendungen2 j V#2 â x?xdx JX A -f(^2-^A = %(a*-*y A ira2Wenn der Sektor ein Halbkreis ist, dann A = â und # = o. 2 *, = 40 3^ 245. Um den Schwerpunkt des von apa begrenzten Bereichs zu ermitteln

. Differential- und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. En(a) (1) a = Vai2 + a22, (2) <*i = a cos 0, a2 = a sin 0. 106. Auflösung der Geschwindigkeit entlang einer Kurve. Nehmen wir an, ein Körper, der sich entlang einer Kurve bewegt, sei an der Stelle P zum Zeitpunkt t ds (siehe erste Abbildung des Art. 103). Seine tangentiale Geschwindigkeit bei P ist -j, und dx dvits Geschwindigkeiten in Richtung der Achsen sind -r: Und -. Jetzt von dt dt J formuhe II und IV des Art. 101, <b) (1) it=V [it) +UJ (2) ^ -cos ^- ^=s,n • *• beim Vergleich dieser Gleichungen mit (a) oben scheint es, dass -r. dy ds und -j: Sind Stockfoto

RM2CEJM0D–. Differential- und Integralrechnung, ein Einführungskurs für Hochschulen und Ingenieurschulen. En(a) (1) a = Vai2 + a22, (2) <*i = a cos 0, a2 = a sin 0. 106. Auflösung der Geschwindigkeit entlang einer Kurve. Nehmen wir an, ein Körper, der sich entlang einer Kurve bewegt, sei an der Stelle P zum Zeitpunkt t ds (siehe erste Abbildung des Art. 103). Seine tangentiale Geschwindigkeit bei P ist -j, und dx dvits Geschwindigkeiten in Richtung der Achsen sind -r: Und -. Jetzt von dt dt J formuhe II und IV des Art. 101, <b) (1) it=V [it) +UJ (2) ^ -cos ^- ^=s,n • *• beim Vergleich dieser Gleichungen mit (a) oben scheint es, dass -r. dy ds und -j: Sind

. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung. Er Umwandlung oi rechteckig in polare Koordinaten, 276 DIFFERENTIALRECHNUNG. Wir haben x z=zr cos. d^ y ^^r sin. d. Wir haben auch (Kunst. 42,161) ds ds dx dx I (DYV I /(ia^■^ fdy^ do dx do dx dd ^ dx dr . dy . dr aber -- =: COS. d- r SM. (9, –- == SM. d –---r cos.6; dd do dd do^ daher ds dd =J r^ + (-- ) : und, in ähnlicher Weise, ds dd dddr^ dd ds dr dd dr N c?ryCor. Wenn § der Winkel ist, der zwischen dem Radiusvektor einer Kurve am Punkt (r, d) und der Tangentiallinie an diesem ddpoint enthalten ist, haben wir (Art Stockfoto

RM2CHC5WN–. Eine neue Abhandlung über die Elemente der Differential-und Integralrechnung. Er Umwandlung oi rechteckig in polare Koordinaten, 276 DIFFERENTIALRECHNUNG. Wir haben x z=zr cos. d^ y ^^r sin. d. Wir haben auch (Kunst. 42,161) ds ds dx dx I (DYV I /(ia^■^ fdy^ do dx do dx dd ^ dx dr . dy . dr aber -- =: COS. d- r SM. (9, –- == SM. d –---r cos.6; dd do dd do^ daher ds dd =J r^ + (-- ) : und, in ähnlicher Weise, ds dd dddr^ dd ds dr dd dr N c?ryCor. Wenn § der Winkel ist, der zwischen dem Radiusvektor einer Kurve am Punkt (r, d) und der Tangentiallinie an diesem ddpoint enthalten ist, haben wir (Art

$. Eine Abhandlung über die mathematische Theorie der Elastizität . Ansätze der Nulltraktionüber eine Grenze sind cos (x, V) .-^ - cos {y, V) 5 –^ =0, - cos ix, V) ,-^ -H cos(w, V) ^ = 0,6y^ dxdy cxdy ^ da? Und diese sind die gleichen wie OH oy) ds dxj, wobei ds ein Element der Grenze bezeichnet. Daher cj^iox und d^/^y areconstant entlang der Grenze, und wir haben ds^ drJ DSV dx von J ds dx ds dy * Siehe den Satz (ii) des Artikels 59. ANGEWENDET AUF DIE PLANDEHNUNG 215 154, 155] daraus folgt, dass eine von der Traktion freie Grenze im (r, 6) System in eine Grenze transformiert wird, die einer normalen Spannung im (r, 0) sy unterliegt Stockfoto$

RM2CDFD94–. Eine Abhandlung über die mathematische Theorie der Elastizität . Ansätze der Nulltraktionüber eine Grenze sind cos (x, V) .-^ - cos {y, V) 5 –^ =0, - cos ix, V) ,-^ -H cos(w, V) ^ = 0,6y^ dxdy cxdy ^ da? Und diese sind die gleichen wie OH oy) ds dxj, wobei ds ein Element der Grenze bezeichnet. Daher cj^iox und d^/^y areconstant entlang der Grenze, und wir haben ds^ drJ DSV dx von J ds dx ds dy * Siehe den Satz (ii) des Artikels 59. ANGEWENDET AUF DIE PLANDEHNUNG 215 154, 155] daraus folgt, dass eine von der Traktion freie Grenze im (r, 6) System in eine Grenze transformiert wird, die einer normalen Spannung im (r, 0) sy unterliegt

. The Bell System Technical Journal . die Gleichungen d^ dtf d^ d^ drj d^ dy dz dz dx dy Daher kann die relative Verschiebung von zwei beliebigen j.oints ausgedrückt werden asch = XS, + y [-^) + z [-^) (17) (18) 86 GLOCKE SYSTEM TECIINICA L JOI UNA L, die die allgemeinste Art von disj^Lacement, die die HNE P Qcan durchlaufen darstellt. Wie in Abschnitt 4 erläutert, erlaubt die Definition der Scherstämme durch Gleichung (16) nicht, dass sie als Teil eines Tensors dargestellt werden.Wenn wir jedoch die Scherstämme als 25,3 = S, = dy dzj 25 - Si, = i^ + ^i • dz dx 25 definieren. = S. = p + JDX ay (19) Sie können Stockfoto

RM2CRWX4R–. The Bell System Technical Journal . die Gleichungen d^ dtf d^ d^ drj d^ dy dz dz dx dy Daher kann die relative Verschiebung von zwei beliebigen j.oints ausgedrückt werden asch = XS, + y [-^) + z [-^) (17) (18) 86 GLOCKE SYSTEM TECIINICA L JOI UNA L, die die allgemeinste Art von disj^Lacement, die die HNE P Qcan durchlaufen darstellt. Wie in Abschnitt 4 erläutert, erlaubt die Definition der Scherstämme durch Gleichung (16) nicht, dass sie als Teil eines Tensors dargestellt werden.Wenn wir jedoch die Scherstämme als 25,3 = S, = dy dzj 25 - Si, = i^ + ^i • dz dx 25 definieren. = S. = p + JDX ay (19) Sie können

$. Die Bell System technische Zeitschrift . Abb. 1. - Würfel zeigt Methode für die Angabe von Spannungen. Die resultierende Kraft in X-Richtung wird durch Summieren aller Kräfte mit Komponenten in X-Richtung oder F = (n., - r„J dydz + {T^y, - T.y,) dxdz + (n„ - T^,) dxdy ermittelt. (3) aber Tzxt – Txx^ 4 –^ – dx; iiyj – J xyj + I^.,r. r„.= -r„,+^v. (4) und Gleichung (3) können in der Form /dTxx , dTxv 1 DT; J l-^ + -- j^^ + -±^^dxdydz. dx dy dz ) (5) ähnlich wie die resultierenden Kräfte in den anderen Richtungen sind (6) PIEZOELEKTRISCHE KRISTALLE IN TENSOR-FORM 83 Wir nennen die Komponenten r T. T T21, 7^22, T,,T31 , TZ Stockfoto$

RM2CRWX3N–. Die Bell System technische Zeitschrift . Abb. 1. - Würfel zeigt Methode für die Angabe von Spannungen. Die resultierende Kraft in X-Richtung wird durch Summieren aller Kräfte mit Komponenten in X-Richtung oder F = (n., - r„J dydz + {T^y, - T.y,) dxdz + (n„ - T^,) dxdy ermittelt. (3) aber Tzxt – Txx^ 4 –^ – dx; iiyj – J xyj + I^.,r. r„.= -r„,+^v. (4) und Gleichung (3) können in der Form /dTxx , dTxv 1 DT; J l-^ + -- j^^ + -±^^dxdydz. dx dy dz ) (5) ähnlich wie die resultierenden Kräfte in den anderen Richtungen sind (6) PIEZOELEKTRISCHE KRISTALLE IN TENSOR-FORM 83 Wir nennen die Komponenten r T. T T21, 7^22, T,,T31 , TZ

$. Angewandte Kalkül; Grundsätze und Anwendungen . 14. f ^ C^ V2^ dxdy = l V2g {h^ - hx^) b.Jo J Hi Jo J A(l – COS0) o 16. r C {lo ■-2v)dvdw= -W- a. 17. r^ r f^^aj^ ^2 dx dy dz = 32 A, j ./O •0 »/2y 164. Ebenen Flächen durch Doppelintegration – Rechteckkoordinaten. - Es wurde in Art gezeigt, 135, dass der Bereich zwischen zwei Kurven y = f(x) und y = F (x) durch A= rf{x)-F{x)) dx, (1) wo die Schnittpunkte sind (xq, 2/0) und {xi, yi). Das ist also nicht durch ein einzelnes Integral, sondern durch die differe-between zwei Integrale, / f{x)dx - F (x) dx. Das Ergebnis wird auch durch doppelte Integr Stockfoto$

RM2CGGHK1–. Angewandte Kalkül; Grundsätze und Anwendungen . 14. f ^ C^ V2^ dxdy = l V2g {h^ - hx^) b.Jo J Hi Jo J A(l – COS0) o 16. r C {lo ■-2v)dvdw= -W- a. 17. r^ r f^^aj^ ^2 dx dy dz = 32 A, j ./O •0 »/2y 164. Ebenen Flächen durch Doppelintegration – Rechteckkoordinaten. - Es wurde in Art gezeigt, 135, dass der Bereich zwischen zwei Kurven y = f(x) und y = F (x) durch A= rf{x)-F{x)) dx, (1) wo die Schnittpunkte sind (xq, 2/0) und {xi, yi). Das ist also nicht durch ein einzelnes Integral, sondern durch die differe-between zwei Integrale, / f{x)dx - F (x) dx. Das Ergebnis wird auch durch doppelte Integr

. Eine elementare Abhandlung über die Differential-und Integralrechnung. A). 38. Y = cosec-1 als zu unterscheiden. Wir haben a; = cosec y ; daher DX = – cosec# cot?/ <7y = – cosec ?/ Vcosec2 y – 1 dy = – xVx2 – 1 d#. dx dy = = d (cosec-1 a;). ^V z2 – 1 48 BEISPIELE. 39. Y = vers-1 x zu unterscheiden. Wir haben x = vers ^; daher DX = sin y dy = VL – cos2 y dy = VL – (1 – vers y)2 dy= V% vers y – vers2 y dy = V%% – #2 6?y. .*. rfy = -? = E? (Vers-1 x) V2X – x2 40. Zu unterscheiden y = deckt-1 x. Wir haben x = Abdeckungen y; daher DX = – gemütlich dy = – /l – sin2?/ dy = – vl – (1 – Abdeckungen yf dy = – Stockfoto

RM2CEDMC9–. Eine elementare Abhandlung über die Differential-und Integralrechnung. A). 38. Y = cosec-1 als zu unterscheiden. Wir haben a; = cosec y ; daher DX = – cosec# cot?/ <7y = – cosec ?/ Vcosec2 y – 1 dy = – xVx2 – 1 d#. dx dy = = d (cosec-1 a;). ^V z2 – 1 48 BEISPIELE. 39. Y = vers-1 x zu unterscheiden. Wir haben x = vers ^; daher DX = sin y dy = VL – cos2 y dy = VL – (1 – vers y)2 dy= V% vers y – vers2 y dy = V%% – #2 6?y. .*. rfy = -? = E? (Vers-1 x) V2X – x2 40. Zu unterscheiden y = deckt-1 x. Wir haben x = Abdeckungen y; daher DX = – gemütlich dy = – /l – sin2?/ dy = – vl – (1 – Abdeckungen yf dy = –

$. Angewandte Kalkül; Grundsätze und Anwendungen . AY = Sin {d + Ad) – Sin d ALS ein Ay 2 Sin SM Ad AD2 cos hf) ALS i-cos (^i / + A^^ A^^ als^2 = 1, von Trig.; [(Art 46).As AQ = 0; 66 DIFFERENTIALRECHNUNG de AJ?Ola^J Lim A9=0 2-1 sin-^ 2 j-KF) cos ; /. dy = d sin 6 = cos ungerade.Folge. - d deckt 6 = d{l - sind) = - cos 6 do. Nun lasst a; = cos ^ = sin (S – ^) i dx = dcosd = dsinl^ – dj = cosf^ – djdl^ – d); .*. Dcosd = – sin d dd.corollary. – d vers S = d{l – cos 6) – sin Q dB. Lassen Sie d die Anzahl der Radiane im Winkel NO A, wobei der Winkel akut genommen wird; durch Ge-ometrie, wenn AT und BT sind tan-gent Stockfoto$

RM2CGH8W0–. Angewandte Kalkül; Grundsätze und Anwendungen . AY = Sin {d + Ad) – Sin d ALS ein Ay 2 Sin SM Ad AD2 cos hf) ALS i-cos (^i / + A^^ A^^ als^2 = 1, von Trig.; [(Art 46).As AQ = 0; 66 DIFFERENTIALRECHNUNG de AJ?Ola^J Lim A9=0 2-1 sin-^ 2 j-KF) cos ; /. dy = d sin 6 = cos ungerade.Folge. - d deckt 6 = d{l - sind) = - cos 6 do. Nun lasst a; = cos ^ = sin (S – ^) i dx = dcosd = dsinl^ – dj = cosf^ – djdl^ – d); .*. Dcosd = – sin d dd.corollary. – d vers S = d{l – cos 6) – sin Q dB. Lassen Sie d die Anzahl der Radiane im Winkel NO A, wobei der Winkel akut genommen wird; durch Ge-ometrie, wenn AT und BT sind tan-gent

. Angewandter Kalkül; Prinzipien und Anwendungen . zu OX und dargestellt in der Länge durch NNI, obwohl es nicht das gleiche wie AX = dx ist, aber ist wirklich länger. Beispiel 1. - um die seitliche Oberfläche des Kegels vonArt zu finden. 155: Durch (3), S = 2^ i yds = 2Trl -^ sds, wobei s = -y = OPf n Si-= 2 TT 7 PR = -wal, wobei I = Oph, ein Element. 6 z Jo wieder, J^SFT /•2/=A I /I i yds = 2TR I y-dy, da ds = d(-y]=-dy^0 Jo CT A / ein Grenzwert oder Endwert von I in ein geändert wird Beispiel 2. - die Oberfläche des Paraboloids vonArt zu finden. 156: J^l 1 1 2/ [1 + 64 y^]dy, von 2/^ = 7 x,0 4 .[l + (64,^)i]J = ^ ((65)1-1) 27r1 Stockfoto

RM2CGGMKY–. Angewandter Kalkül; Prinzipien und Anwendungen . zu OX und dargestellt in der Länge durch NNI, obwohl es nicht das gleiche wie AX = dx ist, aber ist wirklich länger. Beispiel 1. - um die seitliche Oberfläche des Kegels vonArt zu finden. 155: Durch (3), S = 2^ i yds = 2Trl -^ sds, wobei s = -y = OPf n Si-= 2 TT 7 PR = -wal, wobei I = Oph, ein Element. 6 z Jo wieder, J^SFT /•2/=A I /I i yds = 2TR I y-dy, da ds = d(-y]=-dy^0 Jo CT A / ein Grenzwert oder Endwert von I in ein geändert wird Beispiel 2. - die Oberfläche des Paraboloids vonArt zu finden. 156: J^l 1 1 2/ [1 + 64 y^]dy, von 2/^ = 7 x,0 4 .[l + (64,^)i]J = ^ ((65)1-1) 27r1

$. Eine Abhandlung über die mathematische Theorie der Elastizität . rdingly dy inAQ B^ = -^ F^dx i oe, - ^Q^ di = dy W i (l-x). 247] AUF EINER SPANNE 379 Wir integrieren diese in die Formen B (?/ - A; tan A) = - ^ Z- FF V,B{y-(l- A;)tan/3] = - i l-W^{l- xf, wobei tana und tan/3 die Abwärtshänge der Mittellinie an den Punkten A und B sind. Die Bedingungen für die Kontinuität von y und dyjdx bei Q sind B ; tan A - ^ Z-i TF f f = Bf tan /3 - ^ Z F^p, B tan A - ^ ?-i TTF f = - B tan JS + i Z TFF^=- Diese Gleichungen geben B tan A = i l-^^ W^ ( + 2r), B tan /3 = J Z-^ Wenn ^f (2? + f )? Daher in J.Q, wobei f > a; > 0, Stockfoto$

RM2CDF1C7–. Eine Abhandlung über die mathematische Theorie der Elastizität . rdingly dy inAQ B^ = -^ F^dx i oe, - ^Q^ di = dy W i (l-x). 247] AUF EINER SPANNE 379 Wir integrieren diese in die Formen B (?/ - A; tan A) = - ^ Z- FF V,B{y-(l- A;)tan/3] = - i l-W^{l- xf, wobei tana und tan/3 die Abwärtshänge der Mittellinie an den Punkten A und B sind. Die Bedingungen für die Kontinuität von y und dyjdx bei Q sind B ; tan A - ^ Z-i TF f f = Bf tan /3 - ^ Z F^p, B tan A - ^ ?-i TTF f = - B tan JS + i Z TFF^=- Diese Gleichungen geben B tan A = i l-^^ W^ ( + 2r), B tan /3 = J Z-^ Wenn ^f (2? + f )? Daher in J.Q, wobei f > a; > 0,

$. Grafische und mechanische Berechnung . 6 o 3 a3 = -{yi- y4) sin 900.3 ^5 = (y2 - yd sin 300 - (yr - y5) sin 6 o 3 61 = (yi + y5) sin 300 + (y2 + y4) sin 60 900.3 + y3 sin ^^3 = (» i - y3 + y 900) sin . 3 h = (ji -f y5) Sin 300 - (y2 + y4) Sin 6o + y3 Sin 900.Wir können die Arbeit bequem in folgender Rechenform anordnen: yi y* yt ^5 y* Sum si S2 S3 Diff. dy d2 prüft: 0 = fli + a3 + AS. ys = h – bz + b6. Multiplikatoren Cosinusbegriffe Sinusbegriffe sin 30 Grad = 0,5sin 60 Grad = 0,866sin 90 Grad = 1.0 d2 dx -d2 Si SiS3 Si SJ Summe der 1. Spalte Summe der 2d Spalte. SumDiff. 3 a!3a6 3 a( 3 613 66 3 6, Ergebnis: Y = A CO Stockfoto$

RM2CDGD21–. Grafische und mechanische Berechnung . 6 o 3 a3 = -{yi- y4) sin 900.3 ^5 = (y2 - yd sin 300 - (yr - y5) sin 6 o 3 61 = (yi + y5) sin 300 + (y2 + y4) sin 60 900.3 + y3 sin ^^3 = (» i - y3 + y 900) sin . 3 h = (ji -f y5) Sin 300 - (y2 + y4) Sin 6o + y3 Sin 900.Wir können die Arbeit bequem in folgender Rechenform anordnen: yi y* yt ^5 y* Sum si S2 S3 Diff. dy d2 prüft: 0 = fli + a3 + AS. ys = h – bz + b6. Multiplikatoren Cosinusbegriffe Sinusbegriffe sin 30 Grad = 0,5sin 60 Grad = 0,866sin 90 Grad = 1.0 d2 dx -d2 Si SiS3 Si SJ Summe der 1. Spalte Summe der 2d Spalte. SumDiff. 3 a!3a6 3 a( 3 613 66 3 6, Ergebnis: Y = A CO

. Gesammelte reprints/Atlantic ozeanographische und meteorologische Laboratorien [und] Pacific ozeanographische Laboratories. Ozeanographie Zeitschriften.. Juli 1975 R. MOLINARI UND A. D. KI R W A N, JR. 487 Zum Beispiel, eine 90°-Drehung im Uhrzeigersinn verwandelt U-*-V] diese Substitution in die divergenz Ausdruck in (5), Es wird gesehen, dass (dV/dX-dU/dY) - + (dU'/dX + dV '/dY). (6) Der rechten Seite von (6) wird als{/A') dA'/dt, wo EIN' ist der Bereich, der durch das Dreieck, dessen Eckpunkte durch den gedrehten Geschwindigkeitsvektoren gebildet werden geschlossene anerkannt. Die Zeit, die Geschwindigkeit von Veränderungen ist, indem die Differenz zwischen Th ausgewertet Stockfoto

RMREHB6M–. Gesammelte reprints/Atlantic ozeanographische und meteorologische Laboratorien [und] Pacific ozeanographische Laboratories. Ozeanographie Zeitschriften.. Juli 1975 R. MOLINARI UND A. D. KI R W A N, JR. 487 Zum Beispiel, eine 90°-Drehung im Uhrzeigersinn verwandelt U-*-V] diese Substitution in die divergenz Ausdruck in (5), Es wird gesehen, dass (dV/dX-dU/dY) - + (dU'/dX + dV '/dY). (6) Der rechten Seite von (6) wird als{/A') dA'/dt, wo EIN' ist der Bereich, der durch das Dreieck, dessen Eckpunkte durch den gedrehten Geschwindigkeitsvektoren gebildet werden geschlossene anerkannt. Die Zeit, die Geschwindigkeit von Veränderungen ist, indem die Differenz zwischen Th ausgewertet

$. Ein Kommentar auf die wissenschaftlichen Schriften von J. Willard Gibbs. Gibbs, Joniah Willard, 1839-1908; Wissenschaft; Thermodynamik. Angespannte elastischen Feststoffen 469 Region wird von s" unterteilt, und diejenigen, die mit dem Suffix2 betroffen für die normale nach außen gerichteten aus dem zweiten Teil. (Natürlich a/'=-ai"^i" =-182", 7 i" = -72".) Auf hinzufügen Ergebnisse für alle Spalten wir das Ergebnis 9^ dx, dx ' dy ' dz'=j a> Ds' + j{a," 4> x + "2".^2) Ds" und zwei ähnliche Ergebnisse durch die Verwendung von Spalten parallel zu den Achsen OY und OZ' abgeleitet werden können. Wenn Überlegungen wie t Stockfoto$

RMREGNK5–. Ein Kommentar auf die wissenschaftlichen Schriften von J. Willard Gibbs. Gibbs, Joniah Willard, 1839-1908; Wissenschaft; Thermodynamik. Angespannte elastischen Feststoffen 469 Region wird von s" unterteilt, und diejenigen, die mit dem Suffix2 betroffen für die normale nach außen gerichteten aus dem zweiten Teil. (Natürlich a/'=-ai"^i" =-182", 7 i" = -72".) Auf hinzufügen Ergebnisse für alle Spalten wir das Ergebnis 9^ dx, dx ' dy ' dz'=j a> Ds' + j{a," 4> x + "2".^2) Ds" und zwei ähnliche Ergebnisse durch die Verwendung von Spalten parallel zu den Achsen OY und OZ' abgeleitet werden können. Wenn Überlegungen wie t

. Der Carnegie Institution in Washington Publikation. Beispiele für SOLENOIDNYJ FELDER. 41 (c) Dx dy Dz ax b az jeder der drei Gleichungen, die in diesem System enthaltenen Integration, wir v'x = eb xz=c2 z = e b Die Oberflächen für gleiche skalare Werte A des Vektors, der durch die Gleichung (e) A3 = Al+ Al+ Al = 62+a2 (. r'+3' sind), die für jede Konstante Wert eines eine kreisförmige Zylinder um die Achse von y. Die zweite Gleichung (d) zeigt, dass die Positionen der Strömung im Raum Projekt selbst als gleichseitiges Hyperbeln auf der Ebene der Xz. Die zylindrischen Flächen gleicher Intensität schnitt dieses gleichen Pla Stockfoto

RMRFRRR5–. Der Carnegie Institution in Washington Publikation. Beispiele für SOLENOIDNYJ FELDER. 41 (c) Dx dy Dz ax b az jeder der drei Gleichungen, die in diesem System enthaltenen Integration, wir v'x = eb xz=c2 z = e b Die Oberflächen für gleiche skalare Werte A des Vektors, der durch die Gleichung (e) A3 = Al+ Al+ Al = 62+a2 (. r'+3' sind), die für jede Konstante Wert eines eine kreisförmige Zylinder um die Achse von y. Die zweite Gleichung (d) zeigt, dass die Positionen der Strömung im Raum Projekt selbst als gleichseitiges Hyperbeln auf der Ebene der Xz. Die zylindrischen Flächen gleicher Intensität schnitt dieses gleichen Pla

. Die biologische Bulletin. Biologie; Zoologie; Biologie; Meeresbiologie. Funktion der COLUMELLAR FALTEN Anlage Messen True Fläche und Lage auf einer Schale aus einer Reihe von Fotografien 365 Messung der Fläche ein Foto einer XF-Flugzeug, das enthält ein Objekt (Anhang Abb. definiert. 1. A), und die Pixel im Objekt werden" auf, "in der Erwägung, dass jene außerhalb des Objekts "aus." Das Objekt ist eine Projektion einer Oberfläche, Z, auf den XT-Ebene. Die projizierte Fläche, SAZ, ist definiert als SA 7 = dx dy dzV dxdy (AD (Gleichung 6 Eine in Thomas und Finney, 1984). Weil ein digital Pho Stockfoto

RMRHM5DM–. Die biologische Bulletin. Biologie; Zoologie; Biologie; Meeresbiologie. Funktion der COLUMELLAR FALTEN Anlage Messen True Fläche und Lage auf einer Schale aus einer Reihe von Fotografien 365 Messung der Fläche ein Foto einer XF-Flugzeug, das enthält ein Objekt (Anhang Abb. definiert. 1. A), und die Pixel im Objekt werden" auf, "in der Erwägung, dass jene außerhalb des Objekts "aus." Das Objekt ist eine Projektion einer Oberfläche, Z, auf den XT-Ebene. Die projizierte Fläche, SAZ, ist definiert als SA 7 = dx dy dzV dxdy (AD (Gleichung 6 Eine in Thomas und Finney, 1984). Weil ein digital Pho

. Commentarii Academiae Scientiarum Imperialis Petropolitanae. DE IKTEGRAT. AEQVAT. BIFFER. 167^ dx-i-^^ dy dx''^-^^ xdxdy Ddx-^-^ xdx^ Dy - "K72 ziz - 2 ADX-zBxdxdy" "Ddx - 2 Bxdx^ dy"^^ iK, quare Arr-^, dx veladdita coaftanti n. / ^ xxdy ffdxi = (^?? xxdj"^^-Dx - Dy ' ^): xxdy j^^. Videantur ad hcEc duo poftrema exempla, Memoiren^ de rAcad. RoyaJe des Sciemes 1710. ca. finem. DE LNTTEGRATIONIBVS AEQVA - TIONVM DIFFERENTIALIVM, Ubi traditur ARTISTEN ALICVIVS SPEQMEN INTEGRANDI fin^ prasvia feparatione indeterminatariUB: Auctore Joh. BernouUi-L Uando sequatio aliqua difTerentiaris primi^ Stockfoto

RMREG06X–. Commentarii Academiae Scientiarum Imperialis Petropolitanae. DE IKTEGRAT. AEQVAT. BIFFER. 167^ dx-i-^^ dy dx''^-^^ xdxdy Ddx-^-^ xdx^ Dy - "K72 ziz - 2 ADX-zBxdxdy" "Ddx - 2 Bxdx^ dy"^^ iK, quare Arr-^, dx veladdita coaftanti n. / ^ xxdy ffdxi = (^?? xxdj"^^-Dx - Dy ' ^): xxdy j^^. Videantur ad hcEc duo poftrema exempla, Memoiren^ de rAcad. RoyaJe des Sciemes 1710. ca. finem. DE LNTTEGRATIONIBVS AEQVA - TIONVM DIFFERENTIALIVM, Ubi traditur ARTISTEN ALICVIVS SPEQMEN INTEGRANDI fin^ prasvia feparatione indeterminatariUB: Auctore Joh. BernouUi-L Uando sequatio aliqua difTerentiaris primi^

RMREGTEJ–. Gesammelte reprints/Atlantic ozeanographische und meteorologische Laboratorien [und] Pacific ozeanographische Laboratories. Ozeanographie Zeitschriften.. 60 GEZEITENSTRÖMUNGEN. Babybett 10 E UNES 40° 33° 30° 70° Abb. 7. Theoretische corange Chart jor die M: semidaily Tide aus der L'. S. Ostküste. Reichweiten sind in Fuß. Von Redfield (1958). Abb. 6; Die corange und cotidal Charts sind in den Abbildungen. 7. und 8. In Regionen, in denen unten Stress vernachlässigt werden können, die Bewegung wird etwa durch die folgenden Gleichungen: Du-fo=g dt bv dt Dr, dt^1 dx +/" =g Dr, dy=-h/du dv dx + dy) (10) (ID (12) Die se

. Bulletin - United States National Museum. Wissenschaft. -01 - 0. ? 13-' "0/10.71 21.43 32.14 DX DY 2.1429 0.5102 ALPHA 14 * AA 02 07 03 08 10 05 12 BB CC ICH DENT VERDINGLICHUNG 42,86 53,57 64,29 75.00. Bitte beachten Sie, dass diese Bilder sind von der gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Aussehen dieser Abbildungen können nicht perfekt dem Original ähneln. extrahiert. United States National Museum, Smithsonian Institution, Usa. Abt. des Innenraums. Washington: Smithsonian Institution Press, [etc. ]; Für Verkauf durch die Supp. von Docs. , U Stockfoto

RMRG7B3P–. Bulletin - United States National Museum. Wissenschaft. -01 - 0. ? 13-' "0/10.71 21.43 32.14 DX DY 2.1429 0.5102 ALPHA 14 * AA 02 07 03 08 10 05 12 BB CC ICH DENT VERDINGLICHUNG 42,86 53,57 64,29 75.00. Bitte beachten Sie, dass diese Bilder sind von der gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Aussehen dieser Abbildungen können nicht perfekt dem Original ähneln. extrahiert. United States National Museum, Smithsonian Institution, Usa. Abt. des Innenraums. Washington: Smithsonian Institution Press, [etc. ]; Für Verkauf durch die Supp. von Docs. , U

. Biologische atlas: ein Leitfaden für die praktische Untersuchung von Pflanzen und Tieren. Natural History. Genießbare FE, OG (Rana esculenta) TLATE XVIII. Fi^. I.E.-riend^ dy Frosch (ior^ suL Ojsptct Fid. 2. DisstctLaru/ram der ventralen suU/MclU J Dx^ii ^. LiJrihSy Fi 6. 3 - LoryUzLdinaX vgrltcal etction, wUJt ihx juxrts festgelegt. heraus. (Fem ^J^") aed iruoAnt BristU Da^^ ruTr& aus af Po^^ tutt riosfril v, SriJu pasetici £ durch lympanLC cnxiLy sr'ic/xCijJ upertuTe,. Bitte beachten Sie, dass diese Bilder aus gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Erscheinungsbild extrahiert werden Stockfoto

RMRHRBGE–. Biologische atlas: ein Leitfaden für die praktische Untersuchung von Pflanzen und Tieren. Natural History. Genießbare FE, OG (Rana esculenta) TLATE XVIII. Fi^. I.E.-riend^ dy Frosch (ior^ suL Ojsptct Fid. 2. DisstctLaru/ram der ventralen suU/MclU J Dx^ii ^. LiJrihSy Fi 6. 3 - LoryUzLdinaX vgrltcal etction, wUJt ihx juxrts festgelegt. heraus. (Fem ^J^") aed iruoAnt BristU Da^^ ruTr& aus af Po^^ tutt riosfril v, SriJu pasetici £ durch lympanLC cnxiLy sr'ic/xCijJ upertuTe,. Bitte beachten Sie, dass diese Bilder aus gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Erscheinungsbild extrahiert werden

. Bulletin - United States National Museum. Wissenschaft. Zwei FORTRAN-II-PROGRAMME FÜR DIE ANALYSE VON MORPHOMETRIE DATEN 53 Grundstück für 12 Proben AEQUIPECTEN KERN - MIAMI UND SEE WERT, Fla., MCZ 197942, 232557, 232553 - Wohn Grundstück Nr. 43 ANMELDEN LO/LOG BIN ALPHA IDENTIFIZIERUNG l"* l*. II 14* AA 01 04 06 BB 05 08 CC 03 10 -0,51. -1,00 * 13 1.00 -0.59 -0. lt DX DY 0.0821 0.0493 -0,23 0,64 1., 05. Bitte beachten Sie, dass diese Bilder aus gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Aussehen dieser Abbildungen können nicht Perfekt ähneln den oder extrahiert werden Stockfoto

RMRG7B3C–. Bulletin - United States National Museum. Wissenschaft. Zwei FORTRAN-II-PROGRAMME FÜR DIE ANALYSE VON MORPHOMETRIE DATEN 53 Grundstück für 12 Proben AEQUIPECTEN KERN - MIAMI UND SEE WERT, Fla., MCZ 197942, 232557, 232553 - Wohn Grundstück Nr. 43 ANMELDEN LO/LOG BIN ALPHA IDENTIFIZIERUNG l"* l*. II 14* AA 01 04 06 BB 05 08 CC 03 10 -0,51. -1,00 * 13 1.00 -0.59 -0. lt DX DY 0.0821 0.0493 -0,23 0,64 1., 05. Bitte beachten Sie, dass diese Bilder aus gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Aussehen dieser Abbildungen können nicht Perfekt ähneln den oder extrahiert werden

. Bulletin international de l'Acadmie des sciences de Cracovie, Classe des Sciences mathmatiques et Naturelles. Wissenschaft; Naturgeschichte; Natural History - - Polen. + 3 u V r r-i J dy '^y' ++ Clu 9 9 z'5? Dx ' dy ' dz'en d^signant par r et r^Ics Entfernungen des Punkte ein et A^au point Nous avons: + 9 h cZ dx ' dy ' dz". dx ' dy ' dz'. Bitte beachten Sie, dass diese Bilder sind von der gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Aussehen dieser Abbildungen können nicht perfekt dem Original ähneln. extrahiert. Akademja Umiejetnoþsci w Krakowie. Wydzial Matem Stockfoto

RMRGNGCX–. Bulletin international de l'Acadmie des sciences de Cracovie, Classe des Sciences mathmatiques et Naturelles. Wissenschaft; Naturgeschichte; Natural History - - Polen. + 3 u V r r-i J dy '^y' ++ Clu 9 9 z'5? Dx ' dy ' dz'en d^signant par r et r^Ics Entfernungen des Punkte ein et A^au point Nous avons: + 9 h cZ dx ' dy ' dz". dx ' dy ' dz'. Bitte beachten Sie, dass diese Bilder sind von der gescannten Seite Bilder, die digital für die Lesbarkeit verbessert haben mögen - Färbung und Aussehen dieser Abbildungen können nicht perfekt dem Original ähneln. extrahiert. Akademja Umiejetnoþsci w Krakowie. Wydzial Matem

$. Acta Societatis Scientiarum Fennicae. Wissenschaft. Stabilität des Oleichgewichtes eines Punktes. 4. Wir behandeln jetzt zuerst den Fallen des Gleichgewichtes in einer ebenen Kurve, in deren Ebene sterben reaultirende äussere Kraft Novalja ist. Die Gleichung der Kurve sei (23) F{x, y) = 0. Mit der in Gl. (23) enthaltenen Bedingung soll sterben Kräftefunction U{x.y) zu einem maximalen gemacht werden. Mit Anwendung eines unbestimmten Multiplikatoren ein ist-auch (24) und (25) Folglich ÖU ^ ^ ÖF ÖF ÖU Ax Ax Oy oy dU^^ öF dU dF öx "öy dx ' dy ' This Gleichung enthält sterben Ortogonalitätsbedingung der Kraft und Kurve Stockfoto$

RMRR3R8A–. Acta Societatis Scientiarum Fennicae. Wissenschaft. Stabilität des Oleichgewichtes eines Punktes. 4. Wir behandeln jetzt zuerst den Fallen des Gleichgewichtes in einer ebenen Kurve, in deren Ebene sterben reaultirende äussere Kraft Novalja ist. Die Gleichung der Kurve sei (23) F{x, y) = 0. Mit der in Gl. (23) enthaltenen Bedingung soll sterben Kräftefunction U{x.y) zu einem maximalen gemacht werden. Mit Anwendung eines unbestimmten Multiplikatoren ein ist-auch (24) und (25) Folglich ÖU ^ ^ ÖF ÖF ÖU Ax Ax Oy oy dU^^ öF dU dF öx "öy dx ' dy ' This Gleichung enthält sterben Ortogonalitätsbedingung der Kraft und Kurve

$. Acta Societatis Scientiarum Fennicae. Wissenschaft. 24 Hj. Hohe q besuchen. (160) Dx ik "ii"-ii "k") (Fi' (è, - V>)+> - 'r^.) d^Ti'a,-- ^) + rr,^ (n,,,,. ,,, X3 dt" dy Hieraus berechnet sich alsdann die kinetische Energie und das Energie-Integral (162); m | (?.,.-^) + '?. J+A)^.^^.^^ (^)+m | ^. + - ^^;;;;;;;;==, ^}=?^ worin Li'mittelst (159) tf ausgedrückt zu denken ist. Für den Druck N und die tangentiale Gegenkraft P Christmas sterben Formeln (27) und (28) hier mit Beachten des Zeichens von q,. N = mg - + mg, w"-mRw-cos (JV,/.')+ mTitsm {N, R) (163) P = mg mBoo ^s bin, ß) - mßf Stockfoto$

RMRR3755–. Acta Societatis Scientiarum Fennicae. Wissenschaft. 24 Hj. Hohe q besuchen. (160) Dx ik "ii"-ii "k") (Fi' (è, - V>)+> - 'r^.) d^Ti'a,-- ^) + rr,^ (n,,,,. ,,, X3 dt" dy Hieraus berechnet sich alsdann die kinetische Energie und das Energie-Integral (162); m | (?.,.-^) + '?. J+A)^.^^.^^ (^)+m | ^. + - ^^;;;;;;;;==, ^}=?^ worin Li'mittelst (159) tf ausgedrückt zu denken ist. Für den Druck N und die tangentiale Gegenkraft P Christmas sterben Formeln (27) und (28) hier mit Beachten des Zeichens von q,. N = mg - + mg, w"-mRw-cos (JV,/.')+ mTitsm {N, R) (163) P = mg mBoo ^s bin, ß) - mßf

$. Bulletin de l'Académie Royale des Sciences, des Lettres et des Beaux-Arts de Belgique. (659) Si l'on tient compte de ces éijualions, les autres Bedingun- gen d'intégrabilité des équations (4) deviennent (a' = -(6).. Les Premiers membres des équations (5), multipliés par e^, respectivement deviennent égaux Aux Trois dérivées Sekunden d-e-d-e-d'e-"dy dz dz dx dx dy Ces équations s'intègrent donc, et donnent, en représen-tant par F, F, F,, des Bewegun arbitraires d-e-" = F (a), Dx d^, - e-=F, {y) dy^e-^'=F, (=); az d'où, par une nouvelle intégration e& Stockfoto$

RMRGTB5H–. Bulletin de l'Académie Royale des Sciences, des Lettres et des Beaux-Arts de Belgique. (659) Si l'on tient compte de ces éijualions, les autres Bedingun- gen d'intégrabilité des équations (4) deviennent (a' = -(6).. Les Premiers membres des équations (5), multipliés par e^, respectivement deviennent égaux Aux Trois dérivées Sekunden d-e-d-e-d'e-"dy dz dz dx dx dy Ces équations s'intègrent donc, et donnent, en représen-tant par F, F, F,, des Bewegun arbitraires d-e-" = F (a), Dx d^, - e-=F, {y) dy^e-^'=F, (=); az d'où, par une nouvelle intégration e&

. Abhandlungen der Königlich Bayerischen Akademie, Christian, mathematisch-physikalische Klasse. Wissenschaft. 17 3 lo-m dX3 Lg m d^m3 &Lt;P d^dx dlgm d dl/" ist aber nach (9) bereits als Funktion von Ö> berechnet (bis auf Glieder e^); gs-ist-ß) dlgmdW auch nur noch^ als Funktion von x und y auszudrücken. Vor Ausführung of this Aufgabe überlegen wir, daß y-mit-Differentialquotienten (im Allgemeinen) nur klein sein wird, dass wir auch für eine erste Näherung höhere Potenzen?, dy 1, •,,. ,.T,/^N •, Dgm,,., Slgm, 3 lgw. T y und -^- vernachlässigen dürfen. JNach (9) i Stockfoto

RMRR82YR–. Abhandlungen der Königlich Bayerischen Akademie, Christian, mathematisch-physikalische Klasse. Wissenschaft. 17 3 lo-m dX3 Lg m d^m3 &Lt;P d^dx dlgm d dl/" ist aber nach (9) bereits als Funktion von Ö> berechnet (bis auf Glieder e^); gs-ist-ß) dlgmdW auch nur noch^ als Funktion von x und y auszudrücken. Vor Ausführung of this Aufgabe überlegen wir, daß y-mit-Differentialquotienten (im Allgemeinen) nur klein sein wird, dass wir auch für eine erste Näherung höhere Potenzen?, dy 1, •,,. ,.T,/^N •, Dgm,,., Slgm, 3 lgw. T y und -^- vernachlässigen dürfen. JNach (9) i

. Acta Societatis Scientiarum Fennicae. Wissenschaft. Hj. Tallqvist. Hier sind a und b beliebige Constante; sterben Funktion F enthält eine unbestimmte additive Constante, sterben aber keinen Einfluss auf die Arbeit W hat. Würde der Mensch verlangen, dass für x=x, y=Yo, F gleich Null sei, so hätte man einfach X {x, ij) dx + Y{xo, y) dy, W = F{x, y). Funktion F sterben, welche ja auch sterben Kräftefunction genannt wird, ist in dem jetzt betrachteten Falle in der ganzen Ebene eindeutig, abgesehen natürlich von der Constanten C, der Mann sich einen bestimmten Wert beigelegt zu denken hat. Denn die Funktion F kann, wie d Stockfoto

RMRR3RDY–. Acta Societatis Scientiarum Fennicae. Wissenschaft. Hj. Tallqvist. Hier sind a und b beliebige Constante; sterben Funktion F enthält eine unbestimmte additive Constante, sterben aber keinen Einfluss auf die Arbeit W hat. Würde der Mensch verlangen, dass für x=x, y=Yo, F gleich Null sei, so hätte man einfach X {x, ij) dx + Y{xo, y) dy, W = F{x, y). Funktion F sterben, welche ja auch sterben Kräftefunction genannt wird, ist in dem jetzt betrachteten Falle in der ganzen Ebene eindeutig, abgesehen natürlich von der Constanten C, der Mann sich einen bestimmten Wert beigelegt zu denken hat. Denn die Funktion F kann, wie d

$. Bulletin international de l'Acadmie des sciences de Cracovie, Classe des Sciences mathmatiques et Naturelles. Wissenschaft; Naturgeschichte; Natural History - - Polen. - K'r).' - 'i^r) (24) tp{x, y, z) = // ^ All+^^^ l2 + 9 x' 9 y' 9 y' dx j^^^^^^^ Cr) "dy" dz "cJz" dz "Lorsque le point {x^y.z) est ext^ rieur au domaine {D a: (25) t^(x, y, z) = f{x, y, z) puisque dans ce cas, ich 'int^ grale (4) est nuUe par Hypothese. II SUT-fira getan de raisonner comme au § 7 Gießen reconnaitre que la fonc- ip (Ar, y, z) neigen, einheitliche^ ment Vers une Funktion fortsetzen, d6-finie sur la Frontiere (S) du domaine{I) Stockfoto$

RMRGNGDM–. Bulletin international de l'Acadmie des sciences de Cracovie, Classe des Sciences mathmatiques et Naturelles. Wissenschaft; Naturgeschichte; Natural History - - Polen. - K'r).' - 'i^r) (24) tp{x, y, z) = // ^ All+^^^ l2 + 9 x' 9 y' 9 y' dx j^^^^^^^ Cr) "dy" dz "cJz" dz "Lorsque le point {x^y.z) est ext^ rieur au domaine {D a: (25) t^(x, y, z) = f{x, y, z) puisque dans ce cas, ich 'int^ grale (4) est nuUe par Hypothese. II SUT-fira getan de raisonner comme au § 7 Gießen reconnaitre que la fonc- ip (Ar, y, z) neigen, einheitliche^ ment Vers une Funktion fortsetzen, d6-finie sur la Frontiere (S) du domaine{I)

. Comptesrendusheb 74 acad.Es NATURELLES. (I-'Ã®") au Plan oscillateur de l'une des Linien de courbure,. dl dl dl3y-cos^fx Sünde | L'". - L - 3 - j - cosp. sin-FJ. 4 - sünde' s. /; Dans cette Ã©quation,-et-Dekor courbures signent Les principales de la Oberfläche, d^dl rfi dl â â â â De constantes proportionnelles aux Variationen que ces dx dy d.r Dj '''courbures subissent, lorsqu'on passe de l'origine À un-Nummer infiniment Voisin sur l'une ou l'autre des Linien de courbure. Â"en reprÃ©sentant par le coelficient de X° dans la formule prÃ© Cà © Dente, et Par-la courbure qui entsprechen à l' Stockfoto

RMRED0CG–. Comptesrendusheb 74 acad.Es NATURELLES. (I-'Ã®") au Plan oscillateur de l'une des Linien de courbure,. dl dl dl3y-cos^fx Sünde | L'". - L - 3 - j - cosp. sin-FJ. 4 - sünde' s. /; Dans cette Ã©quation,-et-Dekor courbures signent Les principales de la Oberfläche, d^dl rfi dl â â â â De constantes proportionnelles aux Variationen que ces dx dy d.r Dj '''courbures subissent, lorsqu'on passe de l'origine À un-Nummer infiniment Voisin sur l'une ou l'autre des Linien de courbure. Â"en reprÃ©sentant par le coelficient de X° dans la formule prÃ© Cà © Dente, et Par-la courbure qui entsprechen à l'

. Atti della Accademia Nazionale dei Lincei". le derivazioni membro del Secondo ora prima del cangiamento intendendosi fatte di Variabile: e evidentemente perciÃ² sarÃ: IdR l dR 00 de 1^' d à € dR dUdR dB, di dX d d Dr.^^^ â di, ovvero:. F (H) d di Ã¬ Vj) 1 ICH di^^ würde/ IR d^d^'Ove: 2 y ().) = ( - ) "1 dR! - X d'Y, si schließen che Pei punti e poichÃ© Ergebnisse analoguehi si Hanno Pro,, d-Fi' d^' esterni all'Bereich ellittica anche le Derivate seconde di V sono finite e Weiter e si ha: Ein "V F (H). Bitte beachten Sie, dass diese Bilder aus gescannten Seite Bilder, die digital wurden extrahiert werden Stockfoto

RMRT0HR9–. Atti della Accademia Nazionale dei Lincei". le derivazioni membro del Secondo ora prima del cangiamento intendendosi fatte di Variabile: e evidentemente perciÃ² sarÃ: IdR l dR 00 de 1^' d à € dR dUdR dB, di dX d d Dr.^^^ â di, ovvero:. F (H) d di Ã¬ Vj) 1 ICH di^^ würde/ IR d^d^'Ove: 2 y ().) = ( - ) "1 dR! - X d'Y, si schließen che Pei punti e poichÃ© Ergebnisse analoguehi si Hanno Pro,, d-Fi' d^' esterni all'Bereich ellittica anche le Derivate seconde di V sono finite e Weiter e si ha: Ein "V F (H). Bitte beachten Sie, dass diese Bilder aus gescannten Seite Bilder, die digital wurden extrahiert werden

. Atti della R. Accademia delle Regional di Torino. Wissenschaft; Natural History. 154 VITO VOLTERRA Comunque siano disposti i punti Ai, 7>,, Cj, Dy, A, B, C^^!)^, avremo in alcune porzioni del contorno (A.y B^e C^J)^nella Abb. IH), Abb. Ili C in altre (A^C^e BiDi). Ein 'e nelle rimanenti ^w^ © 3. © 3-7 - &Lt;0 Eine kommen facilmente Si può verificare. Ne segue che Ds<0 in Cui l'integrale è esteso Al contorno 5 del cerchio H. Ora è Questa formola evidentemente assurda, perchè è Noto che J^dn Jj dx j dy dH, in Cui il secondo integrale è esteso Ein tutto il cerchio H. Le condizioni imposte Stockfoto

RMRJTKN6–. Atti della R. Accademia delle Regional di Torino. Wissenschaft; Natural History. 154 VITO VOLTERRA Comunque siano disposti i punti Ai, 7>,, Cj, Dy, A, B, C^^!)^, avremo in alcune porzioni del contorno (A.y B^e C^J)^nella Abb. IH), Abb. Ili C in altre (A^C^e BiDi). Ein 'e nelle rimanenti ^w^ © 3. © 3-7 - &Lt;0 Eine kommen facilmente Si può verificare. Ne segue che Ds<0 in Cui l'integrale è esteso Al contorno 5 del cerchio H. Ora è Questa formola evidentemente assurda, perchè è Noto che J^dn Jj dx j dy dH, in Cui il secondo integrale è esteso Ein tutto il cerchio H. Le condizioni imposte

. Acta Societatis Scientiarum Fennicae. Wissenschaft. (15) Hj.t alle q Vist. dx d-y dy d-x Es Tlr^ dt dt-I/f'^-V m'Hm worin Roi sterben mit ihrem Zeichen gerechnete Geschwindiglveit des Punktes S ist und der Krümmungsradius g Positif" in der Richtung von S / C gerechnet wird. Er ist gleich auch B,, in dem Verhältnis vermindert. l; l+^), somit speziell für Punkte der Tangente in C gleich B und für Punkte der Normalen in C gleich R B^a, (16) (1) + Ra) + u Reo In den Ausdruck (15) kann man sterben Krümmungsradien der Polkurven im Punkte C einführen. Es sei da = ds positiv. Man berechnet aus (6a) durch Dif Stockfoto

RMRR3KYD–. Acta Societatis Scientiarum Fennicae. Wissenschaft. (15) Hj.t alle q Vist. dx d-y dy d-x Es Tlr^ dt dt-I/f'^-V m'Hm worin Roi sterben mit ihrem Zeichen gerechnete Geschwindiglveit des Punktes S ist und der Krümmungsradius g Positif" in der Richtung von S / C gerechnet wird. Er ist gleich auch B,, in dem Verhältnis vermindert. l; l+^), somit speziell für Punkte der Tangente in C gleich B und für Punkte der Normalen in C gleich R B^a, (16) (1) + Ra) + u Reo In den Ausdruck (15) kann man sterben Krümmungsradien der Polkurven im Punkte C einführen. Es sei da = ds positiv. Man berechnet aus (6a) durch Dif

$. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. 52 MATHÃMATIQUES, Astronomie, GÃODÃSIE ET MÃCANIQUE il vient pour l'abscisse#, x = R (a-p-Sünde a), sans avoir de constante à Ajouter à Si t choisit convenablement l'origine sur la droite OX. La Courbe est donc la cycloÃ ¯ de engendrÃ©e par le Rou-Lement sur l'Ax OX du Cercle De rayon R.2 Â° Faisons g{^{y) f=2 Ky, le Koeffizient K reprÃ©sentant un Nombre konstant. Il viendra dx = dy 4> dy& y - y/k â Ich Ã©quation diffÃ©rentielle d'une droite dont le Coefficient d'inclinaison Est/K â 1. Si l'on Donne À K la valeurâ Â" plus Grande que l'un Stockfoto$

RMREDA2R–. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. 52 MATHÃMATIQUES, Astronomie, GÃODÃSIE ET MÃCANIQUE il vient pour l'abscisse#, x = R (a-p-Sünde a), sans avoir de constante à Ajouter à Si t choisit convenablement l'origine sur la droite OX. La Courbe est donc la cycloÃ ¯ de engendrÃ©e par le Rou-Lement sur l'Ax OX du Cercle De rayon R.2 Â° Faisons g{^{y) f=2 Ky, le Koeffizient K reprÃ©sentant un Nombre konstant. Il viendra dx = dy 4> dy& y - y/k â Ich Ã©quation diffÃ©rentielle d'une droite dont le Coefficient d'inclinaison Est/K â 1. Si l'on Donne À K la valeurâ Â" plus Grande que l'un

. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. 6 MATHÃMATIQUES, Astronomie, GÃODÃSIE ET MÃCANIQUE auf Dekor duit, en prenant la Dekor rivÃ©e logarithmique des Deux membres^ dr dy d(cos Â") F (Â") doi,^-T^,. + Tang ein Â" ein. r(a) '^r y cos ein. Multiplions de Part et d'autre par Kinderbett Â", il vient F (a) dh-F (Â") Kinderbett eine dx-r/a, et en indiquant La Quadrature Ã exÃ©Niedlicher, (i 3) e = 0 o+" "+r^cotÂ" rfÂ", Ã©quation qui, Jointe à l'Ã©quation (i4) F (Â") cos a'Rei) rÃ©sente La Courbe GH en coordonnÃ©es Alles aus Fleece. Les signes que Nous avons adoptÃ © s sind ceux qui Correspondent à l'Ã©tat de la Abbildung; dans Ch Stockfoto

RMREDBTN–. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. 6 MATHÃMATIQUES, Astronomie, GÃODÃSIE ET MÃCANIQUE auf Dekor duit, en prenant la Dekor rivÃ©e logarithmique des Deux membres^ dr dy d(cos Â") F (Â") doi,^-T^,. + Tang ein Â" ein. r(a) '^r y cos ein. Multiplions de Part et d'autre par Kinderbett Â", il vient F (a) dh-F (Â") Kinderbett eine dx-r/a, et en indiquant La Quadrature Ã exÃ©Niedlicher, (i 3) e = 0 o+" "+r^cotÂ" rfÂ", Ã©quation qui, Jointe à l'Ã©quation (i4) F (Â") cos a'Rei) rÃ©sente La Courbe GH en coordonnÃ©es Alles aus Fleece. Les signes que Nous avons adoptÃ © s sind ceux qui Correspondent à l'Ã©tat de la Abbildung; dans Ch

$. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. s. GUIEYSSE. ÉTUDE SUR LES SONDAGES 223 124) ou{h-X) = E dx"^' 1 + dx-dt En négligeant en première Angleichung-y-r, auf obtient y = P E 1 2 d'où la Flèche observée Gießen: P ¥ X El 2 II E I3 (24') 3 GX' pour l'Équation de La Courbe; d'où dy=- ^-^[/i--{h-xf] c/a;;;;;;;; la valeur de La Castre en B est-j -='", Quantité fort Petite en Général, puisque l'on peut toujours prendre h assez Grand, et que le Courant ne dépassant jamais Deux noeuds (1 Noeud herum = 4,852 Mètres), la Vitesse^ est au plus de 1 Meter Par seconde, beaucoup plus Stockfoto$

RMREDNKD–. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. s. GUIEYSSE. ÉTUDE SUR LES SONDAGES 223 124) ou{h-X) = E dx"^' 1 + dx-dt En négligeant en première Angleichung-y-r, auf obtient y = P E 1 2 d'où la Flèche observée Gießen: P ¥ X El 2 II E I3 (24') 3 GX' pour l'Équation de La Courbe; d'où dy=- ^-^[/i--{h-xf] c/a;;;;;;;; la valeur de La Castre en B est-j -='", Quantité fort Petite en Général, puisque l'on peut toujours prendre h assez Grand, et que le Courant ne dépassant jamais Deux noeuds (1 Noeud herum = 4,852 Mètres), la Vitesse^ est au plus de 1 Meter Par seconde, beaucoup plus

. Acta Societatis Scientiarum Fennicae. Wissenschaft. 480 Hj. Tallqvist. Abb. 2.. J r Bezeichnet man wieder sterben Coordinaten des Punktes P der Kurve (siehe Abb. 2) mit x, y und z, so erhält man für die Bestimmung der Richtungscosinus X, Y und Z der Normale der Minimalfläche in diesem Punkte sterben Gl. X2 - f Y 2 + Z" = 1, Xdx + Ydy-j-Zdz - 0, 2. V YJ - Z = Cos, r r r durch deren Auflösung (vergleiche Sterben das System 3) Ausdrücke sin Co,,, x-a. (S-c) dy- 0/- b) ds. X=cos Co + - - - = -^r-ras-Y=y -. (X-a) Gd - (z-c) dx. cos Co+-sin Co, r-rds r, z-c, (es-b) dx - (x Stockfoto

RMRR3744–. Acta Societatis Scientiarum Fennicae. Wissenschaft. 480 Hj. Tallqvist. Abb. 2.. J r Bezeichnet man wieder sterben Coordinaten des Punktes P der Kurve (siehe Abb. 2) mit x, y und z, so erhält man für die Bestimmung der Richtungscosinus X, Y und Z der Normale der Minimalfläche in diesem Punkte sterben Gl. X2 - f Y 2 + Z" = 1, Xdx + Ydy-j-Zdz - 0, 2. V YJ - Z = Cos, r r r durch deren Auflösung (vergleiche Sterben das System 3) Ausdrücke sin Co,,, x-a. (S-c) dy- 0/- b) ds. X=cos Co + - - - = -^r-ras-Y=y -. (X-a) Gd - (z-c) dx. cos Co+-sin Co, r-rds r, z-c, (es-b) dx - (x

. Acta Societatis Scientiarum Fennicae. Wissenschaft. Systèmes rundet et Invarianten différentiels. 55:00 - a, d'après Le n9, C RF? Ich w/C (/? DTi., d (^.^ dx dx^^" dz "d d d^ dy ôy^^ dz) ôpi et de àjj déduisant ôqi se et dq en y remplaçant 2^ et q par jh et f/, (voir Le n° 7). L'équation (S) devient alors, en Tenant compte de la relation (7), +- 0, et comme cette équation doit avoir lieu poiu - toutes les valeurs de p, q, P, Q, qui satisfont à la relation (7), il straff qu'auf Ait séparément (9) Ä:. + d-I = "dy^^""^ dz dz-dx = '^J-0^=°' 5^+^l/=" - Il s'ag Stockfoto

RMRR36NJ–. Acta Societatis Scientiarum Fennicae. Wissenschaft. Systèmes rundet et Invarianten différentiels. 55:00 - a, d'après Le n9, C RF? Ich w/C (/? DTi., d (^.^ dx dx^^" dz "d d d^ dy ôy^^ dz) ôpi et de àjj déduisant ôqi se et dq en y remplaçant 2^ et q par jh et f/, (voir Le n° 7). L'équation (S) devient alors, en Tenant compte de la relation (7), +- 0, et comme cette équation doit avoir lieu poiu - toutes les valeurs de p, q, P, Q, qui satisfont à la relation (7), il straff qu'auf Ait séparément (9) Ä:. + d-I = "dy^^""^ dz dz-dx = '^J-0^=°' 5^+^l/=" - Il s'ag

$. Acta Societatis Scientiarum Fennicae. Wissenschaft. In der mathematischen Ueher Årheitsgrössen Physilc 4. Um das Ringen um 0 genommene Integral der Arbeit näher zu untersuchen, wählen wir 0 als Anfangspunkt in einem System von Polarcoordinaten. Dabei ergiebt sich (15) (16) (17) (18) x = r cos< f, y=r sintp.. r=}/x^+//2; tg< p =^. Ich dx= cos Wenn dr-r sin &Lt;y-d (p, (Dy=sin tp-dr--r cos(f d (p. Abb. 5. rdr = Xdx - ydy, R^d<p=xdy - ydx. Das linienintegral verwandelt sich in (19) I{Xdx + Ydy)=I {{X cos y + I in ip) dr + (-X sin y + y cos y) r FDR-|, ein:; und y m X und F Stockfoto$

RMRR3RDG–. Acta Societatis Scientiarum Fennicae. Wissenschaft. In der mathematischen Ueher Årheitsgrössen Physilc 4. Um das Ringen um 0 genommene Integral der Arbeit näher zu untersuchen, wählen wir 0 als Anfangspunkt in einem System von Polarcoordinaten. Dabei ergiebt sich (15) (16) (17) (18) x = r cos< f, y=r sintp.. r=}/x^+//2; tg< p =^. Ich dx= cos Wenn dr-r sin &Lt;y-d (p, (Dy=sin tp-dr--r cos(f d (p. Abb. 5. rdr = Xdx - ydy, R^d<p=xdy - ydx. Das linienintegral verwandelt sich in (19) I{Xdx + Ydy)=I {{X cos y + I in ip) dr + (-X sin y + y cos y) r FDR-|, ein:; und y m X und F

. Atti della Accademia Nazionale dei Lincei". Â 314â Moltiplicando questa equazione Pel prodotto dy dz, avremo. dV-[I" "'dUdV, d>) dz - Dy dz â â dx, dx dx Co.^ dx 1^00 'DU dV^â â DX, DX DX X, equazione, che potrÃ scriversi anche nel Modo seguente: X, CD, x â â dx dy Dz. dx dx x^Il primo membro di Questa equazione rappresenta La Massa di un Corpo, avente V pro densitÃ Variabile U â^, mentre v chiamando il Volume del Corpo stesso, abbiamo CliV dv = dx dy Dz. Del resto dy dz rappresenta un elemento della superficie totale del Corpo, proiettato sul Piano YZ; perciÃ² chi Stockfoto

RMRJW5KF–. Atti della Accademia Nazionale dei Lincei". Â 314â Moltiplicando questa equazione Pel prodotto dy dz, avremo. dV-[I" "'dUdV, d>) dz - Dy dz â â dx, dx dx Co.^ dx 1^00 'DU dV^â â DX, DX DX X, equazione, che potrÃ scriversi anche nel Modo seguente: X, CD, x â â dx dy Dz. dx dx x^Il primo membro di Questa equazione rappresenta La Massa di un Corpo, avente V pro densitÃ Variabile U â^, mentre v chiamando il Volume del Corpo stesso, abbiamo CliV dv = dx dy Dz. Del resto dy dz rappresenta un elemento della superficie totale del Corpo, proiettato sul Piano YZ; perciÃ² chi

. Comptesrendusheb 1311900 acad.Es NATURELLES. (488) "Les constantes Gemeinden k z^z.,,. .., Zâ se sentent prÃ© aussi dans la Funktion c; il faudra, Gießen ndus trouver dans le cas que nous considÃ©Rons, que l'intÃ©grale Générale du systÃ¨me (3) Dekor pende d'au * une constante arbitraire. Oder, l'intÃ©grale Générale de (3) ne peut Dekor pendre, en Dehors de la constante Additiv, au plus que d'une constante arbitraire, et pour que ce fait Ait lieu, il faut et il suffÃ® t que c soit Dekor finie Par1^c dsc I db^b dx ib. Ich Oc c dy ich da ein dy La, ce qui prouve que la Funktion c peut Ãªtre trouvÃ Stockfoto

RMREBG75–. Comptesrendusheb 1311900 acad.Es NATURELLES. (488) "Les constantes Gemeinden k z^z.,,. .., Zâ se sentent prÃ© aussi dans la Funktion c; il faudra, Gießen ndus trouver dans le cas que nous considÃ©Rons, que l'intÃ©grale Générale du systÃ¨me (3) Dekor pende d'au * une constante arbitraire. Oder, l'intÃ©grale Générale de (3) ne peut Dekor pendre, en Dehors de la constante Additiv, au plus que d'une constante arbitraire, et pour que ce fait Ait lieu, il faut et il suffÃ® t que c soit Dekor finie Par1^c dsc I db^b dx ib. Ich Oc c dy ich da ein dy La, ce qui prouve que la Funktion c peut Ãªtre trouvÃ

. Comptes Rendus hebdomadaires des sÃ© ances de l'AcadÃ©mie des Sciences. Wissenschaft - Gesellschaften, etc.; Wissenschaft; Wissenschaft. une Sorte de Cylindre, dont les bases sind sur S et E, et dont la Oberfläche latÃ©-rale est constituÃ©e par la Suite des normales PP,. Appliquons la Formule (2) à la Oberfläche limitant ce-Band. Sur les deux Grundlagen is est Nul: Il ne subsiste donc, dans l'intÃ©grale (2), que la Partie relative à la Oberfläche latÃ©rale. Pour l'Ã©crire appelons, a, p,-y Les cosinus directeurs de la normale PN EN P À la Oberfläche latÃ©rale, dx, dy, dz les Projektionen d'un Ã©lÃ©ment PP' = f/i de la ligne C, Stockfoto

RMRECEP2–. Comptes Rendus hebdomadaires des sÃ© ances de l'AcadÃ©mie des Sciences. Wissenschaft - Gesellschaften, etc.; Wissenschaft; Wissenschaft. une Sorte de Cylindre, dont les bases sind sur S et E, et dont la Oberfläche latÃ©-rale est constituÃ©e par la Suite des normales PP,. Appliquons la Formule (2) à la Oberfläche limitant ce-Band. Sur les deux Grundlagen is est Nul: Il ne subsiste donc, dans l'intÃ©grale (2), que la Partie relative à la Oberfläche latÃ©rale. Pour l'Ã©crire appelons, a, p,-y Les cosinus directeurs de la normale PN EN P À la Oberfläche latÃ©rale, dx, dy, dz les Projektionen d'un Ã©lÃ©ment PP' = f/i de la ligne C,

$. Bulletin de la SociÃ©tÃ© impÃ©riale des naturalistes de Moscou. Wissenschaft; Biologie; Geologie; Natural History. 375 Ñ{^, Ð', Ñ, CJ = Ð¾, de laquelle il rÃ©sulte Que, dans la couche supperficielle, J est une Funktion de n seulenaent, de maniÃ¨re qu'une Oberfläche quelconque parallÃ¨le À la Oberfläche libre Aura dans tous ces Punkte la mÃªme densitÃ ©. Auswirkungen Analoga des consÃ©rÃ©sultent des Bedingungen de l'Ã©quilibre des Punkte prÃ¨s De parois du Vase. Ces- bedingungen Ã©tant dx ð¤) D!A-Ð°{Ñ dx' df/dX-Ð¹ Ð¤) 'Ð¹Ð ±, -+ Ñ) i = J^ ^-^ dy dz dz^g. Auf einem dX = Jd (^j-f-Ñ) â gJdz. Soit ABC la Oberfläche in Stockfoto$

RMRGPJJY–. Bulletin de la SociÃ©tÃ© impÃ©riale des naturalistes de Moscou. Wissenschaft; Biologie; Geologie; Natural History. 375 Ñ{^, Ð', Ñ, CJ = Ð¾, de laquelle il rÃ©sulte Que, dans la couche supperficielle, J est une Funktion de n seulenaent, de maniÃ¨re qu'une Oberfläche quelconque parallÃ¨le À la Oberfläche libre Aura dans tous ces Punkte la mÃªme densitÃ ©. Auswirkungen Analoga des consÃ©rÃ©sultent des Bedingungen de l'Ã©quilibre des Punkte prÃ¨s De parois du Vase. Ces- bedingungen Ã©tant dx ð¤) D!A-Ð°{Ñ dx' df/dX-Ð¹ Ð¤) 'Ð¹Ð ±, -+ Ñ) i = J^ ^-^ dy dz dz^g. Auf einem dX = Jd (^j-f-Ñ) â gJdz. Soit ABC la Oberfläche in

$. Bulletin de la Classe physikalisch-mathÂ © - matique de l'AcadÂ © - mie impÂ © - riale des sciences de Saint-P © - tersbourg. Igh J 195 tun lMcadÃ © mÃ¯eSaiMit-de PÃ©tersbourÂ" -. 196 3 Â"*â Â "ffp &Lt;i3 r P = J/J ' x ' dx dy dz=ÃJ^ Jörg j Ã'' = et l'Ã©quation de l'ellipsoÃ ¯ de auxiliaire sera 2' ein; 2 3/2 Cette Oberfläche est circonseriptible au cylindre Gießen e 2 = - Dans le cas particulier de Ox' perpendiculaire au Plan y Oz, cette droite Sera l'un des Achsen de l'ellipsoÃ ¯ de, et par consÃ©Quent, Elle sera aussi un-ax principal du cylindre. Les deux autres Achsen Achsen seront Les principaux de l'Ellipse circonscrite Stockfoto$

RMRGT07X–. Bulletin de la Classe physikalisch-mathÂ © - matique de l'AcadÂ © - mie impÂ © - riale des sciences de Saint-P © - tersbourg. Igh J 195 tun lMcadÃ © mÃ¯eSaiMit-de PÃ©tersbourÂ" -. 196 3 Â"*â Â "ffp &Lt;i3 r P = J/J ' x ' dx dy dz=ÃJ^ Jörg j Ã'' = et l'Ã©quation de l'ellipsoÃ ¯ de auxiliaire sera 2' ein; 2 3/2 Cette Oberfläche est circonseriptible au cylindre Gießen e 2 = - Dans le cas particulier de Ox' perpendiculaire au Plan y Oz, cette droite Sera l'un des Achsen de l'ellipsoÃ ¯ de, et par consÃ©Quent, Elle sera aussi un-ax principal du cylindre. Les deux autres Achsen Achsen seront Les principaux de l'Ellipse circonscrite

. Bulletin de la SociÃ©tÃ© impÃ©riale des naturalistes de Moscou. Wissenschaft; Biologie; Geologie; Natural History. 371 Examinons d'abord les Ã © quations (12). Puisque à un point à une Entfernung sinnvolle de la Surface du Fluide-Teich une valeur constante de^, et Ñ pour ces Punkte se rÃ©duit Ã Zöllner © ro, de mÃªme que Ñ^ les Bedingungen d'Ã©quilibre de ces Punkte seront (/Ð dX dX dx dy dz ou Bien ou enfin d Jgdz = 0; (14) X Ð § - Jgz = C,. . OÃ¹ Ð¡Dekor signe une quantitÃ© constante. Les Bedingungen de l'Ã©quilibre des Punkte prÃ¨s de la sur-face Libre du liquide se Dekor duisent des Ã © quations (12) en y Stockfoto

RMRGPJKB–. Bulletin de la SociÃ©tÃ© impÃ©riale des naturalistes de Moscou. Wissenschaft; Biologie; Geologie; Natural History. 371 Examinons d'abord les Ã © quations (12). Puisque à un point à une Entfernung sinnvolle de la Surface du Fluide-Teich une valeur constante de^, et Ñ pour ces Punkte se rÃ©duit Ã Zöllner © ro, de mÃªme que Ñ^ les Bedingungen d'Ã©quilibre de ces Punkte seront (/Ð dX dX dx dy dz ou Bien ou enfin d Jgdz = 0; (14) X Ð § - Jgz = C,. . OÃ¹ Ð¡Dekor signe une quantitÃ© constante. Les Bedingungen de l'Ã©quilibre des Punkte prÃ¨s de la sur-face Libre du liquide se Dekor duisent des Ã © quations (12) en y

. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. ou Encore:= Fläche ABCD == Fläche ABKE. Auto les deux parallÃ © lograms considÃ©rÃ©s ont mÃªme base AB et mÃªme hauteur, puisque AB et CD sind parallÃ¨les [isothermes Voisines]. Oder, Oberfläche ABKE= dd X dx. Â" 8 Aiiisi oe Idx do=4-dOdx db l 8 dy rfe'AUTRE ZYKLUS (Â") CE-Zyklus ne diffÃ¨re du cycle prÃ© Cà © dent qu'en ce que le systÃ¨me Ã © ändern (Cà ¨ de) entre B et C une quantitÃ© de chaleur Qt, avec des Sources dont les tempÃ© ratures SIND Ã © chelonnÃ © es de 6 à 8 + c? 8, et entre D et A une absorbe quantitÃ© de Chaleur qv avec des Sources don Stockfoto

RMREDAX5–. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. ou Encore:= Fläche ABCD == Fläche ABKE. Auto les deux parallÃ © lograms considÃ©rÃ©s ont mÃªme base AB et mÃªme hauteur, puisque AB et CD sind parallÃ¨les [isothermes Voisines]. Oder, Oberfläche ABKE= dd X dx. Â" 8 Aiiisi oe Idx do=4-dOdx db l 8 dy rfe'AUTRE ZYKLUS (Â") CE-Zyklus ne diffÃ¨re du cycle prÃ© Cà © dent qu'en ce que le systÃ¨me Ã © ändern (Cà ¨ de) entre B et C une quantitÃ© de chaleur Qt, avec des Sources dont les tempÃ© ratures SIND Ã © chelonnÃ © es de 6 à 8 + c? 8, et entre D et A une absorbe quantitÃ© de Chaleur qv avec des Sources don

. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. KD. COLLIGNON. Â PROBLÃME DE MÃCAMQU 1 M systÃ¨me De tangentes À la courbe Um donc une Horloge ou un mÃ©tronome. Les rayone vecteurs &Lt;le La Courbe auxiliaire/(. S'normale supérieure À MN. Si cette durÃ©e est reprÃ©sentÃ©e par â l (y), auf devra avoir l'Ã©quation. }/2 MS "9 ou Bien m. Wj-^ Ici les Variablen x et y avec s figurent dans l'Ã©quation diffÃ©rentielle. § RemplaÃ ons ds * Gleichheit dx " 1-f-dy 2] il viendra en rÃ©solvant par rapport À-DX, DX - dy J"';". V (jMijf - - lu La Lösung s'obtient par Quadrature. Il Faut pour que l'abscisse x s Stockfoto

RMREDA31–. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. KD. COLLIGNON. Â PROBLÃME DE MÃCAMQU 1 M systÃ¨me De tangentes À la courbe Um donc une Horloge ou un mÃ©tronome. Les rayone vecteurs &Lt;le La Courbe auxiliaire/(. S'normale supérieure À MN. Si cette durÃ©e est reprÃ©sentÃ©e par â l (y), auf devra avoir l'Ã©quation. }/2 MS "9 ou Bien m. Wj-^ Ici les Variablen x et y avec s figurent dans l'Ã©quation diffÃ©rentielle. § RemplaÃ ons ds * Gleichheit dx " 1-f-dy 2] il viendra en rÃ©solvant par rapport À-DX, DX - dy J"';". V (jMijf - - lu La Lösung s'obtient par Quadrature. Il Faut pour que l'abscisse x s

. Acta Societatis Scientiarum Fennicae. Wissenschaft. 50 S. D U H E M.. 31) ^ Hzl ÔH dx du dy du dz 4: dx dy dz ds ds ds DM DM DM dx dy dz dx dy' 'dl dl dl u ds'étant une Funktion tinie, weiter et uniforme d'x, y, z, qui peut être en même temps Funktion de x', y', z',, dx ' dy ' dz "DL" dl' dl, et m une Funktion finie, weiter et uniforme d'.//Y'z', qui peut être en même temps Funktion de dx dy dz ds ds ds C'est cette Expression de s q^^'il nous faut maintenant Prüfer. Envisageons Un système formé par un solénoïde magnétique fermé et par un Courant réalisable ouvert, dont l'intensité Stockfoto

RMRR372R–. Acta Societatis Scientiarum Fennicae. Wissenschaft. 50 S. D U H E M.. 31) ^ Hzl ÔH dx du dy du dz 4: dx dy dz ds ds ds DM DM DM dx dy dz dx dy' 'dl dl dl u ds'étant une Funktion tinie, weiter et uniforme d'x, y, z, qui peut être en même temps Funktion de x', y', z',, dx ' dy ' dz "DL" dl' dl, et m une Funktion finie, weiter et uniforme d'.//Y'z', qui peut être en même temps Funktion de dx dy dz ds ds ds C'est cette Expression de s q^^'il nous faut maintenant Prüfer. Envisageons Un système formé par un solénoïde magnétique fermé et par un Courant réalisable ouvert, dont l'intensité

. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. Abb. 3. Fi G. Termes, La projection de M'sur OM se fait en un-Punkt H qui, à la Limite, est le milieu de OM. Ce-thÃ© orÃ¨me n'est Plus exakte, si le point 0 est un point d'finanzaktien. Soient (Abb. 4) x, y Les coordonnÃ©es de M:. r',y' Celles du Punkt M'; tellement Web Content Anzeige sur OM que la castre M'T soit parallÃ¨le Ã OM. Auf einem, en posant, OM OM=s' = s': x= Xs-^X^ + Â"2/â A.S j • • • y ' = B "Ich" - w. . Et, par consÃ©quent: dx ' = (A + 2 AY,.. .) Ds", "DY" = (3B "-f-.. .) S'hls'. Dy'Le Koeffizient angulaire de M'T Ã©tant-r-7> Stockfoto

RMREDN45–. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. Abb. 3. Fi G. Termes, La projection de M'sur OM se fait en un-Punkt H qui, à la Limite, est le milieu de OM. Ce-thÃ© orÃ¨me n'est Plus exakte, si le point 0 est un point d'finanzaktien. Soient (Abb. 4) x, y Les coordonnÃ©es de M:. r',y' Celles du Punkt M'; tellement Web Content Anzeige sur OM que la castre M'T soit parallÃ¨le Ã OM. Auf einem, en posant, OM OM=s' = s': x= Xs-^X^ + Â"2/â A.S j • • • y ' = B "Ich" - w. . Et, par consÃ©quent: dx ' = (A + 2 AY,.. .) Ds", "DY" = (3B "-f-.. .) S'hls'. Dy'Le Koeffizient angulaire de M'T Ã©tant-r-7>

. Bulletin de l'AcadÃ©mie Royale des Sciences, des Lettres et des Beaux-Arts de Belgique. (10) trÃ© que x et y Ã©tant des Bewegun de t et de u, et faisant dx=^ dt H-Srfw; dy=Tdt-^ Udu, la valeur deffZdxdy, Ã©tendue à toutes les valeurs Treffer de j:; et de y, Ã©Tait Ã © gale Ã y^Z (RUâST) dldu, Ã©galement Ã©tendue à toutes les valeurs Treffer de t et de u. Mais mez illustre gÃ©omÃ¨tre n'a pas manquÃ © de faire remarquer que cette Ã©galitÃ© ne s'appliquait qu'aux Valeurs absolues des intÃ©grales. Et rÃ©el-Lement, voici Kommentieren peut se convaincre que le Signe de la Double intÃ©grale j^Z ( Stockfoto

RMRGT35H–. Bulletin de l'AcadÃ©mie Royale des Sciences, des Lettres et des Beaux-Arts de Belgique. (10) trÃ© que x et y Ã©tant des Bewegun de t et de u, et faisant dx=^ dt H-Srfw; dy=Tdt-^ Udu, la valeur deffZdxdy, Ã©tendue à toutes les valeurs Treffer de j:; et de y, Ã©Tait Ã © gale Ã y^Z (RUâST) dldu, Ã©galement Ã©tendue à toutes les valeurs Treffer de t et de u. Mais mez illustre gÃ©omÃ¨tre n'a pas manquÃ © de faire remarquer que cette Ã©galitÃ© ne s'appliquait qu'aux Valeurs absolues des intÃ©grales. Et rÃ©el-Lement, voici Kommentieren peut se convaincre que le Signe de la Double intÃ©grale j^Z (

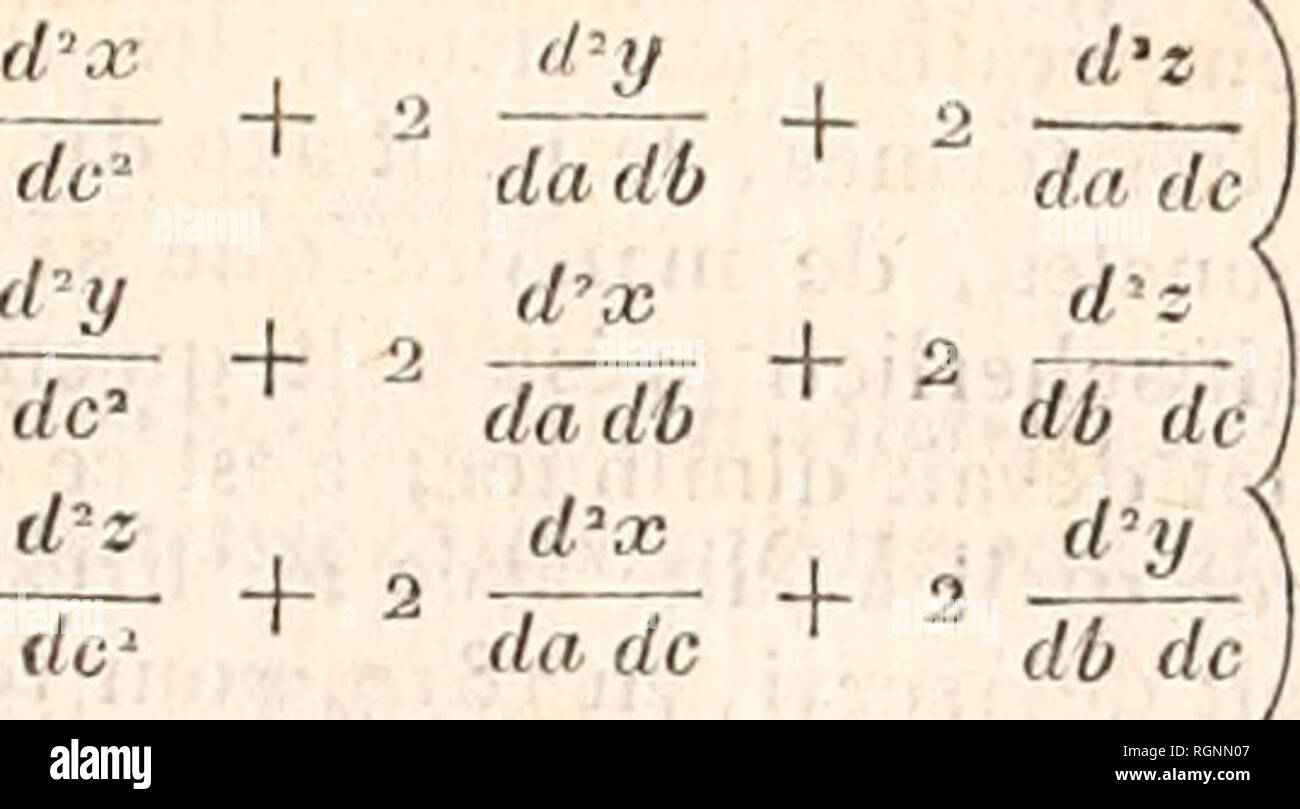. Bulletin des Sciences/par la SociÃ©tÃ© Philomathique de Paris. (Â"Â"*) L'Ã©qualion d'Ã©quilibre ci-dessus donnera donc d'abord les Ã © quations indÃ© finies X =: i Y = fi d'x da' d'y Da'++ Ich d-z d'z d ' z-L e [1 ÃF + cW + Ã' 1 ÃF d'xtW d'y dlF d'z JF '++. qui expriment des Bedingungen Gemeinden à tous les Points du corps. De plus, en nommant/in, n les angles que le plan Tangente à la Oberfläche, Clans le point dont les coordonnÃ©es sind af, h', c', forme avec Les Plans des bc, des Ae et des Au, auf pourra remplacer Dekor "' de' par ds cos l. Da 'tun' par ds cos m, da'd'o'Par ds cos n (MÃ© kann Stockfoto

RMRGNN07–. Bulletin des Sciences/par la SociÃ©tÃ© Philomathique de Paris. (Â"Â"*) L'Ã©qualion d'Ã©quilibre ci-dessus donnera donc d'abord les Ã © quations indÃ© finies X =: i Y = fi d'x da' d'y Da'++ Ich d-z d'z d ' z-L e [1 ÃF + cW + Ã' 1 ÃF d'xtW d'y dlF d'z JF '++. qui expriment des Bedingungen Gemeinden à tous les Points du corps. De plus, en nommant/in, n les angles que le plan Tangente à la Oberfläche, Clans le point dont les coordonnÃ©es sind af, h', c', forme avec Les Plans des bc, des Ae et des Au, auf pourra remplacer Dekor "' de' par ds cos l. Da 'tun' par ds cos m, da'd'o'Par ds cos n (MÃ© kann

$. Comptesrendusheb 75 acad.Es NATURELLES. Ã': > 6) la Zustand devient donc et la torniule 'f'' = '^Ãª/- "-"!!,/y e -'"= ±permet de l'Ã©crire sous sa forme Dekor verbindlichen f&^/M db Ty (La dx •. f'ti, d,1 dx, fd, db d, ^J-TFrY ^.^ j-^H^Jd^-d'J{, dh d, dn 1) Gießen exprimer Ã¢ x et r/r en Funktion de r/z, il faut que les Ã©crire pro-jections de AA' sur BX et DURCH sind diese Formeln nulles; mes donnent immÃ©dia-tement Dx - + c) 4-dy" - ^+ r/r V=o" 2/-^ dy dl Dx -^- h Dr (-- h c]+ DZ-1^=o. D.r 2 / "2 Eliminant dx, dy, dz, auf obtient l'Ã©quation. = o. (Pae Dekor endlichen le systÃ¨m Stockfoto$

RMRED097–. Comptesrendusheb 75 acad.Es NATURELLES. Ã': > 6) la Zustand devient donc et la torniule 'f'' = '^Ãª/- "-"!!,/y e -'"= ±permet de l'Ã©crire sous sa forme Dekor verbindlichen f&^/M db Ty (La dx •. f'ti, d,1 dx, fd, db d, ^J-TFrY ^.^ j-^H^Jd^-d'J{, dh d, dn 1) Gießen exprimer Ã¢ x et r/r en Funktion de r/z, il faut que les Ã©crire pro-jections de AA' sur BX et DURCH sind diese Formeln nulles; mes donnent immÃ©dia-tement Dx - + c) 4-dy" - ^+ r/r V=o" 2/-^ dy dl Dx -^- h Dr (-- h c]+ DZ-1^=o. D.r 2 / "2 Eliminant dx, dy, dz, auf obtient l'Ã©quation. = o. (Pae Dekor endlichen le systÃ¨m

$. Bulletin de la SociÃ©tÃ© impÃ©riale des naturalistes de Moscou. Wissenschaft; Biologie; Geologie; Natural History. 381 À-ds=UTÃ' x) dy H-UTdy) dx p d (SzâpSxâq'^y) q d^xâqSy Szâp '^^r dx dy= J [tSx T^^ zâpSxâq yj] dy ']' Jo dxdy ii Y{^ - P^^"--9^y) Ich dx - pSx - 5%) dxdy Ð³,. Ich dx oÃ¹ les Ausdrücke TÃ'x - + - -{6 zâpÃxâq^ ij,; TÃ'y-^-^ (azâp xâqÃy) iodiquent des quantitÃ©s pries Entre des Limits, La pre-miÃ¨re par rapport À x, et la seconde par rapport À-y.â Pour rÃ©unir Sous un Seul signe intÃ©Gral les deux intÃ©- grales simples de cette Ã©quation, qui sind Verwandte à la Projektion sur le pl Stockfoto$

RMRGPJJF–. Bulletin de la SociÃ©tÃ© impÃ©riale des naturalistes de Moscou. Wissenschaft; Biologie; Geologie; Natural History. 381 À-ds=UTÃ' x) dy H-UTdy) dx p d (SzâpSxâq'^y) q d^xâqSy Szâp '^^r dx dy= J [tSx T^^ zâpSxâq yj] dy ']' Jo dxdy ii Y{^ - P^^"--9^y) Ich dx - pSx - 5%) dxdy Ð³,. Ich dx oÃ¹ les Ausdrücke TÃ'x - + - -{6 zâpÃxâq^ ij,; TÃ'y-^-^ (azâp xâqÃy) iodiquent des quantitÃ©s pries Entre des Limits, La pre-miÃ¨re par rapport À x, et la seconde par rapport À-y.â Pour rÃ©unir Sous un Seul signe intÃ©Gral les deux intÃ©- grales simples de cette Ã©quation, qui sind Verwandte à la Projektion sur le pl

. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. ÃD. COLLIGNON. Â PROBLÃME DE MÃCANIQUE si Tonne veut que./â soit Nulle lorsque y a la valeur a, Bon nain auf Trouve comme rÃ©sultat la Parabole.'/a la rapportÃ©e Ã Sohn ax La Funktion Ã© intÃ grüner devient alors dx = dy Iy-.! J-r-y-2 j/ydy Eine et la courbe clierchÃ©e est la Parabole y* = ax rapportÃ©e Ã Sohn ax liori Gungsschrauben et à la Castre au Sommet. Auf einem, en Effet, en Ã © levant NS' (Abb. 9) perpen-diculaire À la normale MN, jusqu'à la Rencontre de l'ordonnÃ © e MP prolongÃ©e, MS' = MP-fPS'=w-f-, y puisque PN, sous normale, est Ã©Gale à la Cons - Stockfoto

RMREDA2K–. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. ÃD. COLLIGNON. Â PROBLÃME DE MÃCANIQUE si Tonne veut que./â soit Nulle lorsque y a la valeur a, Bon nain auf Trouve comme rÃ©sultat la Parabole.'/a la rapportÃ©e Ã Sohn ax La Funktion Ã© intÃ grüner devient alors dx = dy Iy-.! J-r-y-2 j/ydy Eine et la courbe clierchÃ©e est la Parabole y* = ax rapportÃ©e Ã Sohn ax liori Gungsschrauben et à la Castre au Sommet. Auf einem, en Effet, en Ã © levant NS' (Abb. 9) perpen-diculaire À la normale MN, jusqu'à la Rencontre de l'ordonnÃ © e MP prolongÃ©e, MS' = MP-fPS'=w-f-, y puisque PN, sous normale, est Ã©Gale à la Cons -

$. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. E. FO?" TANE. VU. Â SUR LA DÃFORMATION DES CORPS ISOTROPES 197 et en remplaÃ § ant d. (/(Abl. Rfw^ dk dz "dz d. et â par leurs Ausdrücken (22) und (24): Â"91 X tun)^ dx tun ^^ Ich ddi dk+y ^ + ^-^+: {l + lK) hihJls dij d:. J'Dq^ dq,. dy '' dx dy dz dH dy dii - (X + 3 ii.) (0 Ich dq^^ dqs dq dq^+y dx dq. dx dH dx dM dqs dqs dq dq^^-^^ + 2^) S^. d: dqy (^ + 1-) dwj, Tag ^.,, C?o) 2, dk dx dy dz"^^' Dy - (X + 3 Fx) t 02' dx ^ dz "Dq^ dqi dx dE dx f/H f/^^^ 3DQ dq dq^2 (X + 2)^C dv dq. dy dK dy rfH dq^^^ dq dq dq ^ Ainsi auf der Aura à la Surface du corps Ã © l Stockfoto$

RMREDATN–. Compte Rendu. Wissenschaft; Wissenschaft - Kongresse. E. FO?" TANE. VU. Â SUR LA DÃFORMATION DES CORPS ISOTROPES 197 et en remplaÃ § ant d. (/(Abl. Rfw^ dk dz "dz d. et â par leurs Ausdrücken (22) und (24): Â"91 X tun)^ dx tun ^^ Ich ddi dk+y ^ + ^-^+: {l + lK) hihJls dij d:. J'Dq^ dq,. dy '' dx dy dz dH dy dii - (X + 3 ii.) (0 Ich dq^^ dqs dq dq^+y dx dq. dx dH dx dM dqs dqs dq dq^^-^^ + 2^) S^. d: dqy (^ + 1-) dwj, Tag ^.,, C?o) 2, dk dx dy dz"^^' Dy - (X + 3 Fx) t 02' dx ^ dz "Dq^ dqi dx dE dx f/H f/^^^ 3DQ dq dq^2 (X + 2)^C dv dq. dy dK dy rfH dq^^^ dq dq dq ^ Ainsi auf der Aura à la Surface du corps Ã © l

. Denkschriften der Kaiserlichen Akademie, Christian/Mathematisch-Naturwissenschaftliche Classe. Mathematik, Wissenschaft. Allgemeine Transformation der bestimmten Doppel-Integrale. 155 dann b als positiv, so wird man nach einigen sich leicht anbietenden Reductionen sterben folgende Gleichung erhalten: Ich dx ff (ax'" von") dy=/tÃ¤7 H) - ir-r (-+-) m n i ttpÂ " ", "âf "4 // "âaf n â * w4 - âL-j.zm+n * f{z) dz I{âtf lt w*> dtA-/zm +7'lÃr-z) dzJ (lât) m'Â"' - + "'* j Macht man sterben noch speciellere Annahme, dass Â £ = oo, jy = oo sei, so wird der Mensch haben: O * CO fdx ff (a Stockfoto

RMRD0TK7–. Denkschriften der Kaiserlichen Akademie, Christian/Mathematisch-Naturwissenschaftliche Classe. Mathematik, Wissenschaft. Allgemeine Transformation der bestimmten Doppel-Integrale. 155 dann b als positiv, so wird man nach einigen sich leicht anbietenden Reductionen sterben folgende Gleichung erhalten: Ich dx ff (ax'" von") dy=/tÃ¤7 H) - ir-r (-+-) m n i ttpÂ " ", "âf "4 // "âaf n â * w4 - âL-j.zm+n * f{z) dz I{âtf lt w*> dtA-/zm +7'lÃr-z) dzJ (lât) m'Â"' - + "'* j Macht man sterben noch speciellere Annahme, dass Â £ = oo, jy = oo sei, so wird der Mensch haben: O * CO fdx ff (a

Dy dx Stockfotos & Bilder

Dy dx Stockfotos & Bilder

Download-Bestätigung

Passwortbestätigung

Suchergebnisse für Dy dx Stock-Fotos & Bilder (157)

Nach Kollektionen der Agentur filtern

Suchmanager

Erhalten Sie großartige Funktionen mit Ihrem kostenlosen Konto

Lass dich für dein nächstes Projekt inspirieren!